Aunque históricamente el primer trabajo de Álgebra Lineal consistió en resolver sistemas de m ecuaciones lineales con n incógnitas, comenzaremos este curso estudiando la estructura de espacio vectorial.
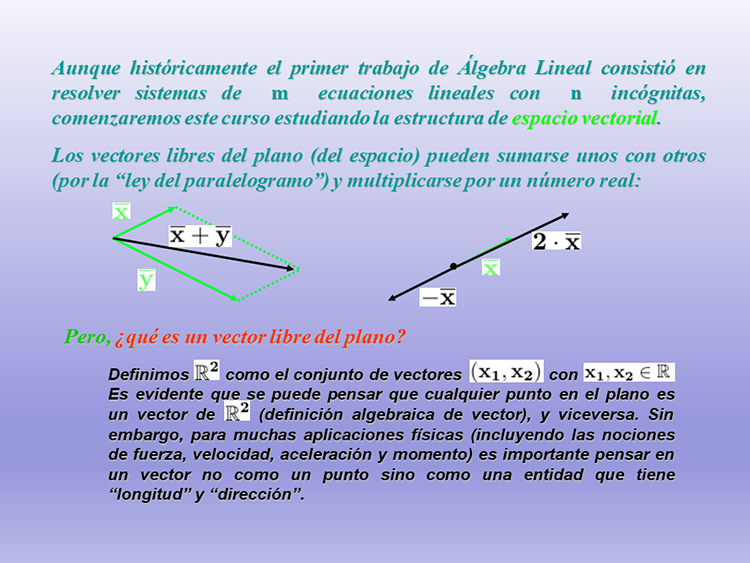
Los vectores libres del plano (del espacio) pueden sumarse unos con otros (por la “ley del paralelogramo”) y multiplicarse por un número real:
Pero, ¿qué es un vector libre del plano?
Definimos como el conjunto de vectores con . Es evidente que se puede pensar que cualquier punto en el plano es un vector de (definición algebraica de vector), y viceversa. Sin embargo, para muchas aplicaciones físicas (incluyendo las nociones de fuerza, velocidad, aceleración y momento) es importante pensar en un vector no como un punto sino como una entidad que tiene “longitud” y “dirección”.

Tanto en Física como en Ingeniería un vector se caracteriza por dos magnitudes (longitud y dirección) y se representa por un segmento recto dirigido. Un vector en el plano puede ubicarse en diferentes lugares. Sin embargo, con independencia de dónde esté situado, si la longitud y dirección no varían se trata del mismo vector.
El conjunto de los vectores libres del plano ( ) es sólo un ejemplo entre los muchos ejemplos de objetos matemáticos que pueden sumarse entre sí y multiplicarse por números reales, y que además satisfacen unas mismas propiedades. Este ejemplo de los vectores libres del plano (o el de los vectores libres del espacio) es importante porque su representación geométrica ayuda a entender la definición general de vector.

Algunos ejemplos que podemos mencionar son:
los propios números reales,
los números complejos,
los vectores en el plano,
los vectores en el espacio,
los polinomios de grado menor o igual que n,
las funciones reales de variable real con dominio D,
las funciones continuas en un intervalo,
las funciones derivables en un punto,
las funciones integrables en un intervalo,
……………………………….
Un vector puede ser un número, una n-tupla, un polinomio, una función continua, etc.

También hay magnitudes físicas de tipo vectorial con las mismas propiedades: fuerzas, velocidades, aceleraciones,….
Cuando en varios conjuntos distintos aparecen estructuras similares, es conveniente axiomatizar éstas y dar un nombre al ente resultante. Aunque este primer tema tiene el inconveniente de trabajar en el mundo abstracto de los espacios vectoriales arbitrarios, también presenta una gran ventaja. La abstracción resulta ser matemáticamente eficiente en el sentido de que ahora pueden demostrarse resultados generales cuya validez afecta a todos los espacios vectoriales. Es decir, una vez que se establecen los hechos sobre los espacios vectoriales en general, se pueden aplicar estos hechos a todos los espacios vectoriales. De otro modo, habría que probar cada hecho una y otra vez, para cada nuevo espacio vectorial que nos encontráramos (y existen un sin fin de ellos).

En este curso, básicamente trabajaremos con cuatro espacios vectoriales.
En el tema 1 definimos la estructura de espacio vectorial y trabajaremos con los espacios vectoriales siguientes:
En el tema 2 estudiamos el espacio vectorial de las matrices reales de m filas y n columnas, que denotamos:
Por último, en el tema 6 trabajaremos también con espacios vectoriales de funciones reales de variable real y continuas sobre un intervalo.
A continuación, presentamos un ejemplo introductorio que proporciona una motivación para desarrollar las matemáticas subsecuentes.
, normalmente n=3 o n=4.
, normalmente n=2 o n=3.

Un poco de historia
El matemático alemán Grassmann es reconocido como el primero que introdujo la idea de un espacio vectorial (aunque no lo llamó de esta manera, sino sistema de números hipercomplejos) y de independencia lineal en 1844. Desafortunadamente su trabajo era muy difícil de leer y no recibió la atención que merecía.
Peano en su libro Calcolo geometrico (1898) acalaró el trabajo de Grassmann y estableció los axiomas de espacio vectorial como los conocemos en la actualidad. En este mismo libro introdujo las operaciones de conjuntos. Sus notaciones ?, ? y ? son las que todavía utilizamos, aunque no fueron aceptadas de inmediato. La definición axiomática de Peano de un espacio vectorial también tuvo muy poca influencia durante muchos años. Su aceptación se produjo en 1918, después de que Hermann Weyl la repitiera en su libro Space, time, matter, una introducción a la teoría de la relatividad general de Einstein.
También podemos mencionar a William R. Hamilton, que durante los veinte últimos años de su vida, dedicó la mayor parte de su creación matemática a desarrollar la tería de un tipo especial de números, los cuaterniones. Con estos trabajos cimentó la moderna noción de vector. Todavía hoy se utiliza la notación i, j, k de Hamilton para los vectores de la base canónica en el espacio tridimensional.

ESTRUCTURA DE ESPACIO VECTORIAL REAL
Sean (cjto. números reales) y
operación interna en V
operación externa en V con dominio de operadores
Definiremos cuando V es un espacio vectorial real

Como hemos visto, partimos de un conjunto no vacío V , cuyos elementos se denotan …, y se denominan vectores y del cuerpo conmutativo (estructura algebraica) de los números reales. En general se puede trabajar con cualquier cuerpo conmutativo K y en este curso surgirán algunos ejercicios con espacios vectoriales complejos ( K= ).
La ley de composición interna se suele denotar con el símbolo de la suma ( ? ) y se suele denominar suma de vectores. Es una aplicación que a cada par de elementos de V les hace corresponder el elemento, también de V, , denominado suma de e .
La ley de composición externa con dominio de operadores (en general, con dominio de operadores K) es una aplicación que denominamos producto por un escalar y denotamos con el símbolo del producto ( ? ) que a todo elemento de V y a todo elemento ? de (o K) hace corresponder el elemento .
OBSERVACIÓN.- ¿Es la suma de polinomios una ley de composición interna sobre el conjunto de los polinomios de grado exactamente 2?

ESTRUCTURA DE ESPACIO VECTORIAL
.- Para ( + ) (operación interna) se cumple:
.- Para ( • ) (op. externa con dominio ) se cumple:

Los elementos de un espacio vectorial reciben el nombre genérico de vectores y en general se utiliza la notación vectorial ( ,…) para denotarlos. Esto no es obstáculo para que en algunos casos particulares (polinomios, matrices, funciones,…) se utilice la notación propia en cada caso.
Los axiomas 1.- de la definición de espacio vectorial real se refieren a la suma de vectores, los axiomas 2.- c.- y 2.- d.- se refieren exclusivamente a la multiplicación por escalares (números reales) y las propiedades 2.- a.- y 2.- b.- son las propiedades distributivas de una operación con respecto a otra.
A continuación presentamos varios ejemplos de espacios vectoriales. Para comprobar que tienen estructura de espacio vectorial deberíamos ver que se satisfacen los 8 axiomas de la definición con las operaciones suma y producto por un escalar definidas. Este trabajo es muy sencillo y se basa exclusivamente en propiedades de los números reales (no olvidar que estamos trabajando, en principio, con espacios vectoriales reales). Dado que también es una labor muy tediosa omitiremos las comprobaciones, pero hay que insistir en que es absolutamente necesario comprobar los 8 axiomas.

EJEMPLOS DE ESPACIOS VECTORIALES
-EJEMPLO 1.-
conjunto de los vectores libres del espacio
¿Cómo se suman dos vectores libres?
¿Cómo se multiplica un vector por un número real?
¿Cuál es el vector nulo?

-EJEMPLO 2.-
¿Cómo se suman dos vectores libres?
¿Cómo se multiplica un vector por un número real?
¿Cuál es el vector nulo?
Página siguiente  |