
En esta UNIDAD comenzamos a introducirnos en los:
MÉTODOS NUMÉRICOS
Situación REAL NO SIEMPRE se requiere una RESPUESTA EXACTA
MODELO MATEMÁTICO para describir y analizar
APROXIMACIÓN
SOLUCIÓN ANALÍTICA: Puede NO tener
Puede ser DIFÍCIL o COSTOSA (objetivos)
MÉTODOS NUMÉRICOS
Una SOLUCIÓN APROXIMADA al PROBLEMA ORIGINAL
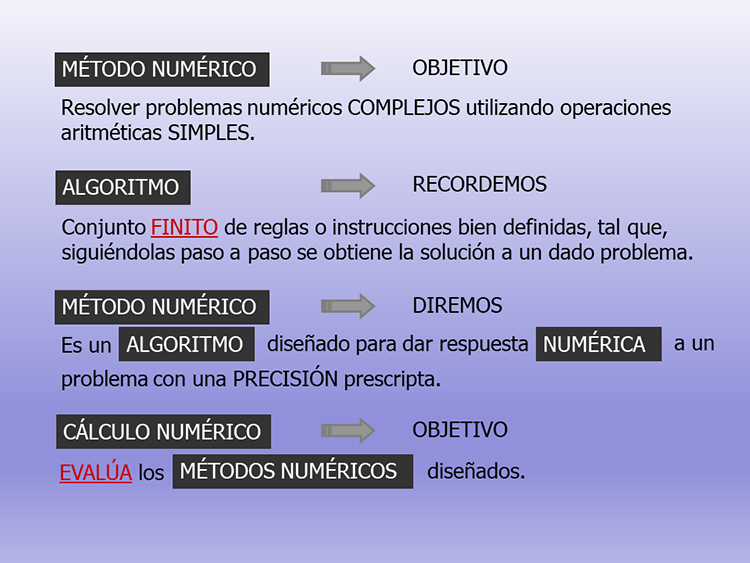
MÉTODO NUMÉRICO
Resolver problemas numéricos COMPLEJOS utilizando operaciones aritméticas SIMPLES.
OBJETIVO
(Gp:) Conjunto FINITO de reglas o instrucciones bien definidas, tal que, siguiéndolas paso a paso se obtiene la solución a un dado problema.
(Gp:) ALGORITMO
(Gp:) RECORDEMOS
(Gp:) MÉTODO NUMÉRICO
(Gp:) Es un
(Gp:) ALGORITMO
(Gp:) diseñado para dar respuesta
(Gp:) problema con una PRECISIÓN prescripta.
(Gp:) NUMÉRICA
(Gp:) a un
(Gp:) DIREMOS
(Gp:) CÁLCULO NUMÉRICO
(Gp:) EVALÚA los
(Gp:) MÉTODOS NUMÉRICOS
(Gp:) diseñados.
(Gp:) OBJETIVO

El CÁLCULO de un dado MÉTODO NUMÉRICO dará NÚMEROS que se APROXIMAN a los que se obtendrían aplicando la SOLUCIÓN ANALÍTICA de un problema, en el caso que existiera.
DIREMOS
¿Qué tan PRECISOS (próximos a la solución “exacta”) son los resultados?
O
¿Qué tanto ERROR se ha introducido?
(Gp:) NOS PREGUNTAMOS
(Gp:) Si el cálculo aproxima a la solución “exacta”:
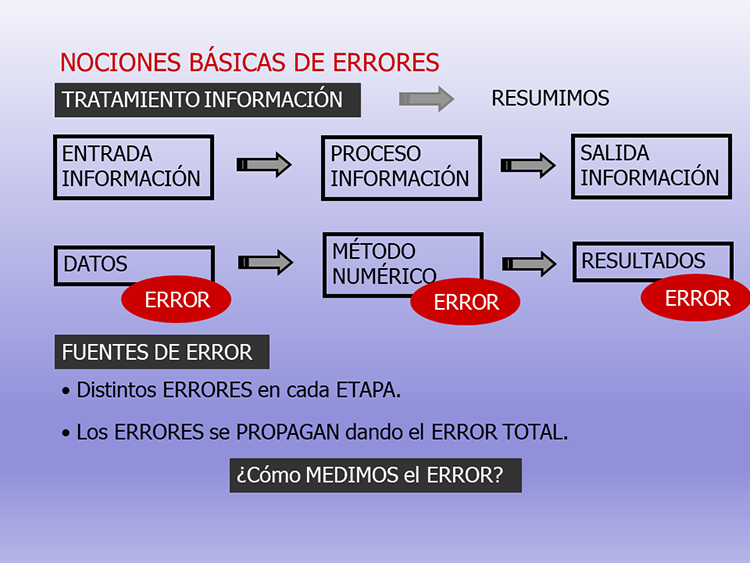
(Gp:) TRATAMIENTO INFORMACIÓN
(Gp:) RESUMIMOS
(Gp:) ENTRADA
INFORMACIÓN
(Gp:) PROCESO
INFORMACIÓN
(Gp:) SALIDA
INFORMACIÓN
NOCIONES BÁSICAS DE ERRORES
(Gp:) DATOS
(Gp:) MÉTODO NUMÉRICO
(Gp:) RESULTADOS
FUENTES DE ERROR
Distintos ERRORES en cada ETAPA.
(Gp:) ERROR
(Gp:) ERROR
(Gp:) ERROR
Los ERRORES se PROPAGAN dando el ERROR TOTAL.
¿Cómo MEDIMOS el ERROR?

MAGNITUD DEL ERROR
CUANTIFICAMOS el ERROR:
Siendo VA una aproximación de VV, y VV el valor real, entonces:
e = | VA – VV |
eR = | ( VA – VV ) / VV | con la condición VV ? 0
ERROR PORCENTUAL ABSOLUTO
ERROR ABSOLUTO
ERROR RELATIVO ABSOLUTO
eP = 100.| ( VA – VV ) / VV |(%) con la condición VV ? 0

CIFRAS SIGNIFICATIVAS
EJEMPLOS
MEDIR la CONFIABILIDAD de un VALOR NUMÉRICO
(Gp:) Siendo VA una aproximación de VV (de la definición de ERROR RELATIVO)
(Gp:)
Si d es el mayor número natural tal que | ( VA – VV ) / VV | < 10-d/2
VA es una aproximación a VV con d CIFRAS SIGNIFICATIVAS
(Gp:) VA = 3.14 y VV = 3.141592 ?
(Gp:) |(VA – VV)/VV| = 0.000507 < 10-2/2
VA es una aproximación a VV con 2 cifras significativas.
(Gp:) VA = 999 996 y VV = 1 000 000 ?
(Gp:) |(VA – VV)/VV| = 0.000004 < 10-5/2
VA es una aproximación a VV con 5 cifras significativas.
(Gp:) VA = 0.000012 y VV = 0.000009 ?
(Gp:) |(VA – VV)/VV| = 0.25 < 10-0/2
VA es una aproximación a VV con 0 cifras significativas.

(Gp:) PROCESO
(Gp:) MÉTODO NUMÉRICO
(Gp:) ALGORITMO COMPUTACIONAL
FUENTES DE ERROR
ERRORES
ERROR DE TRUNCAMIENTO (tiempo).
(Gp:) Tiempo
ERROR DE REDONDEO (espacio).
ERRORES en el CÁLCULO al implementar en MÁQUINA el MÉTODO.
Es decir:
TIEMPO FINITO (ALGORITMO)
ESPACIO FINITO (COMPUTADORA)
(Gp:) INTENCIONALMENTE al usar un ALGORITMO COMPUTACIONAL
(Gp:) Introducimos restricciones:
(Gp:) Espacio
RIGUROSAMENTE: FINITO no alcanza. FINITO debe entenderse como RAZONABLE.

FUENTES DE ERROR EN EL ALGORITMO COMPUTACIONAL
ERROR DE TRUNCAMIENTO
SURGEN debido a la limitación en TIEMPO.
Debemos realizar un número finito de acciones.
EJEMPLOS:
Evaluar funciones con la Serie de Taylor.
Proceso iterativo convergente.
Evaluar por intervalos.
Faltará evaluar (ERROR) términos, iteraciones o intervalos TRUNCADOS.
NO PODEMOS IMPLEMENTAR EL LÍMITE ANALÍTICO
TRUNCAR

FUENTES DE ERROR EN EL ALGORITMO COMPUTACIONAL
ERROR DE REDONDEO
SURGEN debido a la limitación en ESPACIO (la memoria ocupa espacio).
Los números reales se representan por una INFINIDAD de dígitos.
En MÁQUINA sólo podemos tener un representación FINITA.
X = ± 0, d1 d2 d3 …. dm x 10n , 1=d1=9 y 0=di=9
d1 d2 d3 …. dm: mantisa n: exponente
Trabajamos con: fl(x) = ± 0, d1 d2 d3 …. dk x 10n
Tenemos almacenado un REDONDEO del número real que difiere (ERROR) del número real.

El redondeo truncado consiste en truncar el resultado de una operación al número de cifras significativas que se estén utilizando. Por ejemplo sí redondeamos 7/9 a 4 cifras significativas tenemos 0.7777
Errores
REDONDEO TRUNCADO
REDONDEO SIMÉTRICO
El redondeo simétrico consiste en aumentar en uno la última cifra retenida si la primera cifra descartada está entre 5 y 9, o dejarla igual si la primera cifra descartada está entre 0 y 4.
Ejemplo: 1/3 + 2/3 = 1, su resolución mediante la calculadora puede llevarnos a un resultado diferente. Si realizamos la suma empleando únicamente 4 cifras significativas se obtiene

ERROR NUMÉRICO TOTAL
ERROR NUMÉRICO TOTAL
Agregando términos, iteraciones o disminuyendo el intervalo.
DISMINUIR UNA COMPONENTE DE ERROR CONDUCE A UN INCREMENTO EN LA OTRA
ERROR DE TRUNCAMIENTO
ERROR DE REDONDEO
Error de truncamiento
Significa
número de operaciones
Error de redondeo

There are 10 types of people in the world:
those who understand binary
and
those who don't.
2
Página siguiente  |