
ESTRUCTURA DE LA MATERIA I
Dualidad onda-corpúsculo. Ondas de De Broglie. Efecto Compton. Difracción de electrones.
Teoría de la radiación de Planck. Cuantos de energía. Efecto Fotoeléctrico: Teoría de Einstein.
Interpretación ondulatoria del movimiento de las partículas. Teoría cuántica de Schrödinger. Interpretación física de la función de onda asociada a una partícula. Probabilidad e incertidumbre.
Niveles de energía en sistemas cuánticos. Pozos y barreras de potencial unidimensionales.

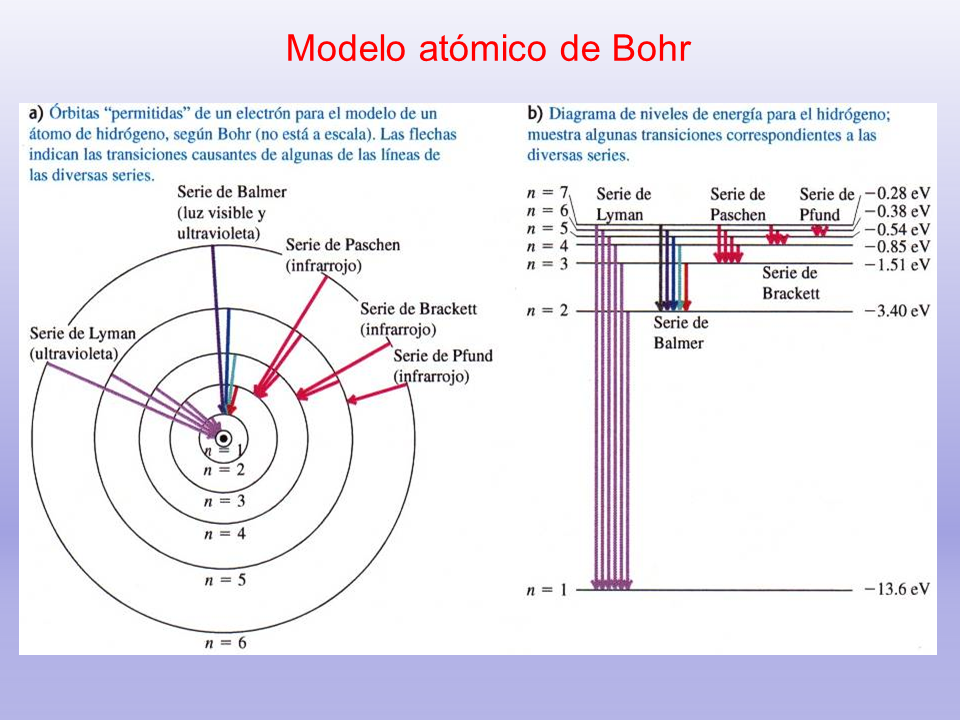
Modelo atómico de Bohr
1. Los electrones orbitan el átomo en niveles discretos y cuantizados de energía, es decir, no todas las órbitas están permitidas, tan sólo un número finito de éstas.
2. Los electrones pueden saltar de un nivel electrónico a otro sin pasar por estados intermedios.
3. El salto de un electrón de un nivel cuántico a otro implica la emisión o absorción de un único cuanto de luz (fotón) cuya energía corresponde a la diferencia de energía entre ambas órbitas.
4.Las órbitas permitidas tienen valores discretos o cuantizados del momento angular orbital L de acuerdo con la siguiente ecuación: L = n h = n (h/ 2p)
Donde n = 1,2,3,… es el número cuántico angular o número cuántico principal.
La cuarta hipótesis asume que el valor mínimo
de n es 1. Este valor corresponde a un mínimo
radio de la órbita del electrón de 0.0529 nm.
A esta distancia se le denomina radio de Bohr.
Un electrón en este nivel fundamental no puede
descender a niveles inferiores emitiendo energía.
Modelo atómico de Bohr

Sub De acuerdo con la física clásica existen diferencias entre onda y partícula. Una partícula ocupa un lugar en el espacio y tiene masa mientras que una onda se extiende en el espacio caracterizándose por tener una velocidad definida y masa nula
Ondas de De Broglie
De Broglie dijo: “La luz es dual en su naturaleza: onda y partícula” Su trabajo decía que la longitud de onda, ?, de la onda asociada a la partícula era
donde h es la constante de Planck y p es la cantidad de movimiento de la partícula

Efecto Compton

Principio de incertidumbre de Heisenberg
Esta doble condición electrónica de onda y corpúsculo ocasionó un problema sobre la posición del mismo, ya que no tiene demasiado sentido hablar de la posición de una onda. “Es imposible conocer simultáneamente la posición y la cantidad de movimiento de una partícula”.
Así: ?x . ?p = h / 4p
siendo ?x la incertidumbre en la posición y ?p la incertidumbre en la cantidad de movimiento.
De esta manera, la idea de órbita perfectamente definida se sustituye por la idea de orbital que sería la zona del espacio alrededor del núcleo atómico en donde existiría la máxima probabilidad de encontrar un electrón. El orbital, pues, no tiene límites perfectamente definidos.

Efecto fotoelectrico
Todos los fenómenos apuntaban a la naturaleza cuántica de la radiación. La radiación electromagnética tiene propiedades que se asemejan a una partícula y la energía asociada se emite y se absorbe en forma de fotones o cuantos cuya energía es proporcional a la frecuencia de la radiación.
El efecto fotoeléctrico es la emisión de electrones cuando la luz choca contra una superficie. Fue observado por primera vez por Hertz .

Ecuación de Schrödinger unidimensional
La función de onda para una partícula en una caja tiene la forma
La energía del nivel correspondiente se expresa como (p=h/? y ?=2?/k)
Atención: la derivada segunda de ? multiplicada por –h2/8 ?2m es lo mismo que multiplicar ? por el factor (-h2 k2/ 8?2m)(-k2) que es E
De tal forma que queda
Que es la forma más simple de la ecuación de Schrödinger

Variantes de esta ecuación:
Función de onda dependiente del tiempo, estado estacionario
? (x,t) = ? (x) e-i(2? E / h) t
Ecuación de Schrödinger unidimensional de una partícula sobre la que actua una fuerza
La solución general de la ecuación de Schrodinger conduce a una serie de niveles de energía caracterizados por un número cuántico n.

Oscilador armónico cuántico. Ecuación de Schrodinger

Niveles de energía en sistemas cuánticos. Pozos y barreras de potencial unidimensionales
Potencial de pozo cuadrado
(Gp:) U(x)
(Gp:) 0
(Gp:) L
(Gp:) 0 a
(Gp:) x
(Gp:) E1
(Gp:) E2
(Gp:) U(x)
Barrera de Potencial
Efecto túnel
Según la mecánica cuántica, los electrones no están definidos por una posición precisa, sino por una nube de probabilidad. Esto provoca que en ciertos sistemas esta nube de probabilidad se extienda hasta el otro lado de una barrera de potencial. Por tanto el electrón puede atravesar la barrera, y contribuir a generar una intensidad eléctrica

Efecto tunel
Función de onda para una partícula que atraviesa una barrera de potencial

ESTRUCTURA DE LA MATERIA II
Introducción a la teoría cuántica del átomo. Niveles de energía y números cuánticos. Transiciones entre niveles de energía. Series espectrales y espectros.
Descripción cuántica de la estructura de sólidos. Bandas de energía. Propiedades derivadas de la estructura de bandas: metales, semiconductores y aislantes.
Nucleo atómico. Tipos de núcleos. Isótopos.
Estabilidad relativa de los nucleos. Radiactividad y otros procesos nucleares naturales. Emisiones alfa, beta y gamma. Series radiactivas.
Reacciones nucleares. Fisión y fusión nuclear.
Interacciones fundamentales en la naturaleza. Partículas fundamentales. Leyes de conservación. Modelo standard.

Introducción a la teoría cuántica del átomo. Niveles de energía y números cuánticos. Transiciones entre niveles de energía. Series espectrales y espectros
La aplicación de la ecuación de Schrödinger en coordenadas esféricas (r, ?, ?) al átomo de Hidrógeno usando un valor de energía potencial
se puede resolver de forma exacta. La función de onda ? (r, ?, ? ) se puede expresar como el producto de tres funciones donde cada una es función de una coordenada.
Solución:
Siendo n el nº cuántico principal

Para que la ecuación de Schrödinger tenga significado físico es necesario imponerle unas restricciones que son conocidas como números cuánticos:
n:nº cuantico principal
l: nº cuántico del momento angular orbital
m: nº cuántico magnético
s: nº cuántico del spin electronico
Estos números cuánticos sólo pueden tomar ciertos valores permitidos
n: números enteros 1,2,3
l: números enteros desde o hasta (n-1)
m: números enteros entre +1 y -1 incluido 0
S: números fraccionarios -1/2 y +1/2

Series espectrales
Página siguiente  |