
Funciones Potencias
Se llama función potencia a cualquier expresión que se pueda escribir de la forma:
Son funciones potencias: x2, x-1 , x1/2
Con a cualquier número real.

Gráfica de
Funciones Potencias
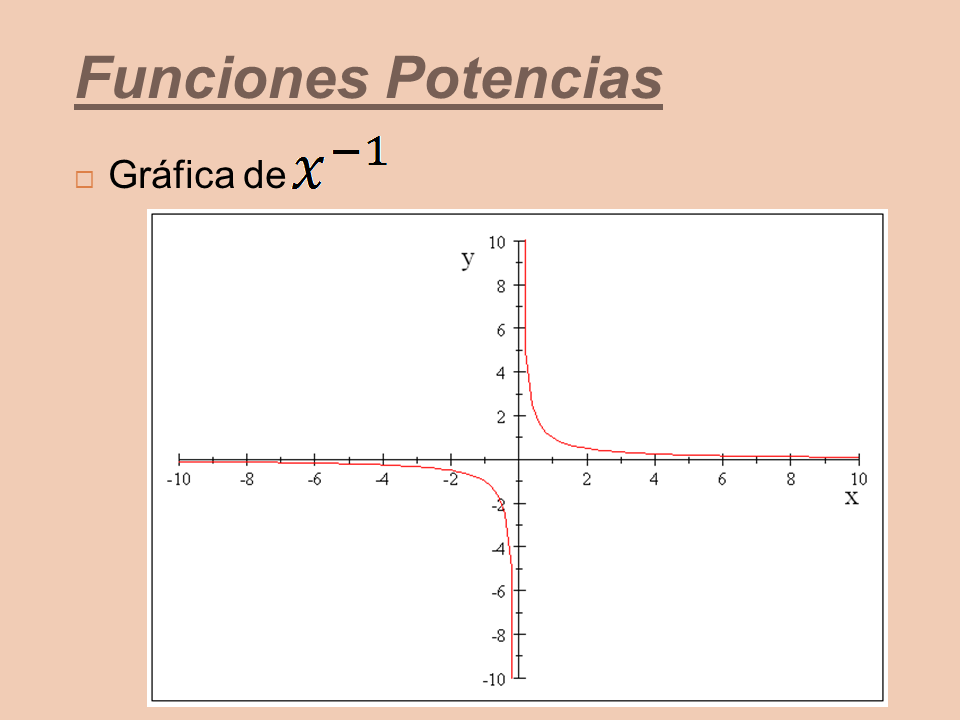
Gráfica de
Funciones Potencias

Gráfica de
Funciones Potencias
x1/2

Dilatación y Contracción
Un dato importante para recordar es que mientras más grande sea el valor de a, la gráfica de la función más cerca del eje y se encontrará, y mientras más pequeño sea este valor más lejos del eje y se encontrará, es decir:
Funciones Potencias

Realizar las siguientes gráficas.
Funciones Potencias

Funciones Exponenciales.
Se llama función exponencial de base a, a>0, a la función de la forma:
También lo podemos escribir como:
Ejemplos:

Gráfica de 2x
Funciones Exponenciales.

Funciones Exponenciales.
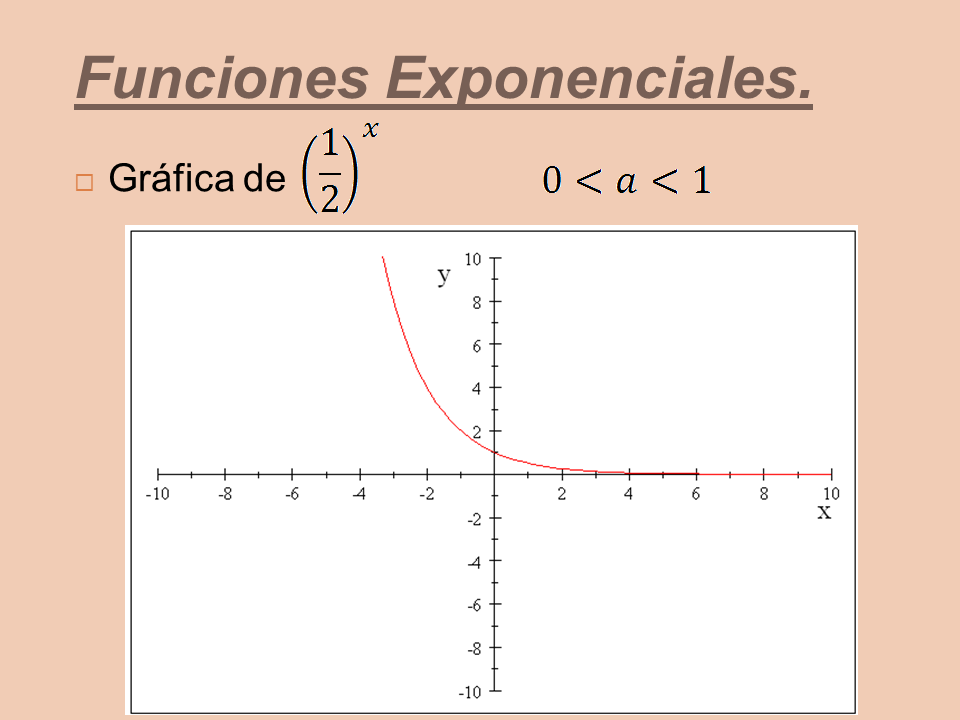
Gráfica de
Funciones Exponenciales.

Funciones Exponenciales.

Gráfica de
Funciones Exponenciales.

Gráfica de 8x
Funciones Exponenciales.

Ecuaciones Exponenciales.
Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente.
Para resolver una ecuación exponencial vamos a tener en cuenta:

Propiedades a considerar.
Ecuaciones Exponenciales.

Resuelva.
Ecuaciones Exponenciales.
Página siguiente  |