El Mundo de la Óptica (página 3)

Partes: 1, 2, 3, 4

REFRACCIÓN DE LA LUZ: La ley de Snell
También suele escribirse en función da las rapideces que lleva la luz en los medios en cuestión

ALGUNOS ÍNDICES ABSOLUTOS DE REFRACCIÓN …
(Gp:) SUSTANCIA
(Gp:) ?
(Gp:) Aire
(Gp:) Agua
(Gp:) Alcohol Etílico
(Gp:) Hielo
(Gp:) Sal común
(Gp:) Diamante
(Gp:) Vidrio crown ligero
(Gp:) Benceno
(Gp:) 1
(Gp:) 1.3333
(Gp:) 1,354
(Gp:) 1,31
(Gp:) 1,544
(Gp:) 2,427
(Gp:) 1,515
(Gp:) 1,501

EJEMPLO
1.- Se hizo pasar luz por un material desconocido. La luz que inicialmente se propagaba en el aire incidió con un ángulo de 30° y se refractó con ángulo de 19°. Determinar:
a) índice de refracción del material
Aplicando la ley de Snell, se tiene que:
n1 sen ?1= n2 sen ?2
1 sen 30º = n2 sen 19º
n2 = 1,535

b) Rapidez de propagación de la luz en ese medio
Para determinar la rapidez de la luz en ese medio aplicamos la ecuación ? = c/v.
1,535 = 300.000 / v
V = 195.439,7 km/s

POSIBILIDADES DE REFRACCIÓN
A partir de la ley de Snell se puede predecir la forma en que debe refractarse la luz. Esto dependerá de los valores de los índices de refracción absolutos de los medios y del ángulo de incidencia. En general, si no incide perpendicularmente se tiene dos posibilidades:
(Gp:) ?1
(Gp:) ?2

?1< ?2
?1> ?2
(Gp:) ?1
(Gp:) ?2

UN CASO ESPECIAL DE REFRACCIÓN DE LA LUZ
Un caso especial es cuando el ángulo de incidencia es 90°. En tal caso el rayo transmitido no sufre desviación, pero si modifica su rapidez y longitud de onda.

?1
?2

ÍNDICE DE REFRACCIÓN Y LONGITUD DE ONDA
De la definición de índice de refracción relativo podemos determinar una relación matemática entre la longitud de onda y los respectivos índices de refracción de los medios. Como ?1/ ?2 = v2 / v1 se cumple que:
?1/ ?2 = ?2f / ?1f
?1/?2 = ?2 / ?1

PERCEPCIÓN DE LAPROFUNDIDAD
Cuando la luz se refracta, puede ocasionar fenómenos que se relación con la posición aparente de las cosas. Un objeto sumergido en el fondo de un estanque, es visto en la posición “P” por un observador “O” ubicado una cierta distancia de él.

Análisis matemático
da
do
s
?1
?2
tan ?1 = s / da y tan ?2 = s / do
da tan ?1 = d0 tan ?2
da = (tan ?2 / tan ?1) do
Si consideramos la refracción para ángulos pequeños ( ?? 15º), el cos ?? 1. Luego tan ? = sen ?/ cos? ? sen?. Así la expresión para da queda : da= ( sen?2 / sen ?1 ) do . .Aplicando la ley de Snell se cumple que:sen?2 / sen ?1= ?2 / ?1 , o sea, sen?2 / sen ?1= 1 / ?1.Finalmente y reemplazando se tiene que:
?2
?1
da = do / n1
n1
n2

REFLEXIÓN TOTAL INTERNA
Cuando un haz luminoso incide de un medio de índice ?1 a otro con índice ?2 tal que ?1> ?2 el rayo refractado se aleja de la normal. Si el ángulo de incidencia aumenta, también lo hace el de refracción, de modo tal que se cumpla la ley de Snell ( ?1sen?1= ?2 sen ?2)

(Gp:) ?3
(Gp:) ?4

?1
?2

REFLEXIÓN TOTAL INTERNA
La situación se hace crítica cuando el ángulo de incidencia es tal que el ángulo de refracción es 90º. En la figura ? representa el ángulo crítico para dos medios cualesquiera. Aplicando la ley de Snell es fácil demostrar que el ángulo crítico para un par de medio es:

? = arc sen ?2 / ?1
(Gp:) ?
(Gp:) ?
(Gp:) ?2
(Gp:) ?1

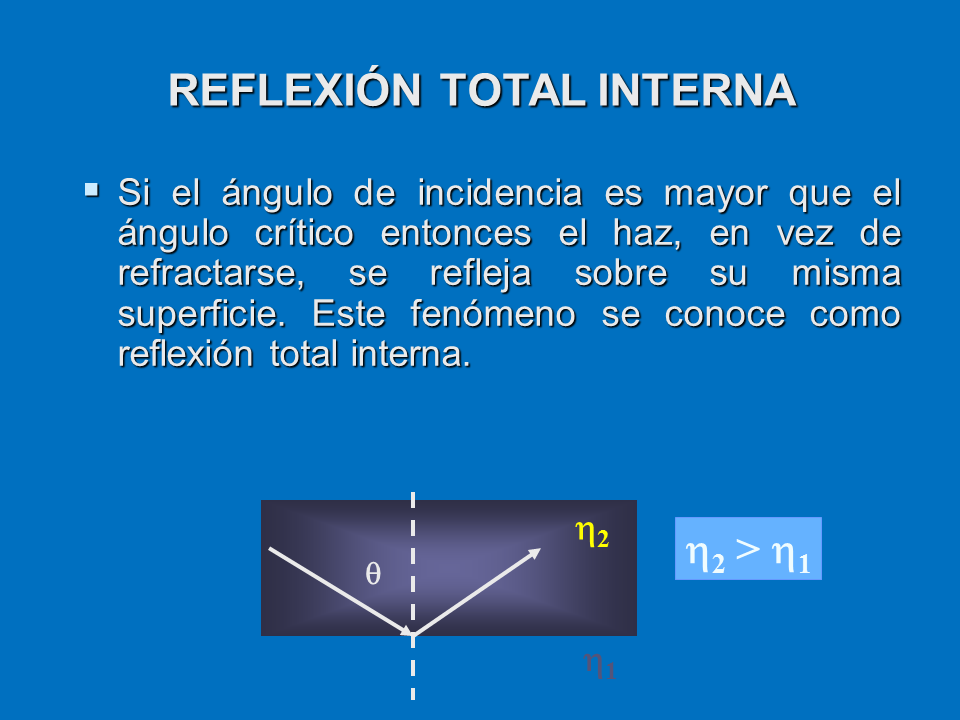
REFLEXIÓN TOTAL INTERNA
Si el ángulo de incidencia es mayor que el ángulo crítico entonces el haz, en vez de refractarse, se refleja sobre su misma superficie. Este fenómeno se conoce como reflexión total interna.

?
?2
?1
?2 > ?1

REFLEXIÓN, REFRACCIÓN y TRANSMISIÓN: fenómenos muy comunes
El fenómeno de la refracción generalmente está acompañado de otros fenómenos observables. Uno de ellos se refiere a que parte de la luz incidente es reflejada por el medio respectivo. Así, del 100% de la energía que incide parte es devuelta al medio de procedencia. La porción reflejada dependerá de las características del medio transparente.
(Gp:) Onda incidente
(Gp:) Onda reflejada
(Gp:) Onda refractada

LENTES: Instrumentos de grandes usos tecnológicos
Son cuerpos que permiten el paso de la luz y que producto de la refracción de ella, permiten obtener imágenes con ciertas características dependiendo del tipo de lente que se use. Así, las lentes pueden clasificarse en: convergentes y divergentes.

Lente divergente
Lente convergente
Los rayos refractados se separan
Los rayos refractados se reúnen

ELEMENTOS PRINCIPALES de las lentes
En toda lente podemos distinguir los siguientes elementos principales: Dos centros de curvatura ( C ), dos radios de curvatura ( r) , un eje principal, dos focos ( F ), y un centro óptico ( O ).

(Gp:) C
(Gp:) C
(Gp:) r
(Gp:) r
(Gp:) O
(Gp:) Eje
principal

(Gp:) O
(Gp:) C
(Gp:) C
(Gp:) r
(Gp:) r
(Gp:) Eje
principal

F
F
F
F

TIPOS DE LENTES de acuerdo a su convergencia o divergencia

TIPOS DE LENTESde acuerdo a su convergencia o divergencia

CONSTRUCCIÓN DE IMÁGENESlentes convergente y divergente
Aquí se distinguen los siguientes: Aquel que viaja paralelo al eje y se refracta pasando por el foco, el incide sobre el centro sin sufrir desviación, el que pasa por el foco y se refracta paralelo al eje. Con dos de ellos es suficiente para construir la imagen

CONSTRUCCIÓN DE IMÁGENESlentes convergente
Objeto entre el infinito y dos veces la distancia focal
Imagen real-invertida-igual tamaño
Objeto entre dos veces la distancia focal y la distancia focal
Imagen real-invertida-mayor tamaño

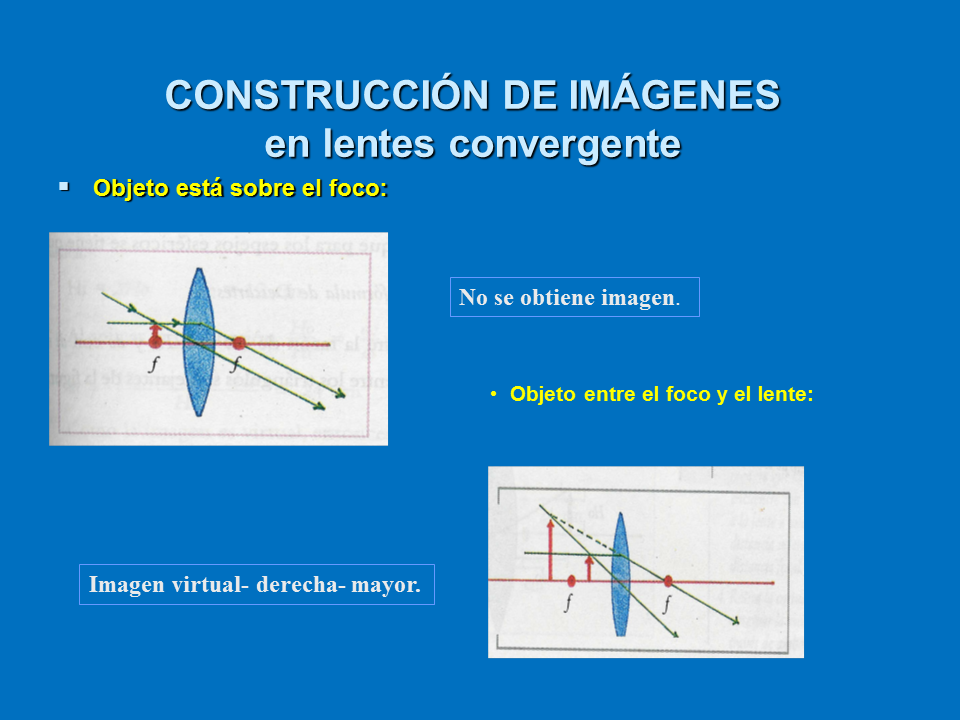
CONSTRUCCIÓN DE IMÁGENESen lentes convergente
Objeto está sobre el foco:
No se obtiene imagen.
Objeto entre el foco y el lente:
Imagen virtual- derecha- mayor.