
FISICA I
Informe de Practica de Laboratorio Nº 1
LINEALIZACION
Grupo “A”
Docente: Ing. Cesar Gutiérrez
Integrantes:
Rodríguez Lazarte Fabio Alexis
Cochabamba 5 de septiembre del 2016
Gestión Il – 2016

2) Competencias:
Conocer el ajuste de curvas potencial, exponencial y regresión lineal para su aplicación en las diversas
prácticas de laboratorio
Conocer el ajuste de curvas potencial, exponencial y regresión lineal para su aplicación en las diversas
prácticas de laboratorio
3) Materiales:
Hoja de papel milimetrado
Calculadora científica
Lápiz
Estuche geométrico
4) Procedimiento:
I.
II.
Graficar los datos (pares ordenados) proporcionados en la guía práctica en una hoja milimetrada.
Una vez graficado los pares ordenados aproximar linealmente a una función (linealizar), y si tenemos un
diagrama de dispersión parecido al de una recta aplicar directamente regresión lineal, si la gráfica no es
una recta del tipo (y=ax +b), y tenemos una tipo (y=b
o y=b
) linealizar aplicando la técnica de
III.
IV.
V.
logaritmación, y después determinar parámetros a y b por el método de mínimos cuadrados.
Encontrar la ecuación empírica del diagrama de dispersión.
Encontrar el coeficiente de correlación.
Graficar el resultado de la ecuación hallada
5) cálculos y resultados:
Experimento 1) la siguiente tabla de datos se obtuvo de un experimento de movimiento uniformemente acelerado,
el experimento se realizó partiendo de reposo, la ecuación teórica es:
X=0.5a
X= a

a =10
Logx=log +2logt
Logx=Y
A=
X= logt
B= log a
b=10
Y=Ax+B
y=b
A=
?
?
?
?
?
=
B=
?
?
A=
* .
,
,
* .
!
,
"
= 1.075217167
y=1.08x+1.55
y=10
y=36.21679
#.$%
B=
R=
,
& ?
?
?
,
? ?
*& ?
?
= 1.558911792
=
#$*#.#%%$ '( ) $,$$$** #+,+*$##$#
R=
&#$*#.#$,)%$ ) $,$$$** )#* *&#$* +.%) *)(''
#+,+*$##$#
= 0, 9108

& ?
Experimento 2) se realizó un experimento de movimiento rectilíneo uniformemente acelerado y los datos
obtenidos fueron:
y=B-./
lny=lnB+Axlne
lny=lnB+Ax
y= lny
B= lnb
Ax=Ax
b=-
Y=Ax+B
y=b-
/
a=
?
?
?
?
?
=
b=
?
?
A=
*
.
!
*
.
. ! ! .
. ! "
=0.8643154118
y=0.86x+2.62
A=0.8643154118
y=- –
y=13.86
/
$.%(
B=
! .
. !
= 2.629566911
B=2.629566911
r=
?
?
? ?
*& ?
?
=

&#$* #.#$)+ (# .(,) *&#$*#) .,+##'
r=
#$*+#.)+ ,')' (# .(,)(,'. ##*' '()
(# .(,)
= 0.996290

6) cuestionario:
Respecto al problema 2 ¿Qué significado físico tiene la pendiente? y ¿la ordenada al origen?
R.- m=
,
esto nos indica que por cada segundo (tiempo) recorre 0,86cm.
b= 2.62 es a distancia que recorrería en un tiempo mínimo o nulo.
¿Qué observas? Argumenta las ventajas y desventajas de utilizar logaritmos para linealizar.
R.- que podemos visualizar el grado de dependencia entre los datos.
Una ventaja seria que con logaritmos podemos adecuar el diagrama de dispersión a una función que
mejor la represente
Una desventaja seria que se tarda un poco en hacer los cálculos necesarios para llegar a la ecuación
empírica.
Explique cuál es la importancia de aplicar teoría de errores en laboratorio.
R.- porque en los laboratorios las medidas que tomamos en diferentes experimentos no son siempre
correctas o exactas, es decir llamamos error a la diferencia que existe entre la medida y el valor verdadero
de la magnitud, siempre existirá ese error, es lo que podríamos llamar error intrínseco, por inevitable.
¿Cuál es la razón para que en ingeniería debemos basarnos en el mayor error que
encontremos y no en el menor?
R.- porque es más fácil encontrar el mayor error, y en base a eso podemos trabajar más sencillamente.
¿Qué aplicaciones ingenieriles encuentra para la teoría de errores?
R.- porque muchas de las decisiones tomadas en ingeniería, se basan en resultados de medidas
experimentales, por lo tanto es muy importante expresar dicho resultado con claridad y precisión.
Explique a que se denomina eje cartesiano y grafique un eje cartesiano contemplando las
denominaciones de los ejes.
R.- Las coordenadas cartesianas o coordenadas rectangulares (plano cartesiano) son un tipo de
coordenadas ortogonales usadas en espacios euclídeos, para la representación gráfica de una función, en
geometría analítica, o del movimiento o posición en física, caracterizadas porque usa como referencia ejes
ortogonales entre sí que se cortan en un punto origen. Las coordenadas cartesianas se definen así como la
distancia al origen de las proyecciones ortogonales de un punto dado sobre cada uno de los ejes.
Explique paso a paso, el procedimiento de su calculadora científica para calcular una
regresión lineal.
R.- en el modelo Casio fx-570esplus el procedimiento a seguir es el siguiente:

1.
2.
3.
4.
Apretamos la tecla modesetup
Seleccionamos la opción 3 marcando el numero 3
Elegimos el tipo de ecuación que queremos conseguir
Una vez seleccionado nuestro modelo de función nos aparecerá un cuadro para ingresar datos de
la variable x y variable y, para ingresar los dato escribimos un número y apretamos = y así
sucesivamente hasta llegar a nuestro objetivo
5. una vez llenado los pares de coordenadas, apretar la tecla shift+1 y luego apretar la tecla AC 2
veces.
6. volver a apretar las teclas shift+1 y nos aparecerá un menú con 6 opciones de las cuales podremos
deducir los parámetros a,b, coeficiente de correlación, promedio respecto a x o y .. ?xy
,?x…etc. Y muchas otras funciones utilizadas para regresión lineal.
7) Conclusiones:
•
•
Pudimos ajustar las curvas ya sea logarítmica o exponencial o la recta y hallar su ecuación empírica por
el método de mínimos cuadrados
Aprendimos a predecir mediante la extrapolación de datos el comportamiento de variables.
8) análisis de resultados:
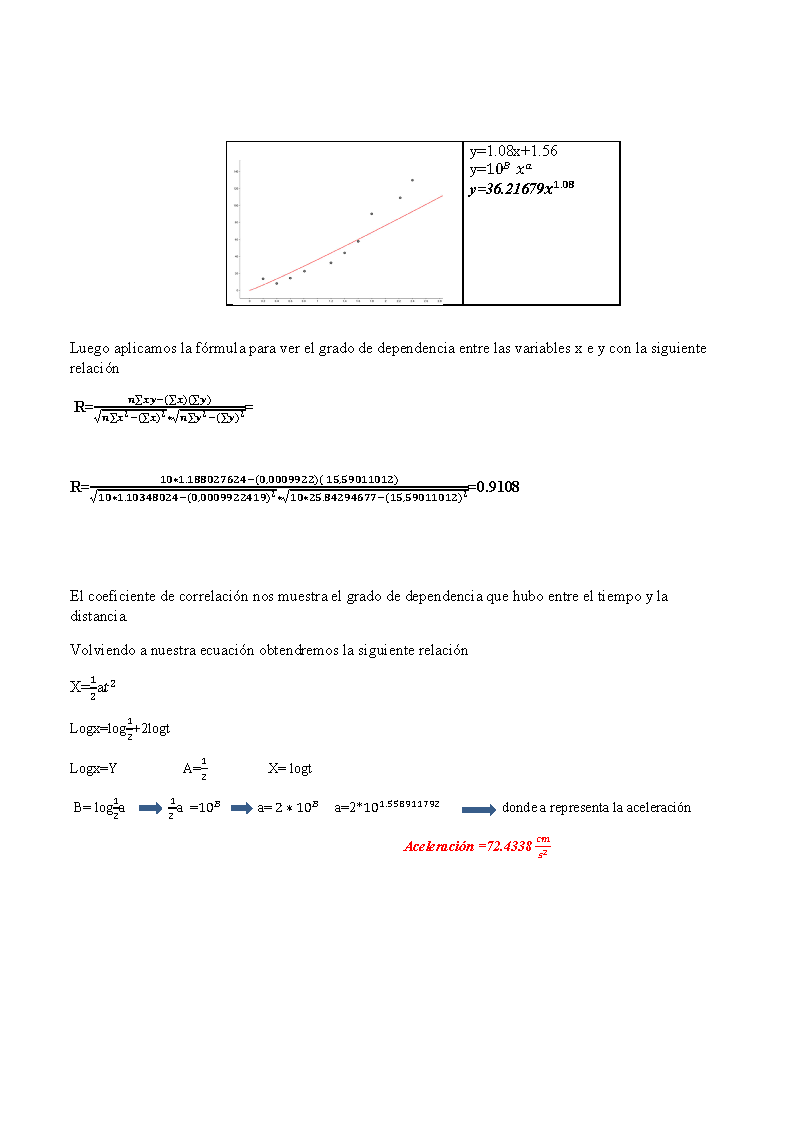
I.)En el experimento 1 pudimos encontrar la ecuación empírica del diagrama de dispersión con los siguientes
datos
Aplicamos log para linealizar de la forma y=bx^a y llevarla a la forma Y=Ax+B
Calculamos parámetros a y b de la ecuación Y=Ax+B con las siguientes relaciones:
A=
?
?
(? )(? )
(? )
=
B=
?
–
?
&#$*#.#$,)%$ )
a =10
y=1.08x+1.56
y=10
y=36.21679 #.$%
Luego aplicamos la fórmula para ver el grado de dependencia entre las variables x e y con la siguiente
relación
R=
& ?
?
?
? ?
*& ?
?
=
R=
#$*#.#%%$ '( ) $,$$$** #+,+*$##$#
$,$$$** )#* *&#$* +.%) *)(''
#+,+*$##$#
=0.9108
El coeficiente de correlación nos muestra el grado de dependencia que hubo entre el tiempo y la
distancia.
Volviendo a nuestra ecuación obtendremos la siguiente relación
X= a
Logx=log +2logt
Logx=Y
A=
X= logt
B= log a
a= 2 * 10
a=2*10
.
donde a representa la aceleración
Aceleración =72.4338
1
2

II.) En el experimento 2 pudimos encontrar la ecuación empírica del diagrama de dispersión con los
siguientes datos usando logaritmo neperiano
Aplicamos ln para linealizar de la forma y=b-
/
y llevarla a la forma Y=Ax+B
Calculamos parámetros a y b de la ecuación Y=Ax+B con las siguientes relaciones:
A=
?
?
?
?
?
=
B=
?
?
y=0.86x+2.62
y=- – /
y=13.86 $.%(
Luego aplicamos la fórmula para ver el grado de dependencia entre las variables x e y con la siguiente relación
r=
& ?
?
?
? ?
*& ?
?
=
#$*+#.)+ ,')' # .(, ,'. ##*' '(
r=
&#$* #.#$)+ # .(, *&#$*#) .,+##' # .(,
= 0.996290
El coeficiente de correlación nos muestra el grado de dependencia que hubo entre el tiempo y la distancia
Volviendo a nuestra ecuación del ejercicio obtendremos la siguiente relación
X= a

Lnx=ln 3+2lnt
B=ln 3
b=-
a=2-
donde a es la aceleración
a=2-
.
aceleracion=27.7355
1
2
9) Recomendaciones:
la práctica salió todo bien, pero sería mejor que el docente explique más a fondo el tema para así poder
comprender mejor lo que hacemos.
10) Bibliografía:
estadística para ingenierías y científicos – William Naidi
estadística – Schaum 4ta edición
probabilidad y estadística para ingenierías y ciencias – Jay L. Devore – séptima edición
probabilidad y estadística – Walpole Myers Myers Ye – octava edición
Materias básicas- guía práctica de laboratorio