Probabilidad
total

entonces, la probabilidad del evento B, llamada
probabilidad total, se calcula empleando la siguiente
fórmula:

Teorema de
Bayes
El teorema de Bayes se utiliza para revisar
probabilidades previamente calculadas cuando se posee nueva
información. Desarrollado por el reverendo Thomas Bayes en
el siglo XVII, el teorema de Bayes es una extensión de lo
que ha aprendido hasta ahora acerca de la probabilidad
condicional.
Comúnmente se inicia un análisis de
probabilidades con una asignación inicial, probabilidad a
priori. Cuando se tiene alguna información adicional se
procede a calcular las probabilidades revisadas o a posteriori.
El teorema de Bayes permite calcular las probabilidades a
posteriori y es:

Ejemplos
ilustrativos
1) Una compañía de transporte
público tiene tres líneas en una ciudad, de forma
que el 45% de los autobuses cubre el servicio de la línea
1, el 25% cubre la línea 2 y el 30% cubre el servicio de
la línea 3. Se sabe que la probabilidad de que,
diariamente, un autobús se averíe es del 2%, 3% y
1% respectivamente, para cada línea.
a) Calcular la probabilidad de que, en un día, un
autobús sufra una avería
b) Calcular la probabilidad de que, en un día, un
autobús no sufra una avería
c) ¿De qué línea de transporte es
más probable que un autobús sufra una
avería?
Solución:

a) Calcular la probabilidad de que, en un día, un
autobús sufra una avería
Empleando la fórmula de probabilidad total se
obtiene:
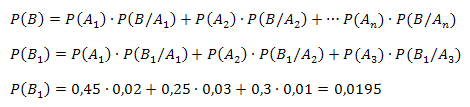
b) Calcular la probabilidad de que, en un día, un
autobús no sufra una avería
Empleando la fórmula de probabilidad total se
obtiene:

c) ¿De qué línea de transporte es
más probable que un autobús sufra una
avería?
Se debe calcular las tres probabilidades aposteriori
empleando el Teorema de Bayes

La probabilidad de que sea de la línea 1,
sabiendo que sufre una avería es:

La probabilidad de que sea de la línea 2,
sabiendo que sufre una avería es:

La probabilidad de que sea de la línea 3,
sabiendo que sufre una avería es:

Entonces, sabiendo que el autobús sufre una
avería, lo más probable es que sea de la
línea 1, ya que esta probabilidad

, es la mayor.
Los cálculos en Excel se muestran en la siguiente
figura:

2) Una empresa dedicada a la comercialización de
televisores está considerando comercializar un nuevo
televisor. En el pasado el 90% de los televisores que
comercializó tuvieron éxito y el 10% no fueron
exitosos. Se sabe que la probabilidad que habría recibido
un reporte favorable de investigación fue del 85% y 35%,
respectivamente.

Solución:
a) Escribir la simbología del problema
A1 = Televisores exitosos
A2 = Televisores no exitosos
B1 = Reporte favorable de
investigación
B2 = Reporte desfavorable de
investigación
La solución del problema en Excel se muestra en
la siguiente figura:

3) La probabilidad de que una persona tenga una
determinada enfermedad es de 0,02. Existen pruebas de
diagnóstico médico disponibles para determinar si
una persona tiene realmente la enfermedad. Si la enfermedad
realmente está presente, la probabilidad de que la prueba
de diagnóstico indique la presencia de la enfermedad es de
0,95.

Solución:
La solución del problema en Excel se muestra en
la siguiente figura:

4) Una fábrica de sacos tiene 3 máquinas
independientes que producen el mismo tipo de sacos. La
máquina 1 produce el 15% de los sacos con un 1% de sacos
defectuosos. La máquina 2 produce el 45% de los sacos con
un 3% de sacos defectuosos. La máquina 3 produce el 40% de
los sacos con un 2% de sacos defectuosos.

Solución:
La solución del problema en Excel se muestra en
la siguiente figura:

5) El primer año de bachillerato de un colegio
está integrado por 35 estudiantes en la especialidad de
físico matemático, 47 en químico
biólogo, 40 en sociales y 38 en bachillerato general. Se
sabe que la probabilidad de que un estudiante pierda el
año es del 5% 4%, 3% y 4%, respectivamente. ¿De
qué especialidad es más probable que sea el
estudiante, si se sabe que un estudiante ha perdido el
año?
Químico biólogo con
0,296
Solución:
La solución del problema en Excel se muestra en
la siguiente figura:

Autor:
Mario Orlando Suárez
Ibujes