Compendio histórico de los problemas matematicos sin solución

"La principal razón de existir del
matemático es

Resolver problemas, y por lo tanto en lo
que realmente

Consisten las matemáticas es en
problemas y soluciones."

Paul R. Almos [14]

Introducción

La palabra problema proviene del griego
lanzar adelante"

Un problema es un obstáculo arrojado
ante la inteligencia para ser superado, Una dificultad que exige
ser resuelta, una cuestión que reclama ser
aclarada.

Todos vivimos resolviendo problemas: desde el más
básico de asegurar la Cotidiana subsistencia, común
a todos los seres vivos, hasta los más complejos
desafíos planteados por la ciencia y la tecnología.
La importancia de la actividad de resolución de problemas
es evidente; en definitiva, todo el progreso científico y
tecnológico, el bienestar y hasta la supervivencia de la
especie humana dependen de esta habilidad. No es de
extrañar por lo tanto que la misma se haya convertido en
un nuevo objeto de estudio, atrayendo por igual la
atención de psicólogos, ingenieros,
matemáticos, especialistas en inteligencia artificial y
científicos de todas las disciplinas.

"Resolver un problema es hacer un descubrimiento. Un
gran problema significa un gran descubrimiento, pero hay una
partícula de descubrimiento en la solución de
cualquier problema. El suyo puede ser modesto, pero si pone a
prueba la curiosidad que induce a poner en juego las facultades
inventivas, y si lo resuelve por medios propios, puede
experimentar la tensión y el encanto del descubrimiento y
el goce del triunfo.

Evidentemente la resolución de problemas
está estrechamente relacionada con la creatividad, que
algunos definen precisamente como la habilidad para generar
nuevas ideas y solucionar todo tipo de problemas y
desafíos.

El pensamiento creativo se ha dividido en divergente y
convergente. El primero consiste en la habilidad para pensar de
manera original y elaborar nuevas ideas, mientras que el segundo
se relaciona con la capacidad crítica y lógica para
evaluar alternativas y seleccionar la más
apropiada.

CAPITULO I

Conceptos
básicos

• LOS PROBLEMAS EN LA
  MATEMÁTICA.

La matemática como ciencia surge a partir de la
filosofía, ciencia que en aquella época
incluía a las demás, es decir era la ciencia de
todas las ciencias. En sus inicios los conocimientos
matemáticos estaban relacionados únicamente con las
necesidades inmediatas de la vida cotidiana como la de contar,
numerar, distribuir, medir áreas de parcelas de tierra,
volumen de vasijas, etc.; en esta etapa se comienza a implantar
los fundamentos de la matemática como ciencia; por ejemplo
en la Grecia antigua se llegaron a sistematizar los
métodos de solución de problemas de la
aritmética elemental apareciendo la disciplina
Aritmética.

El desarrollo histórico de las matemáticas
es estimulado por problemas de las ciencias naturales, así
la aritmética y el álgebra surgieron como respuesta
a necesidades humanas en materia de contabilidad y
administración; la geometría y trigonometría
se desarrollan a partir de problemas de medidas, agrimensura y
astronomía, además se desarrollaron otras ramas que
se originaron no sólo como consecuencias de problemas de
las ciencias naturales, sino también de las sociales y de
distintos campos del esfuerzo humano

La categoría problema ha estado presente a lo
largo del desarrollo histórico de las matemáticas,
tanto por la presencia de problemas de la vida social, como de
las ciencias naturales y de la propia matemática que han
propiciado su enriquecimiento teórico. El surgimiento de
la Matemática está muy relacionado con el
planteamiento y solución de problemas. Desde la
antigüedad el hombre se ha enfrentado a esta actividad y tan
importante ha sido el hecho de encontrarles respuestas como de
formularlos correctamente para el desarrollo ulterior de la
ciencia.

En relación con el concepto de problema
matemático, son muchas las definiciones que se han
ofrecido, las mismas en su esencia no resultan contradictorias,
pero revelan los puntos de vista de sus autores al
abordarlas.

• Algunas definiciones de problema:

• Un problema tiene ese carácter, ante todo,
  porque nos presenta puntos desconocidos en los que es
  necesario poner lo que falta", (Rubinstein, S.L.1966;
  p.24).

• Es una forma subjetiva de expresar la necesidad de
  desarrollar el conocimiento científico" (Majmutov, M.
  1983; p.58).

• Un problema representará una verdadera
  situación nueva" (Dávidson, L. 1987;
  p.1).

• Un problema es toda tarea que requiere de un
  esfuerzo por parte del alumno para ser resuelto" (Antibi,
  A.1990; p. 23).

• Contradicción entre una situación
  actual del objeto y una situación deseable. Revela un
  segmento de la realidad donde el conocimiento es insuficiente
  o parcial, o en el cual prevalecen modos de actuación
  insatisfactorios, expresando al mismo tiempo, que la
  respuesta o solución no está contenida en la
  región de lo conocido. Ello conduce al despliegue de
  una actividad para resolver la contradicción y llegar
  a la situación deseable"(Centro de Estudios
  Educacionales. 1999; p.5).

• Estas definiciones anteriores expresan una
  concepción general del concepto
  problema. Proposición que se formula para, a
  partir de ciertos datos conocidos, hallar el valor
  numérico o resultado correspondiente a la
  cuestión o pregunta planteada" (De Galiano, T. 1991;
  p. 835).

• Se refiere a aquellas cosas que son verdaderamente
  problemitas para las personas que trabajan en ellas, se asume
  que estas personas no tienen a mano un procedimiento de
  rutina para la solución" (Schoenfield, A. 1993;
  p.121).

• Se denomina problema a toda situación en la
  que hay un planteamiento inicial y una exigencia que obliga a
  transformarlo. La vía para pasar de la
  situación o planteamiento inicial a la nueva
  situación exigida tiene que ser desconocida y la
  persona debe querer hacer la transformación"
  (Campistrous, L y Rizo, C. 1996; p. IX y X).

• Un ejercicio es un problema si y sólo si la
  vía de solución es desconocida por la persona"
  (Llivina, M. 1999; p. 48).

En las definiciones anteriores puede
apreciarse que en algunos casos se refieren a ejercicios o tareas
en su sentido amplio, que deben cumplir determinadas exigencias y
en otros casos, se conciben como la exposición en el
lenguaje común de determinados hechos, fenómenos u
objetos, también bajo determinadas exigencias. En general,
se concibe la existencia de una contradicción entre lo que
se desea hacer y lo conocido para ello.

• Pero considera válido
  añadir un elemento no explícito en ella y que
  refieren Campistrous, L. y Rizo, C. (1996), es
  decir:

La persona debe querer resolver el problema
(motivación).Los problemas están caracterizados por
tener una situación inicial conocida (datos) y una
situación final desconocida (incógnita), siendo su
vía de solución desconocida y la misma se obtiene a
través de procedimientos
heurísticos. 

Los elementos anteriores caracterizan la
estructura externa de los problemas.  Cuando se habla de la
estructura de un problema matemático con texto, se asumen
las partes o los elementos estructurales que conforman el
problema  En este caso, se considera la siguiente estructura
externa:

Datos: Magnitudes, números, relaciones
matemáticas explícitas entre los números,
como: el duplo de; la mitad parte de; aumentado en; el cuadrado
de; entre otras.

Condiciones: Relaciones matemáticas no
explícitas entre lo dado y lo buscado, vinculadas con la
estrategia de solución, como: las derivadas de los
significados prácticos de las operaciones de
cálculo, propiedades, teoremas, recursos
matemáticos a utilizar, no declarados en el
problema.

Pregunta: La incógnita, lo que hay que
averiguar.

En un contexto general podemos decir que un problema es
una determinada cuestión o asunto que requiere de una
solución. A nivel social, se trata de algún asunto
particular que, en el momento en que se solucione,
aportará beneficios a la sociedad (por ejemplo, lograr
disminuir la tasa de pobreza de un país).

La filosofía establece que un problema es algo
que perturba la paz y la armonía de quien o quienes lo
tienen. Para la religión, un problema puede ser una
contradicción interna entre dos dogmas
(¿cómo un Dios omnibenevolente y todopoderoso
permite la existencia del sufrimiento?).

Para las ciencias matemáticas, un problema es una
pregunta sobre objetos y estructuras que requiere una
explicación y demostración. En otras palabras, un
problema matemático consiste la búsqueda de una
determinada entidad matemática que permita satisfacer las
condiciones del problema. Los problemas matemáticos pueden
ser de cálculo, geométricos, algebraicos y no
algorítmicos.

Por otra parte, se denomina problema didáctico al
ejercicio de raciocinio que puede resolverse con la
utilización de las matemáticas y de la
lógica. De esta forma, un problema de este tipo debe
contar con tres elementos básicos: los datos necesarios
para resolverlo (siempre explícitos), el método o
relación entre los datos (que es lo que el estudiante debe
averiguar) y el resultado buscado (al que se llega tras seguir
ciertas reglas de razonamiento y supuestos que surgen de los
datos).

Los problemas didácticos suelen ser
matemáticos y se utilizan en todos los niveles educativos
para enseñar a asociar situaciones del mundo real con el
lenguaje abstracto de las matemáticas y a pensar con
lógica.

Para resolver cualquier tipo de problema
didáctico-matemático, hay que seguir tres pasos
básicos: comprender lo que se está preguntando,
abstraer el problema (encontrar una expresión
matemática que permita representar el problema y
resolverlo) y entender que quiere decir el resultado al que se ha
llegado.

Entre los campos que son un producto específico
del siglo XX mencionaremos simplemente cuatro ejemplos que por Lo
tanto no pretenden ser, ni mucho menos exhaustivos de los avances
de la Matemática. En primer lugar la Topología, es
decir el estudio de las formas de las variedades, introducido por
Poincaré (foto) a comienzos de siglo y que ha
experimentado un desarrollo espectacular a lo largo del siglo de
la mano de nombres como Serre, Milnor, Smale o
Thurston.

En segundo lugar, el manejo del azar, La probabilidad y
el análisis estocástico son otra de las grandes
creaciones del siglo pasado. Si bien es cierto que ya
existían estudios sobre la probabilidad desde la
época de Fermat, Pascal e incluso antes, pero es en el
siglo XX cuando a partir de la axiomatización del modelo
probabilístico por Kolmogorov, y más tarde de la
herramienta fundamental del análisis estocástico:
la integral estocástica, por Kiyositó cuando la
disciplina toma vuelo hasta construirse en una de Las
áreas más activas en la actualidad. Piénsese
que prácticamente todos los fenómenos encierran una
componente aleatoria, por lo que el análisis
estocástico es imprescindible en ellos.

En tercer lugar el estudio de los sistemas
dinámicos y en particular de tos fenómenos no
lineales ha sido también una de las áreas de
desarrollo espectacular en el siglo XX: en las ecuaciones que
regulan la evolución un proceso concreto se observa que a
menudo aparecen términos no lineales. Un ejemplo
importantísimo son las ecuaciones de Navier-Stokes que
regulan la dinámica de fluidos. La existencia de estos
términos no lineales conduce a comportamientos
caóticos que hoy sabemos que aparecen con muchísima
frecuencia, por lo que el estudio de la estabilidad de las
soluciones de un sistema dinámico es muy importante. Uno
de los resultados más llamativos del siglo es el llamado
teorema KAM (KoLmogorov, Arnold y Moser) de los años 60
relativo a la estabilidad de las órbitas del problema de
Los n cuerpos (por ejemplo el sistema solar) y que nos aporta
cierta tranquilidad acerca de que nuestro planeta
continuará en una órbita parecida (pero nunca
igual) a la que ha venido teniendo desde su origen.

Y por último no podemos olvidar los estudios
sobre lógica, computabilidad y complejidad que impulsados
por nombres como Turing, Gódel, Von Neumann, etc. han
conducido a la creación de la computadora, el invento del
siglo XX que está transformando radicalmente nuestra
sociedad.

• LA FORMULACIÓN DE
  PROBLEMAS 

La formulación de problemas se ha visto como un
complemento de la solución de problemas, la
profundización en la misma, las orientaciones a seguir,
así como las potencialidades que ésta tiene no han
sido objeto de un estudio sistemático, por lo que la
bibliografía o documentos de consulta para ella resultan
insuficientes. Los trabajos relacionados con la
formulación de problemas, Labarrere (1980; 1983),
Campistrous y Rizo (1996), González, D (2000), e Inerarity
(2003) están dirigidos a la enseñanza primaria, por
ser en ésta donde debe formarse dicha
habilidad.

Es un error pensar que las tareas que
implican la utilización de algoritmos conocidos o para las
que existen fórmulas constituyen verdaderos problemas. La
clasificación, seriación y ordenación de
objetos, la utilización de distintos tipos de medidas, el
análisis de regularidades entre determinados hechos, etc.,
pueden constituir problemas con objetivos tan diversos como
traducir las experiencias cotidianas a un lenguaje
común.

"Es más importante descubrir
problemas que resolverlos; una psiquis que problematiza su
realidad se anticipa a las futuras experiencias, y por lo tanto
puede dar mejores respuestas a los problemas de la vida cotidiana
que se presentan".Estos procesos se complementan, pues
contribuyen a:

* Conocer el concepto de
problema

* Reconocer los componentes de un
problema

* Plantear y buscar relaciones entre los
componentes

* Desarrollar habilidades en la
traducción del lenguaje común al algebraico y
viceversa

* Reconocer modelos matemáticos para
solucionar tipos de problemas

* La determinación de problemas auxiliares, etc.
No obstante, aunque la formulación y solución de
problemas se complementan, son procesos que tienen sus
respectivas características y complejidades que los
constituyen etapas independientes de la actividad cognoscitiva.
Una exigencia del programa de Matemática que actualmente
se aplica en las secundarias básicas es que los alumnos
aprendan a resolver y también a formular problemas, por lo
que ésta última merece en lo adelante nuestra
atención, por lo que se evidencia la necesidad de
fortalecer la superación de los profesores para dirigir el
proceso de formulación de problemas que les permita
desarrollar las acciones intelectuales necesarias para sus
alumnos.

• MATEMATICA DEL SIGLO XX

Aunque ya nos encontramos en el siglo XXI es bastante
temerario hacer un balance de Hitos Matemáticos del siglo
pasado. En primer lugar porque la perspectiva es aún
escasa y, en segundo lugar y más importante, porque las
propias características de la Matemática del siglo
XX, marcadas por un desarrollo sin precedentes y una amplitud de
temas extraordinaria, hace que sea muy difícil por no
decir imposible la catalogación de Los hitos fundamentales
de la ciencia matemática. Esto se debe a diversas
causas.

En primer lugar, porque la producción
matemática del siglo XX ha superado (en cuanto a
extensión y posiblemente en cuanto a calidad) a la
producción en toda la historia anterior. Por citar algunos
datos: en La década de Los 90 se han publicado una media
de más de 50.000 trabajos anuales de investigación
en Matemática en las revistas especializadas del todo el
mundo.

Junto a la cantidad de producción, la segunda
causa es, sin duda, la diversidad de campos que ella abarca: a lo
largo del siglo XX han surgido y se han desarrollado áreas
completamente nuevas, y los resultados matemáticos han
impregnado prácticamente todas las parcelas de nuestra
vida cotidiana. Como resultado, el desarrollo tecnológico
y científico del siglo XX no ha tenido parangón en
la historia de la humanidad. Conviene no perder de vista esta
perspectiva: la Matemática es la base, los rieles sobre
los que caminan las ciencias y la tecnología; sin un
desarrollo matemático no puede haber un desarrollo
científico parejo y la historia está llena de
ejemplos que muestran como sólo cuando la maquinaria
matemática ha desarrollado los conceptos y técnicas
adecuadas se han podido dar nuevas teorías y grandes pasos
científicos. Citemos tres ejemplos típicos del
siglo XX: la Teoría de La Relatividad de Einstein,
imposible sin el desarrollo de la Geometría diferencial
moderna, los estudios sobre compatibilidad que de la mano de Von
Neumann condujeron a la creación de las computadoras, y
los trabajos de Shannon sobre la Teoría Matemática
de la Comunicación de los años 1948 y 50 que
sentaron las bases de la Teoría de Códigos y por
consiguiente de la moderna transmisión de
datos.

CAPITULO II

Generalidades

PROBLEMAS CON Y SIN
SOLUCIÓN

El conocimiento matemático del mundo moderno
está avanzando más rápido que nunca.
Teorías que eran completamente distintas se han reunido
para formar teorías más completas y abstractas.
Aunque la mayoría de los problemas más importantes
han sido resueltos, siguen sin solución. Al mismo tiempo
siguen apareciendo nuevos y estimulantes problemas. Parece que
incluso las matemáticas más abstractas están
encontrando aplicación.

2.1 PROBLEMAS CON ÚNICA
SOLUCIÓN:

2.2 PROBLEMAS CON VARIAS SOLUCIONES O
INFINITAS

2.3 PROBLEMAS SIN SOLUCION, ABIERTOS O NO
RESUELTO

En ciencia y matemáticas, un problema no resuelto
o problema abierto, es un problema que puede ser formulado con
mucha precisión, y todavía no ha sido resuelto (ya
que no hay solución conocida para él). Ejemplos
notables de grandes problemas matemáticos que han sido
resueltos y cerrados por los investigadores en

Existen importantes problemas no resueltos en muchos
campos, tales como la ciencia computacional teórica, la
física y las matemáticas. Uno de los problemas
abiertos más importantes en bioquímica es
cómo predecir la estructura de una proteína desde
su secuencia, este es el llamado problema de la predicción
de la estructura de las proteínas.

Es común en las escuelas de postgrado
señalar los problemas no resueltos a los estudiantes. Los
estudiantes de posgrado, así como los miembros de la
facultad a menudo se involucran en la investigación para
resolver dichos problemas.

La antigua Grecia fue la cuna de la geometría que
se conoce en nuestros días. Célebres personajes
enunciaron los teoremas que usamos en la actualidad como Tales de
Mileto, que fue quien introdujo los conocimientos sobre
geometría de los egipcios en Grecia y quien enunció
la conocida teoría de los triángulos semejantes.
Otras dos escuelas que tuvieron un papel central en la
geometría griega fueron la de Pitágoras y la de
Euclides.

El primero fue quien enunció el famoso teorema
que lleva su nombre sobre la relación de los catetos y la
hipotenusa de un triángulo rectángulo. Euclides,
por su parte fue quien con sus postulados sentó casi
definitivamente las bases de toda la geometría griega,
excepto por otros personajes posteriores a su muerte.
Arquímedes y Apolonio son los dos más destacables
de ese período con sus trabajos en cónicas y
tangencias respectivamente.

Sin embargo, a pesar del enorme paso que se produjo en
el mundo de la geometría en esa época, hubo tres
famosos problemas que los matemáticos griegos de entonces
no supieron resolver.

• PROBLEMAS CLASICOS DE LA
  ANTIGUEDAD

• LA CUADRATURA DEL CÍRCULO:

Se denomina cuadratura del círculo al problema
matemático, irresoluble de geometría, consistente
en hallar -con sólo regla y compás- un cuadrado que
posea un área que sea igual a la de un círculo
dado, solo se puede calcular por el método de repeticiones
sucesivas.

La resolución de este problema trató de
abordarse repetidas veces, sin éxito, desde la
antigüedad clásica hasta el siglo XIX. Hablando en
sentido figurado, se dice de algo que es la "cuadratura del
círculo" cuando representa un problema muy difícil
o imposible de resolver.

La posibilidad de cuadrar superficies limitadas por
curvas (superficies curvilíneas) y, en especial, la
cuadratura del círculo, no habría parecido tan
plausible a los griegos de no haber sido por el hecho de que
Hipócrates de Quíos demostró que ciertas
figuras curvilíneas construidas a propósito por
él, llamadas lúnulas, podían cuadrarse. La
resolución de la cuadratura de las lúnulas de
Hipócrates creó una falsa expectativa entre los
matemáticos de la antigüedad, llevándoles a
pensar que podría cuadrarse el círculo.

En el siglo XX Chebotariov y Dorodnov probaron que, en
general, las lúnulas no pueden cuadrarse excepto los tres
tipos de lúnulas propuestos por Hipócrates y dos
tipos más aportados por Leonhard Euler en el siglo XVIII.
De esta forma quedó de manifiesto que la cuadratura de la
lúnula no era otra cosa que una solución
excepcional de un problema irresoluble, cosa que confundió
a los matemáticos durante siglos creyendo que las
lúnulas podrían acercarlos a la cuadratura del
círculo.

En 1882, el matemático alemán Ferdinand
Lindemann probó que p es un número trascendente, lo
que implica que es imposible cuadrar el círculo usando
regla y compás, resolviendo completamente el problema. Las
pruebas usuales usan álgebra (teoría de Galois por
ejemplo) y variable compleja.

• LA DUPLICACIÓN DEL CUBO

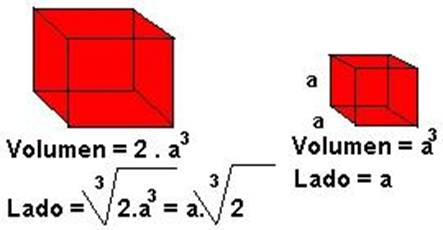
Se denomina duplicación del cubo al problema de
hallar, mediante el uso de regla y compás, el lado de un
cubo tal que su volumen sea el doble del volumen de otro cubo de
lado dado. Actualmente los instrumentos del álgebra son
capaces de resolver este problema de forma trivial, pero la
restricción de regla y compás era muy
fuerte

• HISTORIA DEL PROBLEMA DE DUPLICACION DEL
  CUBO

En el año 429 a. C., Pericles, gobernador de
Atenas por esa época, muere víctima de la peste que
atacaba muy severamente la ciudad. A raíz de este suceso
algunos de los habitantes deciden ir a la ciudad de Delfos para
hacer consultas al Oráculo de Apolo y saber cómo
poder detener la epidemia. La respuesta a la consulta del
Oráculo es que deben elaborar un nuevo altar en forma de
cubo cuyo volumen duplique el del altar que ya existe. Lo
intentaron, es muy seguro, pero también fue igualmente
seguro que no lograron evitar el desastre por este medio. La
pandemia se disipó con el tiempo, pero el problema
matemático planteado permaneció.

De esta forma se inicia lo que se denominará uno
de los problemas clásicos de las matemáticas: la
duplicación del cubo.

Los primeros intentos por resolverlo:

El primero en abordar el problema sin éxito fue
el griego Hipócrates de Quíos. Basándose en
el mismo planteamiento lo intentaron otros matemáticos
posteriores, tales como Arquites de Tarento, Menecmo y
Eratóstenes de Cirene, pero todos ellos presentan
soluciones aproximadas, en ninguna de las cuales puede resolverse
el problema en forma exacta.

La solución: Desgraciadamente, lo único
que se pudo comprobar al cabo del tiempo y ya en 1837 fue que el
problema no tiene solución, hecho demostrado gracias a los
trabajos del geómetra francés Pierre Wantzel.
Pierre Laurent Wantzel este matemático francés nace
en París, 5 de junio de 1814 – y fallece en París
el 21 de mayo de 1848) este señor demostró que
varios problemas geométricos antiguos son imposibles de
resolver usando únicamente regla y compás. La
solución a estos problemas había sido buscada
durante miles de años, en particular por los antiguos
griegos. Wantzel publicó en el año 1837 en una
revista de matemáticas francesa la primera prueba
completamente rigurosa de la imposibilidad de trisecar un
ángulo con la sola ayuda de una regla y un compás.
Wantzel demostró igualmente la imposibilidad de resolver
la duplicación del cubo; y la construcción de un
polígono regular cuyo número de lados no es
producto de una potencia de dos o distinto a cualquier
Número de Fermat.

• LA TRISECCION DEL ÁNGULO:

La trisección del ángulo es, junto a la
cuadratura del círculo y la duplicación del cubo,
uno de los problemas clásicos de las matemáticas de
la antigua Grecia. Se ha demostrado que estos tres problemas, en
general, son imposibles de resolver usando únicamente
regla y compás, aunque son muy recurridas las
aproximaciones.

La trisección del ángulo fue el tercero de
los problemas clásicos de la antigüedad griega. Se
pretendía trisecar un ángulo, o dicho de otra
forma, dividirlo en tres partes perfectamente iguales usando
sólo una regla (no graduada) y un compás. Esto, en
general, no es posible. Un ejemplo sencillo en donde sí es
posible es dividir el ángulo de 90° en 30°. La
división de un ángulo cualquiera en su tercera
parte, puede lograrse introduciendo curvas auxiliares que
permiten su construcción.

El problema de la trisección del ángulo
-aunque se ignora su origen- no sería aventurado suponer
que se lo plantearon los geómetras cuando supieron
bisecarlo por el método que hemos aprendido en el
Bachillerato, durante cuyos estudios también nos han dicho
que el problema de la trisección es posible en algunos
casos particulares: posible -se entiende- con regla y
compás.

Para la solución general los griegos utilizaron
la curva construida por Hippias de Elea llamada después
cudratriz porque también servía para cuadrar el
círculo. La cuadratiz (fig. 19) es la curva que pasa por
los puntos de intersección de las diversas posiciones del
lado AB del cuadrado ABCD girando con movimiento uniforme
alrededor de A hasta ocupar la posición AD y el lado BC
trasladándose paralelamente a sí mismo y
también con movimiento uniforme hasta llegar
también a AD.

Hippias imaginó un aparato para describir
mecánicamente la curva, de cuya generación se
deduce que trazan una recta cualquiera AB, la razón de
cuadrante BED al arco BE es la misma que la del segmento BA al
GH, de modo que para trisecar el ángulo EAD basta
determinar JI = 1/3GH y el ángulo JAD es la tercera parte
del EAD.

Los problemas de duplicar el cubo y trisecar el
ángulo, son problemas irracionales, es decir problemas
cuyas soluciones son irracionales, y como dependen de
 ecuaciones de tercer grado no se pueden resolver con
 a regla y el compás  por exigir construcciones
en el espacio. La cuadratura del círculo es de otra
naturaleza, pues depende del número PI que no puede ser
solución de ninguna ecuación de coeficientes
enteros, según demostró Lindemann el año
1882, y, por tanto, dicha cuadratura también  es
imposible con regla y compás.  A pesar de que desde
el año 1775 la Academia de Ciencias de París
tomó el acuerdo -adoptado después por otras- de
rechazar las pretendidas soluciones de estos tres problemas,
siguen lloviendo sobre las corporaciones, científicas
multitud de comunicaciones acerca de los mismos, que,
naturalmente, van a parar al cesto de papeles sin ser
leídas, y esto -que ya está divulgado hasta la
saciedad de libros y revistas- no ha bastado, ni basta, ni
bastará para curar la enfermedad que padecen los
duplicadores, trisectores y cuadradores, a los que hay que
añadir los "demostradores» del Postulado de
Euclides, empeñados en no emplear más armas que las
de los griegos antiguos porque ignoran la existencia de las
bombas atómicas de la Matemática actual que han
demostrado la insuficiencia de los primitivos artefactos
bélicos. Ni qué decir tiene que la ignorancia de
los duplicadores, trisectores, cuadradores y postuladores, va
unida a una insigne pedantería que les inspira un
olímpico desdén por quienes les aconsejan
honestamente que se enteren de los trabajos hechos por sus
predecesores para soslayar el peligro de descubrir
Mediterráneos, porque todos ellos excepción- se
creen genios desconocidos, y desde 1uego superiores al medio
matemático de su época, y los más enterados
se consideran en el caso de un Ruffini, que no con siguió
que el Instituto de Francia  examinara su
demostración de la imposibilidad de resolver por radicales
las ecuaciones algebraicas de grado superior al cuarto, o de un
Grauss, que no quiso publicar sus investigaciones sobre las
Geometrías no-euclídeas por temor al "clamoreo de
los beocios".

• HISTORIA DE LAS ECUACIONES

La primera fase, que comprende el periodo de 1700 a. de
C. a 1700 d. de C., se caracterizó por la invención
gradual de símbolos y la resolución de ecuaciones.
Dentro de esta fase encontramos un álgebra desarrollada
por los griegos (300 a. de C.), llamada álgebra
geométrica, rica en métodos geométricos para
resolver ecuaciones algebraicas.

La introducción de la notación
simbólica asociada a Viète (1540-1603), marca el
inicio de una nueva etapa en la cual Descartes (1596-1650)
contribuye de forma importante al desarrollo de dicha
notación. En este momento, el álgebra se convierte
en la ciencia de los cálculos simbólicos y de las
ecuaciones. Posteriormente, Euler (1707-1783) la define como la
teoría de los "cálculos con cantidades de distintas
clases" (cálculos con números racionales enteros,
fracciones ordinarias, raíces cuadradas y cúbicas,
progresiones y todo tipo de ecuaciones).

Para llegar al actual proceso de resolución de la
ecuación   ax + b = c   han pasado más de
3.000 años.

Los egipcios nos dejaron en sus papiros (sobre todo en
el de Rhid -1.650 a. de C- y el de Moscú -1.850 a, de C.-)
multitud de problemas matemáticos resueltos. La
mayoría de ellos son de tipo aritmético y
respondían a situaciones concretas de la vida diaria; sin
embargo, encontramos algunos que podemos clasificar como
algebraicos, pues no se refiere a ningún objeto concreto.
En éstos, de una forma retórica, obtenían
una solución realizando operaciones con los datos de forma
análoga a como hoy resolvemos dichas
ecuaciones.

Las ecuaciones más utilizadas por los egipcios
eran de la forma:

x + ax = b

x + ax + bx = 0

Donde a, b y c eran números conocidos y   x
  la incógnita que ellos denominaban aha o
montón.

Una ecuación lineal que aparece en el papiro de
Rhid responde al problema siguiente:

"Un montón y un séptimo del
mismo es igual a 24".

En notación moderna, la
ecuación sería:    x + 1 / 7 x =
24

La solución la obtenía por un
método que hoy conocemos con el nombre de "método
de la falsa posición" o "regula falsi". Consiste en tomar
un valor concreto para la incógnita, probamos con
él y si se verifica la igualdad ya tenemos la
solución, si no, mediante cálculos obtendremos la
solución exacta.

Supongamos que fuera   7   la solución,
al sustituir en la x nos daría:   7 + 1/7
· 7 = 8, y como nuestra solución es 24, es decir,
8·3, la solución es 21 = 3 · 7, ya que 3
· (7 + 1/7 – 7) = 24.

Generalmente, el cálculo de la solución
correcta no era tan fácil como en este caso e implicaba
numerosas operaciones con fracciones unitarias (fracciones con
numerador la unidad), cuyo uso dominaban los egipcios. En cuanto
el simbolismo, solamente en algunas ocasiones utilizaban el
dibujo de un par de piernas andando en dirección de la
escritura o invertidas, para representar la suma y resta,
respectivamente. Los babilonios (el mayor número de
documentos corresponde al periodo 600 a. de C. a 300 d. de C.)
casi no le prestaron atención a las ecuaciones lineales,
quizás por considerarlas demasiado elementales, y
trabajaron más los sistemas de ecuaciones lineales y las
ecuaciones de segundo grado.

Entre las pocas que aparecen, tenemos la ecuación
5x = 8. En las tablas en base sexagesimal hallaban el
recíproco de cinco que era 12/60 y en la tabla de
multiplicar por 8, encontramos 8 · 12/60 = 1
36/60

Los matemáticos griegos no tuvieron problemas con
las ecuaciones lineales y, exceptuando a Diophante (250 d. de
C.), no se dedicaron mucho al álgebra, pues su
preocupación era como hemos visto, mayor por la
geometría. Sobre la vida de Diophante aparece en los
siglos V o VI un epigrama algebraico que constituye una
ecuación lineal y dice:

Los primeros documentos matemáticos que existen
(datan del siglo III d. de C.) son los Sulvasütras, donde se
recogen todos los conocimientos necesarios para construir los
templos. En éstos aparece el siguiente
problema:

Esto es:

Es decir, a x = S.

Lo resolvían utilizando el método de la
falsa posición, como los egipcios.

Posteriormente, Brahmagupta (siglo VII) expresa, ya de
forma sincopada, cómo resolver ecuaciones lineales. La
incógnita la representaba por la abreviatura ya, y las
operaciones con la primera sílaba de las
palabras.

Dada la ecuación   ax + b = cx + d   ,
la solución vendrá dada dividiendo la diferencia de
los términos conocidos entre la diferencia de los
coeficientes de los desconocidos, esto es,

Estos métodos pasaron a los
árabes que los extendieron por Europa. Al algebrista
Abu-Kamil (siglo IX y X) se le atribuye una obra donde trata la
solución de ecuaciones lineales por simple y doble falsa
posición.El método de la doble falsa
posición es el siguiente:Sea la ecuación   ax
+ b = 0   y supongamos dos valores para la x
:      x = m
      am + b = p
      x = n
       an + b = q
restando,      a (m – n) = p – q Por
otra parte, eliminando a en (1)      
amn + bn = pn      amn + bm = qm que
restando,       b (n – m) = pn – qm y
dividiendo ambos resultados,       – a /
b = (p – q) / (pn – qm) o también
      – b / a = (pn – qm) / (p – q)
siendo esto último el valor de   x
&nbsp.

Veamos un ejemplo. Sea la ecuación
  5x – 10 = 0   , si tomamos como valor de x : x = 3 y
x = 4 , y sustituyendo,       5 ·
4 – 10 = p       5 · 3 – 10 = q
se tiene que       x = (10 · 3 –
5 · 4) / (10 – 5) = (30 – 20) / 5 = 10 / 5 = 2

Este principio fue posteriormente presentado en una
forma ligeramente modificada por el método de las escalas.
El nombre proviene de un diagrama que permitía escribir la
solución rápidamente:

Las dos líneas de la izquierda representan p y q
y las de la derecha m y n y la cruz del centro indica que hay que
multiplicar.

El método puede ser sintetizado como
sigue:

1. Consideran dos valores cualesquiera de
la incógnita m, n . 2. Calculan los errores
correspondientes a ellos p, q .3. Hallan el valor de la
incógnita en función de los valores dados y sus
errores.

En nuestro ejemplo,

A partir de aquí se dedican al estudio de
ecuaciones de grado superior.

• HISTORIA DE LOS SISTEMAS DE ECUACIONES
  LINEALES.

Los sistemas de ecuaciones lineales fueron ya resueltos
por los babilonios, los cuales llamaban a las incógnitas
con palabras tales como longitud, anchura, área, o volumen
, sin que tuvieran relación con problemas de
medida.

Un ejemplo tomado de una tablilla
babilónica plantea la resolución de un sistema de
ecuaciones en los siguientes términos:

1/4 anchura + longitud = 7
manos

Longitud + anchura = 10 manos

Para resolverlo comienzan asignando el
valor   5   a una mano y observaban que la
solución podía ser: anchura = 20, longitud = 30 .
Para comprobarlo utilizaban un método parecido al de
eliminación. En nuestra notación, sería: y +
4x = 28

y + x = 10

Restando la segunda de la primera, se
obtiene 3x = 18 , es decir, x = 6 e y = 4 . También
resolvían sistemas de ecuaciones, donde alguna de ellas
era cuadrática. Los griegos también
resolvían algunos sistemas de ecuaciones, pero uti1izando
métodos geométricos. Thymaridas (400 a. de C.)
había encontrado una fórmula para resolver un
determinado sistema de   n   ecuaciones con   n
  incógnitas. Diophante resuelve también
problemas en los que aparecían sistemas de ecuaciones,
pero transformándolos en una ecuación
lineal.

Diophante sólo aceptaba las
soluciones positivas, pues lo que buscaba era resolver problemas
y no ecuaciones. Utilizó ya un álgebra sincopada
como hemos señalado anteriormente. Sin embargo, unas de
las dificultades que encontramos en la resolución de
ecuaciones por Diophante es que carece de un método
general y utiliza en cada problema métodos a veces
excesivamente ingeniosos.

Los sistemas de ecuaciones aparecen también en
los documentos indios. No obstante, no llegan a obtener
métodos generales de resolución, sino que resuelven
tipos especiales de ecuaciones.

El libro El arte matemático , de autor chino
desconocido (siglo III a. de C.), contiene algunos problemas
donde se resuelven ecuaciones. En ellos encontramos un esbozo del
método de las matrices para resolver sistemas de
ecuaciones lineales. Uno de dichos problemas equivale a resolver
un sistema de tres ecuaciones lineales por dicho método
matricial.

• ECUACIONES DE V GRADO

En matemática, se denomina ecuación
quíntica o de quinto grado a una ecuación
polinómica en que el exponente de la variable
independiente de mayor grado es cinco. Es de la forma
general: