- Adición de números
naturales - Sustracción de números
naturales - Multiplicación de números
naturales - La
división en los naturales
ADICION DE
NUMEROS NATURALES
La adición o suma es una operación
fundamental utilizada para resolver problemas que implican
situaciones de cambio en donde se dé un incremento o
aumento, una igualación, o una
combinación.
Por ejemplo:
¿Cuánto, gana mensualmente un profesor si
recibe de sueldo base Q 1 236.00 y de prestaciones Q
568.00?
Manuel mide 132 cm pero si tuviera 47 cm más
tendría la estatura de su papá. ¿Cuál
es la estatura del papá de Manuel?
En el colegio Americano hay 250 alumnos y 235 alumnas.
¿Cuál es su población escolar en
total?
Cada uno de estos problemas se resuelve con una
adición, motivo por el cual se recordarán sus
términos y la forma en que se efectúa.
Obsérvense los términos y el
signo operacional de las siguientes adiciones:
Los sumandos son los números que se van a reunir
en uno solo llamado suma.
• La suma o total es el resultado de
la adición.

El signo + es el signo operacional
de la adición.
La adición puede registrarse en forma vertical o
en forma horizontal, como pudo observarse en las operaciones
anteriores. A continuación se explicará el
algoritmo o procedimiento para efectuar la
adición:
1. Para mayor comprensión se
efectúa en forma vertical se alinean las unidades de
cada sumando y automáticamente todas las cifras
quedarán alineadas por órdenes: unidades con
unidades, decenas con decenas, centenas con centenas,
etcétera.

2. Se inicia con la suma de las unidades de cada
sumando, su suma o total se registra abajo de la línea. Si
la suma es igual o mayor que 10 se descompone el número en
decenas y unidades y sólo se registran las unidades, y las
decenas resultantes se colocan en la columna de las decenas, como
ocurre en la segunda adición.

3. Se suman las decenas. Si la suma es igual o mayor que
10 se descompone nuevamente el número, ahora en centenas y
decenas. Obsérvese la segunda adición.

4. Se suman las centenas y se procede en forma
análoga si el resultado es 10 o mayor que
él.
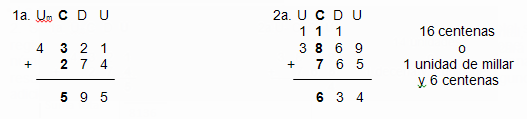
5. Se suman las unidades de millar en forma
semejante.

6. Si existen más órdenes se
continúa el mismo procedimiento.
Conforme se vaya adquiriendo habilidad, las estimaciones
se harán con mayor precisión y en forma mental. La
estimación del resultado permitirá pronosticarlo y
detectar errores de procedimiento.
Para ir adquiriendo práctica es fundamental que
practique en casa usted mismo efectuando diferentes problemas
matemáticos de sumas. Ejercicio no. 1

1. Los tomos de una enciclopedia tienen el
siguiente número de páginas: el primero 485, el
segundo 520 y el tercero 397, calcula el número de
páginas que tiene la obra, en total.
2. ¿Cuánto, gana
mensualmente un profesor si recibe de sueldo base Q 1 236.00
y de prestaciones Q 568.00?
3. Manuel mide 132 cm pero si tuviera 47 cm
más tendría la estatura de su papá.
¿Cuál es la estatura del papá de
Manuel?
SUSTRACCIÓN DE NÚMEROS
NATURALES
La sustracción o resta es otra operación
fundamental, y al igual que la adición, se utiliza para
resolver problemas de cambio, combinación,
igualación o comparación.
Ejemplos:
– En un tinaco de 500 litros de capacidad se han
depositado 186 litros de agua, ¿cuántos litros
necesita para llenarse?
– En un zoológico existen 1 238 animales
diferentes, de los cuales 105 son felinos. ¿Cuántos
animales existen en el zoológico que no son
felinos?
– Alfredo mide 169 cm y su sobrino Gerardo 87 cm,
¿cuántos centímetros le faltan a Gerardo
para tener la misma estatura de su tío Alfredo?
Cada uno de estos problemas se resuelve con una
sustracción. Obsérvense los términos y el
signo operacional de las sustracciones siguientes:

En la sustracción de números naturales, el
minuendo siempre debe ser mayor o igual al sustraendo, en caso
contrario, la resta no tendría solución dentro de
los números naturales.
El algoritmo de la sustracción es similar al de
la adición, pues deben restarse sólo las cifras del
mismo orden, iniciando con las unidades, sigue con las decenas,
después con las centenas, etcétera.
Cuando en la sustracción todas las cifras del
minuendo son mayores a las del sustraendo, no existe dificultad,
pues se efectúa como si fueran varias sustracciones de una
sola cifra.
Ejemplo:

La dificultad se presenta cuando el minuendo tiene
cifras menores a las cifras del sustraendo, (excepto la cifra del
orden mayor). Por ejemplo:

En este caso es necesario reagrupar, porque se necesitan
más unidades. Para esto, se considera la cifra del orden
inmediato superior: o dicho de otra manera se presta uno al
número de la izquierda y el 2 se transforma en 12. Y de
esta manera ya se puede realizar la operación de la resta.
Observe.

Obsérvese la siguiente sustracción
dónde hay más reagrupamientos:

Con práctica, los reagrupamientos se hacen
mentalmente sin necesidad de registrarlos.
La sustracción se verifica cuando el minuendo es
igual a la suma del sustraendo con la resta o diferencia.
Ejemplo:

Para ir adquiriendo práctica es fundamental que
practique en casa usted mismo efectuando diferentes problemas
matemáticos de restas.
Ejercicio no. 2

MULTIPLICACIÓN DE NÚMEROS
NATURALES
La solución de una adición donde los
sumandos son iguales, es decir, que se repiten, se puede obtener
de una forma directa y sencilla.
Por ejemplo:
Al calcular la cantidad de frascos de café que
hay en 9 docenas, se obtiene mediante la siguiente
adición:

En esta operación se repite 9
veces el doce como sumando, lo cual se puede representar con la
siguiente expresión:
9 veces 12 = 9 x 12
9 x 12 = 108; 108 frascos de café
hay en 9 docenas.
Esta operación recibe el nombre de
multiplicación y se define así: La
multiplicación es la suma abreviada con la cual se tiene
el resultado de dos o más sumandos iguales.
Los elementos que forman una multiplicación
son:

Para indicar esta operación se utiliza entre
otros el signo x que se lee "por", el cual se coloca entre los
números a multiplicar.
Ejemplo:
9 x 12 que se lee: nueve por doce.
También es correcto utilizar paréntesis,
por ejemplo:
(9) (12) que se lee: nueve por doce
Pero como realizar la multiplicación de
números naturales en aritmética. Veamos a
continuación. Debemos recordar que para una mejor
aplicación es fundamental ordenar a la
multiplicación de forma vertical.
Si queremos multiplicar la misma multiplicación
que fue citada anteriormente la representaremos
así:

Vamos paso por paso:
Cuando se efectúa en forma vertical se alinean
las unidades de cada factor y automáticamente todas las
cifras quedarán alineadas por órdenes: unidades con
unidades, decenas con decenas, centenas con centenas,
etcétera. Veamos este ejemplo:

Se inicia con la multiplicación de las unidades
de cada factor, el producto o total se registra abajo de la
línea. Si el producto o resultante es igual o mayor que 10
se descompone el número en decenas y unidades y
sólo se registran las unidades, y las decenas resultantes
se colocan en la columna de las decenas, como ocurre en la suma
de adición.

Se multiplican las decenas. Si el producto es igual o
mayor que 10 se descompone nuevamente el número, ahora en
centenas y decenas. Solo se registran las decenas y las centenas
resultantes se colocan en la columna de las centenas o dicho de
otra forma se escribe el 8 (tomando en cuenta que 27 y 1 que
llevamos nos da 28) entonces se anota el 8 y se coloca el 2 en la
parte de arriba de las centenas.

Se multiplica las centenas y se procede en este caso a
sumar al producto o resultante la cantidad que se encuentra en la
parte superior de la casilla de las centenas,
así:
9 X 1= 9 + 2= 11 y esa es la cantidad que debemos colar
como resultado final. Veamos.

Si existen más órdenes se continúa
el mismo procedimiento.
Pero que hacer cuando la multiplicación es un
poco mayor que esta.
Ejemplo:
132 X 99= ?
Se realiza los mismos pasos anteriores:

Solo que en este caso se corre una casilla al lado
izquierdo del primer resultado de la operación. Y luego se
realiza la sumatoria. (Como ya aprendimos a sumar no es necesario
explicar como se realiza la sumatoria). Debe quedar detallada
así.

Cuando se usan literales conviene utilizar
paréntesis o un punto en medio de los factores que indique
la multiplicación, de este modo se evita que el signo "x"
se confunda con la literal "x"; en ocasiones el punto se
puede omitir.
Ejemplo:

Para ir adquiriendo práctica es fundamental que
practique en casa usted mismo efectuando diferentes problemas
matemáticos de multiplicaciones. (Ejercicio 3).

MULTIPLICACIÓN DE UN
NÚMERO NATURAL POR 10, 100, 1 000,
ETCÉTERA
La comprensión de este tema
permitirá calcular el producto de un número natural
por 10, 100, 1 000, etcétera, de una forma rápida y
simple, sin necesidad de efectuar el algoritmo ya conocido de la
multiplicación.
Obsérvense los siguientes productos, donde uno de
los factores es un número natural y el otro 10, 100, 1
000, etcétera.

Nótese que cada uno de los productos está
formado por las mismas cifras del factor de la columna A,
a las cuales se le agregan tantos ceros como los haya en los
factores correspondientes de la columna B.
En los productos a) y d) se agregó
un cero a la derecha del factor multiplicado por 10,
así:
a) 27 x 10 = 270 y d) 311 x 10 =
3110
En los productos b) y e) se agregaron dos
ceros a la derecha del factor multiplicado por 100,
así:
b) 27 x 100 = 2 700 y e) 311 x 100 = 31 100
Nota:
El producto de un número natural por 10, 100, 1
000, etcétera, es igual al número natural seguido
de tantos ceros como tenga el número por el que se
multiplica.
Ejemplos:

Practica y aprende: (ejercicio No. 3)

LA
DIVISIÓN EN LOS NATURALES
Existe una operación que está relacionada
con la multiplicación: la división. Para apreciar
lo anterior, considera la siguiente situación.
Un alumno que cursa la secundaria requiere apoyos
económicos para continuar sus estudios. Por tal motivo,
consigue trabajo como empleado en una ferretería.
Después de trabajar siete días recibe Q 98.00.
¿Cuál es su sueldo diario?
Al analizar esta situación se nota que si se
multiplica el número de días trabajados 7,
por el sueldo de un día ( ? ), Se obtiene la cantidad
ganada 98 durante el lapso citado. Lo cual se puede
representar así:
7 x ( ? ) = 98
Es decir, se trata de una multiplicación en la
que se conoce el producto 98 y uno de los factores
7, mientras que se desconoce el otro factor, o
sea:

Al analizar una multiplicación en la que no haya
ninguna cantidad desconocida, se observa lo siguiente:
8 x 5 = 40 y como consecuencia:
40 entre 8 = 5 y 40 entre 5 =
8
En matemáticas esto se representa
como:

Dividir 98 ÷ 7, significa repartir
equitativamente las unidades del primer número entre cada
una de las unidades del segundo.
Como son 9 decenas y 8 unidades, se deben
repartir primero las decenas, que son de mayor valor, para que
cualquier sobrante (si lo hay) de las decenas, se aumente a las
unidades y se vuelva a realizar el reparto.
Así:

9 decenas entre 7, toca a 1 decena,
porque 7 x 1 = 7 y hay un sobrante de 2
decenas.

Como las 2 decenas sobrantes equivalen a
20 unidades y había 8 unidades, se tiene un
total de 28 unidades entre 7 y toca a 4
unidades. Dado que 4 x 7 = 28, ya no hay ningún
sobrante.

La división se puede definir
así:
La división es la operación en la cual,
dado un producto de dos factores y conociendo uno de ellos, se
busca el otro factor.
Desde ese punto de vista, la división es la
operación inversa de la multiplicación. Si se
considera que la mayoría de las divisiones se realizan con
números de 2 o más cifras (tanto en el
dividendo como en el divisor), lo más común es
presentarlas de la siguiete forma:

Cuando el residuo es 0, se trata, de una
división exacta.
Si el residuo es distinto de 0, como en el
siguiente ejemplo, la operación se llama
división entera o euclidiana.

El divisor no puede ser nunca 0, porque entonces
no hay solución.
Ejemplo:
4 ÷ 0 no tiene solución, porque no existe
ningún número natural que multiplicado por
0, dé como resultado 4.
Autor:
Cesar Gamboa