El algoritmo de Prim

A Elmer Coyla Idme, docente de
la

Universidad Nacional del Altiplano de
Puno

por brindarnos su enseñanza en este
año académico

PRESENTACION

La utilidad académica de una
monografía nunca está de más, el uso de esta
es una gran ayuda para estudiantes en este caso universitarios es
por eso que con esta recopilación de fuentes
científicas impresas mas las conclusiones llegadas al
tomar opinión de varios profesionales del área
hacen de esta monografía consistente en "el algoritmo de
Prim" una fuente de información más para fines
académicos.

En estos tiempos el estudiantado opta por
recurrir a fuentes sin sustento científico como el
internet o simplemente dar por hecho algún comentario sin
sustentación, ya sea con fines de curiosidad o estudiantes
trabajando en algún proyecto. El uso de los libros se
está perdiendo y con ello los libros mismos.

En esta monografía tocaremos el tema
principal que es "El Algoritmo de Prim", dando a conocer y a
repasar algunos puntos importantes en el área, como son
los grafos, los arboles, y los diferentes tipos de
términos que se usan en la teoría de grafos,
también veremos cómo influye tal algoritmo en la
vida cotidiana y cuan útil nos es…

INTRODUCCION

El hombre siempre ha tenido la necesidad de
recorrer muchos lugares, utilizando caminos estratégicos y
cortos buscando hallar la ruta optima con el mayor ahorro de
tiempo, energía, distancia, etc. recorriendo todos los
puntos designados.

En la actualidad podemos apreciar muchas
cosas que nos pueden parecer de lo más
habitual, caminos, líneas de comunicación
telefónica, televisión por cable, el transporte ferroviario,
líneas aéreas, circuitos eléctricos
de nuestras casas, automóviles, etc. ; lo que no
pensamos frecuentemente es que estos forman parte de algo que
en matemáticas se
denomina como grafos.

En esta monografía se explicara el
Algoritmo de Prim, buscando aplicarlo en problemas reales y
cotidianos, utilizando en general la Teoría de
Grafos.

RESUMEN

Un grafo o grafica es un conjunto finito de
nodos o vértices conectados a través de aristas,
los cuales pueden ser conexos, es decir existe algún
enlace con cada nodo a través de algún camino
formando así un grafo entero; O los grafos no conexos, que
tienen la particularidad de que un segmento de grafo no este
enlazado a través de algún vértice al grafo
principal. En la teoría de grafos existen grafos dirigidos
y grafos no dirigidos , lo grafos dirigidos son aquellos donde
sus aristas tienen un sentido , quiere decir que tienen un
principio especifico en algún nodo y un destino en
algún otro a diferencia de los no dirigidos que son solo
grafos simples (puede tomar ambas direcciones).

Arboles, un árbol es un grafo que no
contiene ciclos y que conecta todos los nodos utilizando el menor
número de aristas posibles.

Árbol recubridor mínimo,
dentro de un grafo se tiene que cubrir todos los nodos formando
un árbol (sub grafo) y utilizando el menor coste posible
(menor costo, tiempo, distancia, precio, etc.)

El algoritmo de Prim es un algoritmo de la
teoría de grafos que encuentra un árbol de
expansión mínima para un grafo ponderado
conexo. Esto significa que se encuentra un subconjunto de
las aristas que forma un árbol que incluye todos los
nodos, donde el total peso de todas las aristas en el
árbol se reduce al mínimo.  Si
el gráfico no está conectado, entonces
sólo se encuentra un mínimo  árbol de
expansión para uno de los componentes
conectados

ABSTRACT A graph or chart is a
finite set of nodes or vertices connected by edges, which can be
related, ie there is a link to each node through some path thus
forming a whole graph, or graphs are not related to are unique in
that a segment of the graph is not bound by a vertex to the main
graph. In graph theory there are directed graphs and undirected
graphs, the directed graphs are where its edges have a sense,
means they have a specific principle in a node and a destination
unlike any other non-target are only simple graphs (can take both
directions.)  Trees, a tree is a graph that contains no
cycles and connecting all the nodes using the fewest possible
edges.

Minimum spanning tree within a graph has to
cover all the nodes forming a tree (sub graph) and using the
lowest possible cost (less cost, time, distance, price, etc)
Prim's algorithm is an algorithm of graph theory that finds a
minimum spanning tree related to a weighted graph. This means
that there is a subset of edges forms a tree with all nodes,
where the total weight of all edges in the tree is minimized. If
the graph is not connected, then it is only a minimum spanning
tree for a connected component

PROLOGO

Mediante esta monografía tenemos
como objetivo principal que los lectores cuenten en forma integra
con los alcances más relevantes del Algoritmo de Prim
considerando la teoría de grafos teniendo en cuenta que el
estudio de los diferentes tipos de algoritmos cada vez tiene
más importancia en la medida que avanza la era de las
computadoras, caminos, líneas de comunicación
telefónica, televisión por cable,
el transporte ferroviario, líneas
aéreas, circuitos eléctricos de nuestras
casas, automóviles Y que se puede resolver diferentes
tipos de problemas utilizando dicho algoritmo. Teniendo la
ventaja de ahorrar tiempo y costos al resolver un problema
determinado.

El trabajo, ha sido elaborado siguiendo una
metodología dinámica, propia del grupo, lo cual
garantiza a nuestros lectores un ágil manejo y acceso a la
información que desee consultar.

CAPITULO I

CONCEPTOS
PREVIOS

• Grafos.

ELIAS MICHA
(2003)[1], En su libro Matemáticas
Discretas este autor:

"Un grafo es un conjunto no vacio de
objetos llamados vértices y de un conjunto de parejas no
ordenadas de vértices llamadas Aristas."

SEYMOUR LIPSCHUTZ – MARC LIPSON
(2007)[2], En su libro Matemáticas
Discretas Indica:

"Un grafo tiene un numero finito de
vértices y de aristas."

BERNARD KOLMAN – ROBERT C. BUSBY
– SHARON ROSS (1995)[3], En su libro
Estructuras Matemáticas Discretas nos dice:

"Un grafo G consta de un conjunto V
de objetos llamados vértices, un conjunto finito E de
objetos llamados aristas y una función "y" que
asigna a cada arista un subconjunto {v, w}, donde "v, w" son
vértices (que podrían ser iguales)."

• Conectividad

ELIAS MICHA (2003), ""Un Grafo es
conexo si consiste de una sola pieza. Es decir que los
vértices están unidos a través de
aristas."

SEYMOUR LIPSCHUTZ – MARC LIPSON
(2007), "Un Grafo de conectividad consta de una secuencia
alternada de vértices y aristas de la forma donde cada
arista contiene a los vértices."

Por lo tanto concluimos que la
conectividad de un grafo es el enlace que puede tener 2 nodos a
travez de uno o más aristas.

• Grafos Dirigidos y no dirigidos.

JIRÍ MATOUŠEK, JAROSLAV
NEŠETRIL(2008) [4]En su libro
Invitation to Discrete Mathematics nos dice:

"Un grafo dirigido G es un par (V,E), donde
E es un subconjunto del producto cartesiano VxV. A los pares
ordenados(x,y) ? E se les llama ramas dirigidas. Decimos que una
rama dirigida e=(x,y) tiene origen x y por final y, o
también decimos que es una rama de x a y."

ROBERT SEDGEWICK (1992)
[5]En su libro Algoritmos en C++ nos
dice.

" Un grafo no dirigido, la conectividad
simple proporciona los vértices que pueden ser alcanzados
desde un vértice dado recorriendo los aristas del
grafo."

• Arboles.

Es un grafo que no tiene ciclos y que
conecta a todos los puntos,. En un grafo
con n vértices, los árboles tienen
exactamente n – 1 aristas, y
hay nn-2 árboles posibles. Su importancia radica
en que los árboles son grafos que conectan todos los
vértices utilizando el menor número posible de
aristas.

• Árbol Recubridor
  Mínimo.

BERNARD KOLMAN – ROBERT C. BUSBY
– SHARON ROSS (1995)[6], En su libro
Estructuras Matemáticas Discretas para la
computación señala:

"Dado un grafo conexo,
un árbol recubridor mínimo de ese grafo
es un subgrafo que
tiene que ser un árbol y
contener todos los vértices del
grafo inicial. Cada arista tiene asignado un peso proporcional
entre ellos, que es un número representativo de
algún objeto, distancia, etc., y se usa para asignar un
peso total al árbol recubridor mínimo computando la
suma de todos los pesos de las aristas del árbol en
cuestión. Un árbol recubridor
mínimo o un árbol expandido
mínimo es un árbol recubridor que pesa menos o
igual que otros árboles recubridores. Todo grafo tiene
un bosque recubridor mínimo."

CONCLUSION

Grafo. Es el conjunto de vértices y
aristas, los cuales, se representa gráficamente como un
conjunto de puntos llamados nodos y las aristas se representan
por líneas o puentes que unen dichos nodos

La teoría de grafos sirve como un
modelo matemático para estructuras en cualquier campo ,
pero una de las mas importante en las aéreas de ciencias
de la computación .

Árbol. Un árbol se define
como un tipo de grafo que no contiene ciclos, es decir es un
grafo acíclico y a su vez es conexo. Quiere deciry que
conecta a todos los puntos,. En un grafo con n vértices,
los árboles tienen exactamente n – 1 aristas, y hay nn-2
árboles posibles. Su importancia radica en que los
árboles son grafos que conectan todos los vértices
utilizando el menor número posible de aristas.

CAPITULO II

ALGORITMO DE
PRIM

ROSA GUEREQUETA GARCIA – ANTONIO
VALLECILLO MORENO (2004)[7], En su libro
Técnicas de Desarrollos de Algoritmos nos dice:

"El algoritmo de Prim es tal vez el
algoritmo de MST (Arboles Generadores Mínimos) más
sencillo de implementar y el mejor método para grafos
densos. Este algoritmo puede encontrar el MST de cualquier grafo
conexo pesado.

Sea V el conjunto de nodos de un
grafo pesado no dirigido. El algoritmo de Prim comienza cuando se
asigna a un conjunto U de nodos un nodo inicial
Perteneciente a V, en el cual "crece" un árbol de
expansión, arista por arista. En cada paso se localiza la
arista más corta (u, v) que conecta a U
con V-U, y después se agrega v, el
vértice en V-U, a U. Este paso se repite
hasta que V=U. El algoritmo de Prim es de O(N2), donde |
V | = N.

El siguiente ejemplo ilustra el
funcionamiento del algoritmo.

La secuencia de ilustraciones va de
izquierda a derecha y de arriba hacia abajo. La primera imagen
muestra el grafo pesado y las siguientes muestran el
funcionamiento del algoritmo de Prim y como va cambiando el
conjunto U durante la ejecución.

Figura 1

Agregar un nodo al MST es un cambio
incremental, para implementar el algoritmo de Prim debemos
enfocarnos en la naturaleza de ese cambio incremental. La clave
está en notar que nuestro interés esta en la
distancia más corta de cada vértice de U a
V-U.

Al U agregar un nodo v al
árbol, el único cambio posible para cada
vértice w fuera del árbol es que agregar
v coloca a w más cerca del árbol.
Esto no es necesario verificar la distancia de w a todos
los demás nodos del árbol, solo se necesita
verificar si la adición de v al árbol
necesita actualizar dicho mínimo. Esto se puede lograr
agregando una estructura de datos simple para evitar repetir
cálculos excesivos, y hacer que el algoritmo sea
más rápido y más simple.

El siguiente ejemplo ilustra la
metodología anterior, utilizando una pila de aristas P, en
donde las aristas se van apilando en menor a mayor según
el peso de la misma. La secuencia de ilustraciones va de
izquierda a derecha.

Figura 2

Se comienza en el nodo 0 y se apilan las
aristas adyacentes a este nodo, en orden decreciente. La arista
mínima es la que está en el tope de la pila,
así que se des apila y se agrega al MST.

Seguidamente se procede con el nodo 1 y se
apilan sus aristas adyacentes, con la diferencia de que hay que
verificar si dichas aristas representan un nuevo camino
mínimo con respecto a las aristas que ya están
introducidas en la pila. En este caso no se apila la arista 1-3
porque ya hay una arista que lleve a 3 con el mismo costo en la
pila. Se toma 1-2 porque está en el tope y se procede con
el nodo 2. Cuando se va a apilar la arista 2-3, se encuentra que
ya hay un camino que lleve a 3 pero de mayor costo, así
que se desopila 0-3 y luego se apila 2-3. Se agrega 2-3 al MST y
termina el proceso, porque el conjunto de nodos en el MST es
igual al conjunto de vértices del grafo
original."

ALFREDO CAICEDO BARRERO, GRACIELA WAGNER
DE GARCÍA, ROSA MARÍA MÉNDEZ PARRA
(2010)[8], En su libro Introducción a
la Teoría de Grafos dice:

"Supóngase N = {1, 2, 3,…,n}.
El algoritmo de Prim comienza con un conjunto U inicializado con
cualquier nodo, por ejemplo {1}. Luego se hace crecer un
árbol generador, arco por arco. En cada paso se encuentra
el arco más corto (u, v) que conecta a U y N – U y
luego se adiciona v, el nodo en N – U, a U. Se repite este
paso hasta que U = N

El algoritmo es resumido en los siguientes
pasos:

Algoritmo de PRIM.

Paso 0. Iniciar el grafo T con un solo nodo
i escogido al azar: N = {i}, A = 0, T = ({i},0)

Paso 1. Seleccionar el arco (i, j) cuya
longitud es la menor entre todos aquellos arcos adyacentes a T.
Adicionar este arco (i,j) a T y j al conjunto de nodos de
T

Paso 2. Preguntar si T ya es un
árbol que contiene todos los nodos de G y detenerse. En
este caso contrario repetir el paso 1"

CONCLUSION

El algoritmo de PRIM es un método
para poder hallar un árbol recubridor mínimo en un
grafo aciclico conexo no dirigido que nos permita hallar en un
grafo el coste mínimo para una serie de
actividades.

CAPITULO III:

Aplicación del
Algoritmo de Prim

Este algoritmo se usa normalmente para
ahorrar recursos, su aplicación mas común es la
implementación de cables de redes, de servidores, de
postes de luz entre otros.

Es decir el Algoritmo de Prim sirve para
poder hallar el "árbol recubridor mínimo", en un
grafo conexo no dirigido.

Ejemplos

Aplicando el algoritmo de Prim en un
problema de la vida real:

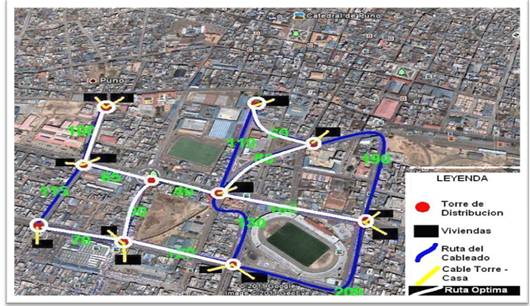
Situación: Implementación del
cableado para el servicio de televisión por cable en
ciertos puntos de un sector de la ciudad de Puno.

Problema: Ahorrar la mayor cantidad de
cable (recursos) en los puntos estratégicos (torres de
distribución) para llegar a todos los destinos
deseados.

Datos: Distancia entre torres y casas es de
10 metros (cada casa)

Planteamiento: En el figura 3 se observa la
ubicación de las torres de distribución y las
viviendas

Figura 3

En la figura 4 transformamos el conjunto de
torres y viviendas en un Grafo.

Figura 4

En la figura 5 Aplicamos el Algoritmo de
Prim en el grafo para hallar el árbol recubrir
mínimo o en otras palabras la ruta optima para ahorra la
distancia del cableado.

Figura 5

BIBLIOGRAFÍA

• Alfredo Caicedo Barrero, Graciela
  Wagner De García, Rosa María Méndez
  Parra (2010) Introducción a la Teoría de Grafos
  (2da ED)

• Bernard Kolman – Robert c. Busby
  – Sharon Rross (1997) Estructura

Matematicas Discretas (2da ED).
Francia.

• ELIAS MICHA (2003).Matematicas
  Discretas (2ta ED). Mexico.

• Jirí Matoušek,Jaroslav
  Nešetril(1998) Invitation to Discrete Mathematics (1ra
  ED) EE:UU.

• Rosa Guerequeta Garcia – Antonio
  Vallecillo Moreno (2004) Tecnicas de Desarrollos de
  Algoritmos (1ra ED)

• Robert Sedgewick (1992) Algoritmos en
  C++ (1ra ED) EE.UU

• Seymour Lipschutz – Marc Lipson
  (2007). Matematicas Discretas (3ra Ed)

Autor:

Alexander Flores
Mamani 

[1] ELIAS MICHA (2003).Matematicas Discretas
(2ta ED). Mexico. PAG. 22, 19

[2] Seymour Lipschutz – Marc Lipson
(2007). Matematicas Discretas (3ra Ed) PAG 158, 159

[3] Bernard Kolman – Robert c. Busby
– Sharon Rross (1997) Estructura Matematicas Discretas
(2da ED). Francia. PAG. 198

[4] Jirí Matoušek,Jaroslav
Nešetril(1998) Invitation to Discrete Mathematics (1ra
ED) EE:UU. PAG. 124,

[5] Robert Sedgewick (1992) Algoritmos en C++
(1ra ED) EE.UU PAG 277

[6] Bernard Kolman – Robert C. Busby
– Sharon Ross (1995) Estructuras de Matemáticas
Discretas para la Computación (3ra ED) Pag 321

[7] Rosa Guerequeta García –
Antonio Vallecillo Moreno (2004) Técnicas de Desarrollos
de Algoritmos (1ra ED) Cap 4 Pag 10

[8] Alfredo Caicedo Barrero, Graciela Wagner
De García, Rosa María Méndez Parra (2010)
Introducción a la Teoría de Grafos (2da ED)
Pág. 109