Secciones Cónicas y sus Aplicaciones (página 2)

Es el lugar geométrico de los puntos de un plano
que equidistan de un punto ubicado en el mismo plano denominado
centro. La distancia del centro a cualquier punto se denomina
radio

Centro: C(a; b)

Radio: r

–Ecuaciones de la
circunferencia

Circunferencia con centro en el punto (a, b)

Circunferencia con centro en el origen.

Ejemplo: Graficar:

Parábola:

Es el lugar de los puntos de un plano que equidistan de
un punto y de una recta del mismo plano. El punto se denomina
foco y la recta directriz.

-Componentes de la parabola

Foco:Es el punto fijo de F.

Directriz:Es la recta fija d.

Parametro: Es la distancia del foco a la dirtectriz,se
designa por la letra p.

Eje: Es la recta perpendicular a la directriz que pasa
por el foco.

Vertice:Es el punto d einterseccion de la parabola con
sus eje.

Radio vector: Es un segmento que une un punto cualquiera
de la parabola con el foco.

–Ecuaciones

(Dependiendo si es vertical u horizontal)

Parabola verticalel signo ("mas" o "menos") dirá si la abertura es
hacia arriba o abajo.

Parabola horizontal el signo
dirá si la abertura es hacia derecha o izquierda
respecto.

Ejemplo

Elipse:

Es el lugar geométrico de los puntos de un plano
cuya suma de distancias a dos puntos fijos del mismo es
constante. Los puntos fijos denominan focos.

-Componentes de la elipse

Focos: Son los puntos fijos F y F'.

Eje focal: Es la recta que pasa por los
focos.

Eje secundario: Es la mediatriz del segmento
FF'.

Centro: Es el punto de intersección de los
ejes.

Radios vectores: Son los segmentos que van desde un
punto de la elipse a los focos: PF y
PF'.

Ejes de simetría: Son las rectas que contienen al
eje mayor o al eje menor.

Centro de simetría: Coincide con el centro de la
elipse, que es el punto de intersección de los ejes de
simetría.

-Relación entre la distancia focal y los
semiejes

-Excentricidad de la elipse

La excentricidad es un número que mide el mayor
o menor achatamiento de la elipse. Y es igual al cociente entre
su semidistancia focal y su semieje mayor.

-Ecuaciones de la elipse

Elipse con centro en el punto (h; k)

Elipse con centro en el origen.

Ejemplo:

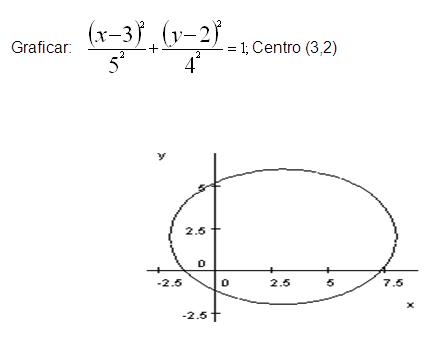
Ejemplo:

Hipérbola

Es el lugar geométrico de los puntos de un plano
tal que la diferencia de sus distancias a dos punto fijos del
mismo plano es constante. Los puntos fijos se llaman
focos.

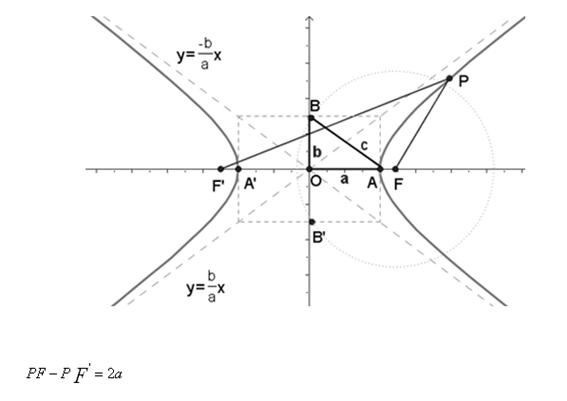
-Componentes de la
hipérbola

Focos: Son los puntos fijos F y
F'.

Eje focal: Es la recta que
pasa por los focos.

Eje secundario o
imaginario:

Centro: Es el punto de
intersección de los ejes.

Vértices: Los puntos A y A'
son los puntos de intersección de la hipérbola con
el eje focal.

Los puntos B y B' se obtienen como
intersección del eje imaginario con la circunferencia que
tiene por centro uno de los vértices y de radio
c.

Radios vectores: Son los segmentos
que van desde un punto de la hipérbola a los focos: PF y
PF'.

–Excentricidad de la
hipérbola

La excentricidad mide la abertura mayor o
menor de las ramas de la hipérbola.

-Ecuaciones de la
hipérbola

Ejemplo:

Aplicaciones de las
secciones cónicas

Las cónicas poseen curiosas e
interesantes propiedades por las que resultan sumamente
útiles en la naturaleza, la ciencia, la técnica o
el arte. Resumimos a continuación las diferentes
aplicaciones que las secciones cónicas tienen en la vida
real:

1. Una de las propiedades más utilizadas
de las parábolas es la de reflexión. En
Física se define una superficie reflectora cuando un rayo
incidente y el correspondiente rayo reflejado forman
ángulos iguales con la normal a la superficie. Un espejo
plano es un ejemplo de superficie reflectora. Otro ejemplo es, si
una parábola gira alrededor de su eje engendra una
superficie reflectora. Tiene la propiedad especial de que todos
los rayos que parten del foco, al chocar con la superficie se
reflejan todos paralelos entre sí al eje. Esta propiedad
es la base para la construcción de los espejos
parabólicos de los telescopios, los faros, las reflectoras
de ondas eléctricas y conchas acústicas de
micrófonos selectivos.

2. Los cables de los puentes colgantes tienen
forma parabólica (forman la envolvente de una
parábola). Se creía hace tiempo que las cuerdas o
cadenas que se suspenden agarradas únicamente por sus
extremos también formaban parábolas (hoy sabemos
que la curva que describen es un coseno
hiperbólico).

3. Las trayectorias de los proyectiles tienen
forma parabólica. Los chorros de agua que salen de un
surtidor tienen también forma parabólica. Si salen
varios chorros de un mismo punto a la misma velocidad inicial
pero diferentes inclinaciones, la envolvente de esta familia de
parábolas es otra parábola (llamada en
balística parábola de seguridad, pues por encima de
ella no es posible que pase ningún punto de las
parábolas de la familia). El mayor alcance que se puede
obtener es aquel en que el ángulo de inclinación
inicial es de 45 grados.

4. La forma de los telescopios, detectores de
radar y reflectores luminosos son parabólicas. En los
faros de los coches se coloca la fuente de luz en el foco de la
parábola, de modo que los rayos, al reflejarse en la
lámpara, salen formando rayos paralelos. La nave espacial
PLUTO de la NASA incorpora también un reflector
parabólico. Recordar también el conocido efecto de
quemar una hoja de papel concentrando los rayos solares mediante
un espejo parabólico.

5. Un telescopio de espejo líquido es un
telescopio reflectante (es decir, que usa la propiedad
reflectante de la parábola) cuyo espejo principal
está hecho de mercurio líquido. Un famoso ejemplo
lo constituye el telescopio HUBBLE situado en el espacio
exterior. El problema es cómo puede un líquido
formar un espejo parabólico y por qué se quiere
así. La respuesta es que si se tiene un contenedor
giratorio de líquido, la superficie del mismo formara un
paraboloide perfecto, incluso si la superficie interior del
contenedor tiene imperfecciones. De este modo, no es necesario el
pulido de los lentes y además los espejos pueden hacerse
más grandes que los sólidos. Al utilizar mercurio
líquido se consigue que los espejos sean más
baratos que los tradicionales (sólo hace falta una capa
muy fina de mercurio pues este es muy pesado).

6. Las secciones cónicas también
son aplicables a la mecánica celeste, esto fue descubierto
por Johannes Kepler, ya que las trayectorias que describen las
órbitas planetarias corresponden precisamente a las
secciones cónicas, las orbitas de los planetas alrededor
del sol son elípticas (el sol se encuentra en uno de los
focos). La excentricidad de la ´orbita de la Tierra
alrededor del Sol es aproximadamente 0,0167. La de mayor
excentricidad es la ´orbita de Plutón, 0,2481, que
incluso es pequeña. Los cometas y los satélites
también describen orbitas elípticas. En el extremo
contrario está el cometa HALLEY cuya excentricidad es de
0,9675, muy próxima a 1.

7. Otra aplicación se da al planear el
despegue de una nave espacial, ya que para que esta pueda
abandonar la tierra e ir a algún planeta (por ejemplo
Marte) tiene que encontrarse la tierra en algún punto de
la excentricidad correspondiente a la órbita
elíptica descrita por la tierra

8. En Óptica y propagación de ondas
se utilizan lentes elípticas.

9. En el área de la mecánica,
específicamente la dinámica del cuerpo
rígido son importantísimas las parábolas,
elipse y demás trayectorias, ya que para el
análisis cinemático de un mecanismo (por ejemplo el
diseño de levas) estas pueden describir una trayectoria
elíptica o de otro tipo, donde son aplicadas las
ecuaciones correspondientes a dichas figuras, también se
aplican las ecuaciones que rigen a las secciones cónicas
al describir el movimiento de un proyectil (tiro
parabólico),

10. En diseño artístico es
común encuadrar retratos y fotografías en un marco
con forma elíptica. La mayoría de los dispositivos
usados para recortar figuras elípticas están
basados en las ecuaciones de la elipse como comentamos
anteriormente.

11. Una revolucionaria técnica
médica introducida a mediados de la década pasada
para el tratamiento de los cálculos renales utiliza
propiedades reflexivas de las cónicas. La idea principal
consiste en usar ondas sonoras intensas generadas fuera del
cuerpo del paciente para pulverizar las piedras y convertirlas en
arena que pueda ser fácilmente eliminada por el organismo.
La clave está en enfocar las ondas para que no afecten al
cuerpo, solo al cálculo. Para ello se usa una
cámara semielipsoidal. En uno de sus focos se crea una
poderosa chispa que evapora agua. La parte que golpea el
reflector converge en el otro foco, donde se encuentra la piedra,
con toda su intensidad, provocando su destrucción. La
mejor cura para un cálculo es un poco de cálculo.
Este tratamiento se aplica en la actualidad en más del 80%
de piedras en el riñón y la uretra. Además
el tiempo de recuperación es de 3 días en
comparación con las dos semanas con la cirugía
convencional.

Conclusión

Las secciones cónicas influyen en lo que es el
aparato sensitivo del hombre, ya que nosotros dependemos de
nuestra capacidad de percepción, para poder trabajar con
ellas, en campos como la astronomía, la
aerodinámica, la geometría proyectiva, en
arquitectura, etc.

En cuanto a la astronomía las curvas
cónicas son importantes ya que cuando dos cuerpos masivos
interactúan según la ley de gravitación
universal, sus trayectorias describirán secciones
cónicas si su centro de masa se considera en reposo. Si
están relativamente próximas describirán
elipses, si se alejan demasiado describirán
hipérbolas o parábolas.

También son importantes en aerodinámica y
en su aplicación industrial, ya que permiten ser repetidas
por medios mecánicos con gran exactitud, logrando
superficies, formas y curvas perfectas.

Autor:

Mondragón Chavarria Karla
Xuxa