Desarrollo y aplicación de la metodología de cálculo de las fuerzas en los muñones de apoyo del cigüeñal (página 2)
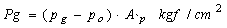
(1)
pg– Fuerza provocada por el gas en la cabeza del
pistón, pg– presión del gas en el cilindro,
po–presión en el interior del
cárter.
Esta fuerza se transmite se transmite a través de
la biela hasta el muñón de biela del árbol
cigüeñal. De las ecuaciones de equilibrio de la biela
Fig. 1. Se obtiene:
Estas fuerzas según la Teoría General de las
Máquinas Reciprocantes se pueden calcular por las
siguientes expresiones:
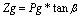
(2)
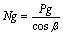
(3)
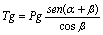
(4)
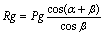
(5)

a) b)
Fig.1 a) Fuerzas provocadas por la presión del gas
pg.
b) Fuerzas provocadas sobre el árbol
cigüeñal por la fuerza de inercia Pi.
En los apoyos del árbol aparece la
reacción Ng" que puede ser descompuesta en Pg" y Zg" o en
Rg" y Tg".
El momento torsor provocado por la fuerza tangencial o
circunferencial Tg será:

(6)
Un momento de igual magnitud que está formado por
las fuerzas Zg y Zg" se transmite al bastidor del motor. El
momento reactivo es de signo contrario. Durante el movimiento de
los elementos del mecanismo manivela – biela –
pistón se generan fuerzas y pares de inercia, cuyo
cálculo se realiza por las conocidas
ecuaciones:

(7)

(8)
El signo menos indica que estas fuerzas son contrarias a
las respectivas aceleraciones. En estas expresiones:
m– masa, j –momento de inercia de masa.,
 aceleración
aceleración
lineal del centro de masa.,  aceleración angular del
aceleración angular del
elemento.
La biela tiene un movimiento complejo, de aquí
que para los cálculos de las fuerzas de inercia su masa se
considera reducida en dos masas equivalentes concentradas en la
cabeza y pie Fig. 1 b) cuyas magnitudes son:

(9)

(10)
Generalmente:  y
y 
Pesando por separado la cabeza de la biela tratando de
mantener el otro apoyo como articulado se obtuvieron los valores:
Wpb= 2.5 kgf, Wcb= 1.15 kgf. , Wb= 3.65 kgf.

Fig. 2 Esquema del pesaje de la
biela
Haciendo una sumatoria de momentos en A:

(11)
La longitud total de la biela de centro a centro de los
muñones del pasador del pistón al del
cigüeñal es L = 30 cm. Despejando de la sumatoria de
momentos (11) Lp se obtiene entonces:

La fuerza de inercia Pi provoca sobre el mecanismo son
fuerzas similares a las que provoca Pg las cuales se calculan por
las mismas fórmulas de Zg y Rg sustituyendo en ellas Pg
por Pi y que se designan respectivamente por Zi, Ni, Ti y Ri
Fig.1 b). También se provoca un par de inercia cuya
magnitud es:

(12)
En el muñón de la manivela del
cigüeñal se produce además la siguiente fuerza
de inercia.

(13)
Donde:
mm– masa del muñón de la
manivela.
También actuará la fuerza de inercia de
los cachetes

(14)
Donde: mc – masa del cachete, Rc– el radio
del centro de masa del cachete.
Los contrapesos del árbol cigüeñal
provocan fuerza de inercia también.

(15)
Donde: mCP– masa del contrapeso, Rcp– radio
de centro de masa del contrapeso.
Las fuerzas Tt y Rt resultantes se calculan para cada
instante de tiempo por las expresiones:

(16)

(17)
El momento torsor en la sección (i +1)
será:

(18)
En la Fig. 3 a) se muestra el esquema donde aparecen
todas las fuerzas que actúan sobre le cigüeñal
del compresor, que son:
Ax, Ay, Bx, By – Las reacciones en los cojinetes
de apoyo A y B.
R1, R2, R3, R4, R5, R6 – Las componentes radiales
de las fuerzas que le transmiten las bielas a cada uno de los
pistones del compresor.
T1, T2, T3, T4, T5, T6 – Las componentes
tangenciales de las fuerzas que le transmiten las bielas a cada
uno de los pistones del compresor.
S1, S2 – Fuerzas que le transmiten las correas de
la transmisión al cigüeñal.

a) b)
Fig. 3 a) Esquema de análisis del
cigüeñal del compresor. b) Ubicación de los
cilindros del cigüeñal del compresor
MYCOM.
El cigüeñal del compresor MYCOM – 6WB
posee una construcción muy peculiar. Posee solo dos codos
y a cada uno de los codos se conectan las bielas de tres
pistones. Los cilindros están separados un ángulo
de 60O entre sí como se ve en la Fig. 3 b).
Como ecuación que caracteriza esta ley de
variación se propone en el presente trabajo la
siguiente:

(19)
De manera que para:

Para los restantes pistones para una posición
angular a del cigüeñal, debido al desfasaje entre los
cilindros se cumplirán las siguientes expresiones para la
presión:

(20)
Las ecuaciones (19) y (20) han sido deducidas en el
presente trabajo para las características
específicas del cigüeñal analizado y no
están reflejadas en la literatura consultada. En la Fig. 4
se muestra un esquema donde se ubica la posición de los
pistones cuyas bielas están acopladas al
muñón superior y al muñón inferior
del cigüeñal.
 a) b)
a) b)
Fig. 4 Posición relativa de los
pistones y las bielas acopladas a) Al muñón
superior. b) Al muñón inferior del
cigüeñal
Las fuerzas Pg1, Pg2, y Pg3 serán:

(21)
Donde: P1– Sera la presión uno y Ap =
 – Área
– Área
del pistón Las fuerzas Zg1, Zg2, Zg3 y Ng1, Ng2 y Ng3
serán:

(22)

(23)
La relación entre un ángulo ßi y el
ángulo ai se relacionan entre sí de la siguiente
manera:

(24)
Donde: R– radio del cigüeñal, L–
longitud de la biela. Los ángulos ai se relacionan de la
siguiente manera:

La fuerza Tg será:

(25)
La fuerza Rg será:

(26)

Fig.5 Posición relativa de los
pistones y las bielas acopladas
al muñón inferior del
cigüeñal.
En la Fig. 5 se muestra un esquema donde se aplica la
posición relativa de los pistones cuyas bielas
están acopladas al muñón inferior I del
cigüeñal. De la misma forma que en el caso anterior
los ángulos ai y ßi se relacionan como  (27)
(27)
Los ángulos ai se relacionan entre sí de
la siguiente manera:

(28)
Las fuerzas Pg4, Pg5, Pg6 serán:

(29)
Las fuerzas Tg" y Rg" serán:
 (30)
(30)
La fuerza de inercia equivalente en el
muñón superior de la biela es:

(31)
Donde: mp – masa del pistón (Kg.)  aceleración del
aceleración del
pistón
La aceleración del pistón se obtiene del
análisis cinemático del mecanismo (Birger,
1986)

(32)
Donde: w – velocidad angular de la manivela,
R– radio del cigüeñal, L-longitud total de la
biela.
Después de obtener las fuerzas de inercia
correspondientes a cada pistón Pi1, Pi2, Pi3, Pi4, Pi5,
Pi6. Se pueden hallar las fuerzas Ti" y Ri" y hallamos
también Tg" y Rg".

(33)

(34)
El cálculo de las Fuerzas en la
transmisión por correas se realizó por las
ecuaciones clásicas del cálculo de las
Transmisiones por Correas (Dobrovolski, 1975; Iusilievich, 1988;
Ivanov, 1991).
El ángulo a es:
 y
y
 (35)
(35)


Donde: Dp1 y Dp2 – diámetros primitivos de
las poleas, A – Distancia entre centros.

(36)
Donde: Dp– diámetro primitivo de la polea,
c– dimensión nominal de la ranuras de la
polea
Para el cálculo se necesita el Dp1, 2, de la
ecuación anterior:
 y A=143
y A=143
cm
El torque en el eje de motor, para la potencia y la
velocidad de giro del compresor MYCON es:

 (37)
(37)
Donde: Nm– Potencia del motor en kW, nmin –
velocidad de giro mínima del motor.
El troque en el eje del compresores:

(38)
 Donde:
Donde:
 y ?corr ~
y ?corr ~
0.96
El torque en el eje del compresor también es igual
también a:
 (39)
(39)
Se conoce también que el coeficiente de empuje se
calcula como: 
(40)
Para correas trapezoidales f= 0.7 – 0.9.se toma entonces
un valor medio de f = 0.8.

(41)
Las fuerzas sobre el árbol, horizontal y vertical
serán:


(42)
Fig. 6 a) Esquema de las Fuerzas sobre el
Árbol b) Reacciones en los Muñones de
Apoyo

(43)

(44)
 (45)
(45)
Las reacciones resultantes en A y B
serán:

(46)
Las ecuaciones anteriores fueron programadas en EXCEL. A
continuación se muestran los gráficos obtenidos
donde se observa cómo se comportan los parámetros
de presión, fuerza del gas, fuerza de inercia y las
reacciones en los apoyos, RA y RB con relación al
ángulo de giro del cigüeñal para la velocidad
mínima de operación n = 650 rpm.

Fig. 7. Gráfico del comportamiento
de la fuerza a) Del gas sobre los pistones en kgf v.s.
ángulo de giro del cigüeñal. b) De inercia en
kgf v.s. ángulo de giro del
cigüeñal.

Fig. 8 a) Gráfico de la reaccion
RA en kgf. b) Gráfico de la reacción RB, en kgf
contra ángulo de giro del cigüeñal para
velocidad mínima del cigüeñal.
Como se aprecia las reacciones no tienen valores
estables. La reacción máxima se observa en el apoyo
B que es el del lado del motor y tiene un valor máximo de
2 971.82 kgf, que fue precisamente el apoyo averiado. Con estas
fuerzas sobre los muñones se aplicaron las condiciones de
optimización de la lubricación para poder
establecer las insuficiencias de ésta.
CONCLUSIONES
De los resultados del trabajo se obtuvieron las
siguientes conclusiones. Se dedujeron las ecuaciones que
caracterizan el comportamiento de la presión en cada
pistón tomando en cuenta el comportamiento individual y el
desfasaje entre los pistones, las ecuaciones que caracterizan el
comportamiento de la fuerza del gas, la fuerza de inercia y la
superposición de estas fuerzas con las de las correas para
mediante el equilibrio poder obtener para el compresor MYCON 6WB
las reacciones en los puntos de apoyo del cigüeñal.
Se procesaron las ecuaciones anteriores para los datos del
compresor MYCON 6WB y se obtuvieron los gráficos de
comportamiento de la presión de cada pistón y del
compresor, la fuerza del gas, la fuerza de inercia y las
reacciones en los puntos de apoyo A y B para las velocidades de
giro máxima y mínima del compresor. Las reacciones
en los apoyos resultan inestables durante el giro del
cigüeñal tanto para el apoyo A como para el B y la
reacción máxima se produce siempre en el apoyo B,
RBmax = 2 971.82 kgf que fue precisamente el apoyo
averiado.
BIBLIOGRAFÍA
1. Birger I. A. Cálculo de Resistencia
de Piezas de Máquinas. / I.A. Birger. [et.al.].—
Moscú: Editorial Mashinostroenie. 1986.2. Cherkasski, V.M .Bombas, Ventiladores y
Compresores/V M Cherkasski..—Moscú: Editorial
MIR Moscú, 1986. —372p3. Dobrovolski V. Elementos de Maquina/ V.
Dobrovolski…[et.al.].—Moscú: Editorial
MIR, 1970. —434p/4. Dossat, Roy J. Principios de
Refrigeración/Roy J Dossat…—México:
Editorial Continental, S.A, 1987—583p.5. Feodosiev V.I. Resistencia de Materiales/
V.I Feodosiev…— Moscú: Editorial MIR, 3ra
Edicion.1985. —583 p6. Iusilievich, G.B. Elementos de
Máquinas./G.B. Iusilievich.— Moscú:
Editorial Mashinostroenie, 1988. — 367 p.7. Ivanov, M.N. Elementos de
Máquinas./M.N. Ivanov. —Moscú: Editorial
Vischaya Schkola, 1991.–383 p.
Autor:
M.Sc. Ángel Rafael Martínez
León
Master en Ciencias. Jefe de Mantenimiento de la Planta
"Escambray";EPLE
Dr. Rafael Goytisolo Espinosa
Doctor en Ciencias Técnicas. Profesor Titular de
la Facultad de Mecánica de la UCf.
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |