Funciones de dos y más variables, dominio y rango, y curva de nivel
- Función de dos
variables - Funciones de varias
variables - Método
para hallar el Rango - Curvas
de nivel - Bibliografía
Función de
dos variables
Una función de
dos variables es
una regla de correspondencia que asigna a cada pareja de
números reales (x, y) un y sólo un
número real z.
El conjunto de parejas ordenadas para las cuales la
regla de correspondencia dá un número real se llama
dominio de la
función. El conjunto de valores
z que corresponden a los pares ordenados se llama
imagen o
contradominio.
Una función de dos variables se denota usualmente
con la notación
z = f (x,
y)
Las variables x, y se llaman variables
independientes, y z se llama variable
dependiente.
La gráfica de una función de dos variables
es el conjunto de puntos con coordenadas (x, y,
z) en donde (x, y) está en el
dominio de f y z = f (x,
y).
Este conjunto de puntos forma una superficie en el
espacio tridimensional.

En consecuencia, la grafica de una función
f de dos variables es una superficie que consta
de todos los puntos del espacio tridimensional cuyas coordenadas
cartesianas están determinadas por las ternas ordenadas de
números reales (x, y, z). Como el dominio de
f es un conjunto de puntos del plano x, y,
y puesto que cada par ordenado (x, y) del dominio de
f corresponde a solo un valor de
z, ninguna recta perpendicular al plano x,y puede
intersectar a la grafica de f en mas de un
punto.
Ejemplo ilustrativo 1
La función f del ejemplo 1 es el
conjunto de todos los pares ordenados de la forma (P, z) tales
que

z=v25- x2 -y2
Por tanto, la grafica de f
es la semiesfera en el plano x y por arriba de este cuyo
centro es el origen y tiene radio 5. Esta
semiesfera se muestra en la
figura 1.

Ejemplo 2: dibuje la grafica de la
función
Sol/: la grafica de f es la
superficie que tiene la ecuación z=x2 +y2 . La
traza de la superficie en el plano x,y se obtiene al
utilizar la ecuación z=0 simultáneamente con
la ecuación de la superficie. Al hacerlo resulta x2
+y2=0 la cual representa el origen. Las trazas en los planos
xz y yz se obtiene al emplear las ecuaciones
z=x2 +y2. Estos trazos son las parábolas z=
x2 y z= y2.

Funciones de
varias variables
El deseo de abordar problemas del
mundo real, nos conduce a tomar en cuenta que, en general,
cualquier situación o fenómeno requiere de
más de una variable para su precisa descripción. Por ejemplo, el volumen de un
cilindro depende del radio de la base y de su altura; la
posición de un móvil en un momento determinado
requiere para su exacta especiación, además del
tiempo, de las
tres coordenadas espaciales. Si adicionalmente se requiere la
velocidad a la
cual se desplaza, tendremos una función vectorial
f que a cada vector de cuatro componentes
(ubicación espacial y tiempo) le asigna la
velocidad
V del móvil en ese punto y en ese
instante:
f(x; y; z; t) =
v
Observamos entonces que de acuerdo con la
situación especifica que queramos describir, requerimos el
tipo de función adecuada. Según si el dominio D y
el rango R son subconjuntos de R; R2 o R3 las
funciones se
clasifican de la siguiente forma:
Función Nombre

En cada caso, donde aparece R3 lo podemos sustituir por
R2 y el nombre se conserva.
Las denominaciones escalar o vectorial se refieren a si
la imagen de la función es un
numero o es un vector.
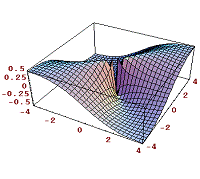
Ejemplo: la función g esta definida
por
g (x, y, z) = x2+y2-z
entonces el paraboloide circular z= x2+y2,
mostrado en la figura, es la superficie de nivel de g en
0. La superficie de nivel de g en el numero k tiene
la ecuación z + k = x2 + y2 , un paraboloide
circular cuyo vértice es el punto (0,0 –k) sobre el
eje z. en al figura muestra las superficies de nivel para
k igual a –4,-2, 0, 2 y 4
Página siguiente  |