Lógica proposicional en la inteligencia artificial (página 2)

2.4.1 SINTAXIS

Un buen lenguaje de
representación de conocimiento
debe de combinar las ventajas de los lenguajes naturales
(español, quechua, ingles, etc) y
lenguajes formales(C, pascal, lisp,
etc):

• Debe ser lo suficiente expresivo y conciso para que
  nos permita expresar de manera sucinta todo lo que hay que
  decir.
• Debe ser inequívoco (no ambiguo) e
  independiente del contexto para su interpretación.
• Debe ser eficiente en el sentido de que debe existir
  un procedimiento
  de inferencia que permita obtener nuevas inferencias a partir
  de oraciones en nuestro idioma.

2.4.2 SEMÁNTICA

• En lógica, el significado de
  una oración es aquello que se afirma del mundo, que el
  mundo sea de una forma.
• Una vez que mediante la semántica se interpreta una
  oración, ésta puede ser cierta o
  falsa.
• Una oración es cierta dentro de una
  interpretación determinada si el estado de
  asuntos que representa es cierta.
• El significado de una oración depende tanto de
  la oración como del contexto en que se
  produce.

III LÓGICA
PROPOSICIONAL

La lógica proposicional es una rama de la
lógica clásica que estudia las proposiciones o
sentencias lógicas, sus posibles evaluaciones de verdad y
en el caso ideal, su nivel absoluto de verdad.

La lógica proposicional se preocupa por la manera
de representar las cosas.

3.1 Proposición: se define una
proposición como un enunciado declarativo que puede ser
verdadero o falso, pero no ambos a la vez. Las proposiciones se
representan mediante variables
proposicionales simbolizadas mediante letras.

3.2 SINTAXIS DE LA LÓGICA DE
PROPOSICIONAL

Los patrones o expresiones de la lógica
proposicional se construyen a partir de un alfabeto que consta de
los siguientes símbolos:

• Las constantes lógicas Verdadero
  (
  ) y Falso (). También pueden ser V o
  F
• Los símbolos de variables tales como
  P y Q.
• Los conectivos lógicos Ù , Ú , Û ,
  Þ , y Ø
• Símbolos de puntuación:
  paréntesis ( ), corchetes [ ] y llaves { } para evitar
  ambigüedades

Todas las oraciones se forman combinando los
símbolos anteriores mediante ciertas
reglas.

• Las constantes lógicas Verdadero y
  Falso constituyen oraciones en sí
  mismas
• Las variables proposicionales P, Q, R,… son
  oraciones
• Encerrar entre paréntesis una oración
  produce también una oración, por
  ejemplo

(P Ù
Q).

Combinar oraciones con los conectadores
lógicos siguientes forma una oración

Oraciones: son Un conjunto de
palabras con sentido gramatical.

• La oración es la mínima unidad
  comunicacional, con significado completo.
• La oración en la lógica, es la unidad
  de análisis fundamental.

• Conjunción
  (Λ)
  (y). A la oración cuyo conector
  principal es Ù (y) se le
  llama conjunción, y a sus partes se les llama
  coyuntos.
• Disyunción (V) (o). A la oración
  cuyo conector principal es Ú
  (o) se le llama disyunción, y a sus partes se les llama
  disyuntos.
• Implicación (Þ ). Una oración como P
  Þ R se conoce como
  implicación (o condicional), su premisa o
  antecedente es P y su conclusión o
  consecuente es R. A las implicaciones también se
  les llama reglas o aseveraciones
  si-entonces.
• Premisas. Son los antecedentes de una
  implicación.
• Equivalencia.
• • Dos sentencias α
    y β son equivalentes
    lógicamente si es que son verdaderas con el mismo
    conjunto de hechos.
• Negación (Ø ) (no).
• • A una oración como Ø P se le llama
    negación de P. Ø es el único de los
    conectores que funcionan como una sola
    oración.

3.3 EJERCICIOS

FORMALIZAR LOS RAZONAMIENTOS:

1. " Si el resultado obtenido es superior al previsto en
   5 unidades, será debido a no haber realizado el proceso a la
   temperatura
   adecuada o a la existencia de errores en los cálculos
   finales."

Solución

p = Resultado obtenido menor al previsto en 5
unidades.

q = Haber realizado el proceso a la temperatura
adecuada.

r = Existencia de errores en los cálculos
finales.

q rp

2) " El análisis realizado, innecesario si nos
dejamos llevar por la precipitación, se torna necesario
si nos paramos a reflexionar sobre el mensaje que se pretende
transmitir."

solución

p = Análisis realizado es necesario.

q = Nos dejamos llevar por la
precipitación.

r = Nos paramos a reflexionar sobre el mensaje que se
pretende transmitir.

q pr p

3)" El
cáncer no logrará curarse a no ser que se
logre determinar su causa y se consiga encontrar
fármacos adecuados o bien para prevenirlo o para
curarlo."

solución

p = El cáncer logrará
curarse.

q = Se logra determinar su causa.

r = Se consigue encontrar fármacos adecuados
para prevenirlo.

s = Se consigue encontrar fármacos adecuados
para curarlo.

q r sp

3.4 SEMÁNTICA DE LA LÓGICA DEL
PROPOSICIONAL

• Una interpretación asocia cada variable
  proposicional con una proposición sobre el mundo.
  Porque las proposiciones son o verdades o falso, podemos
  también especificar una interpretación
  asignando los
  valores de verdad VERDAD y FALSO directamente a las
  variables proposicionales, sin importar qué
  proposición cada uno denota.
• Cada conector lógico es definido por una
  tabla de verdad
  Dado una interpretación de las variables
  proposicionales, nosotros podemos utilizar una tabla de
  verdad para calcular el valor de
  verdad de cualquier oración bajo esa
  interpretación

En términos generales, una
semántica permite atribuir un significado a las
expresiones del lenguaje simbólico considerado. En el caso
de un lenguaje de
programación como C, esta semántica es
procedural y consiste en describir el efecto que produce el
programa sobre
sus estructuras de
datos. Para
un lenguaje de representación, lo que interesa es capturar
una descripción del universo
modelado. La lógica permite hacer esto asignando un
valor de verdad a cada expresión del lenguaje.

La semántica de un lenguaje proposicional
depende

1. De la interpretación de los conectivos
   lógicos, que tienen el mismo significado en todos los
   dominios,
2. De los valores de
   verdad asignados a las variables proposicionales, distintos
   según la situación reflejada

3.5 TABLAS DE VERDAD

Se emplean en la lógica para determinar los
posibles valores de verdad de una expresión o
proposición. O si un esquema de inferencia, como
argumento, es formalmente válido mostrando que,
efectivamente, es una tautología.

La tabla de verdad de una sentencia es una tabla en la
que se presentan todas las posibles interpretaciones de las
variables proposicionales que constituyen la sentencia y el valor
de verdad de la sentencia para cada
interpretación.

Dado que en el cálculo
proposicional se opera sólo sobre dos valores de verdad,
para cualquier expresión existe un número finito de
valuaciones posibles que se pueden tabular.

La tabla de verdad de una expresión con
n variables proposicionales tiene 2n
filas

Semántica

• Negación Consiste en cambiar el valor
  de verdad de una variable proposicional.

• Disyunción: La sentencia
  será verdadera cuando una o ambas variables
  proposicionales sean verdaderas.

• Conjunción :La sentencia
  será verdadera sólo cuando ambas variables
  proposicionales sean verdaderas.

• Condicional

La sentencia será verdadera cuando se cumpla si
es válido p entonces lo es q.

• Bicondicional

La sentencia será verdadera cuando ambas
variables proposicionales sean iguales.

• Disyunción exclusiva

La sentencia será verdadera sólo cuando
sólo una de las dos variables proposicionales sea
verdadera, pero no las dos.

3.6 EQUIVALENCIA LÓGICA

Dos formulas A; B se dicen equivalentes (se
denota por B ó AB) si para toda
interpretación I, se cumple que Vi (A)= Vi(
B)

Teorema : A B si y sólo si la
fórmula A B es válida

A continuación se presenta una tabla con una
serie de equivalencias de uso común

1. Supresión de
Implicación:

1.1

2. Contraposición:

2.1

3. Supresión de Doble
Implicación:

3.1

4. Absorción:

5. Elemento neutro ( identidad)

2. A V A
3. A F A

5.3 A F F

5.4 A V V

6. Complementario-
Contradicción

6.1 A A F

6.2 AA V

F V

V F

7. Idempotencia

8. Commutativa

9. Asociativa

10. Distributiva

11. De Morgan

12. Doble Negación

3.7 VALIDEZ E INFERENCIA

Los términos "razonamiento" e "inferencia" son
utilizados para referirse a cualquier proceso mediante el que se
obtienen conclusiones.

Las tablas de verdad sirven no solo para definir los
conectores, sino también para probar la validez de las
oraciones. Si se desea considerar una oración, se
construye una tabla de verdad con una hilera por cada una de las
posibles combinaciones de valores de verdad correspondientes a
los signos
proposititos de la oración. Se calcula el valor de verdad
de toda la oración, en cada una de las hileras. Si la
oración es verdadera en cada una de las hileras. La
oración es valida.

Las tablas nos manifiestan los valores de verdad de
cualquier proposición, así como el análisis
de los mismos, encontrándonos con los siguientes
casos:

• Tautología o validez:

Se entiende por proposición tautológica,
o tautología, aquella proposición que en todos
los casos posibles de su tabla de verdad su valor siempre es
V.

• Contradicción:

Se entiende por proposición contradictoria, o
contradicción, aquella proposición que en todos
los casos posibles de su tabla de verdad su valor siempre es
F

• Contingencia (verdad
  indeterminada)

Se entiende por verdad contingente, o verdad de hecho,
aquella proposición que puede ser verdadera o falsa, o
no se tiene suficiente información para llegar a una
conclusión

• Satisfabilidad.

Si en la tabla de verdad se obtiene al menos una
VERDAD

3.8 EJERCICIOS

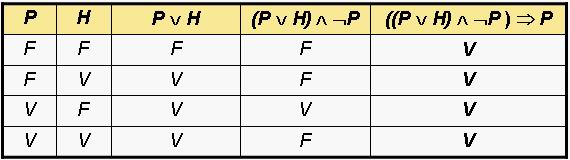
1. ((P Ú H)
   Ù
   Ø P )
   Þ P

   Solución

   

   Respuesta: sí es
   valida

2. Determinar La Validez De La Siguiente oración
   compleja
   • Si no llueve salgo al campo. Si salgo al campo
     respiro. Por tanto, respiro si y sólo si no
     llueve."

   Respuesta:

   NO es válido, puedo salir al campo,
   lloviendo y respirar. Luego no se deduce que respire si y
   solo si no llueve.

   • Si ha nevado será difícil
     conducir. Si no es fácil conducir llegaré
     tarde si no salgo temprano. Ha nevado. Luego
     saldré temprano.

   Respuesta

   El razonamiento NO es válido porque puede
   darse el caso de NO salir temprano y llegar tarde habiendo
   nevado y siendo difícil conducir.
   Cumpliéndose todas las premisas.

   3.9 REGLAS DE INFERENCIA

   • Existen ciertos patrones de inferencia que se
   presentan una y otra vez, lo que permite establecer de una
   vez por todas su confiabilidad.

   • La regla permite evitar pasar por las tablas
   de verdad.

   1. A partir de una implicación y la premisa
      de la implicación, se puede inferir la

      conclusión.

      

   2. Modus ponens o
      implicación-Eliminación:

      A partir de una conjunción se puede
      inferir cuales son los coyuntos(elementos)

      

   3. Y- Eliminación:
      (eliminación de ^ )

      A partir de una lista de oraciones es posible
      inferir su conjunción

      

   4. Y- Introducción (Introducción del
      ^)

      A partir de una oración es posible
      inferir su disyunción con todo lo
      demás.

      

   5. O– Introducción
      (Introducción del Ú )

      A partir de una oración doblemente
      negada, es posible inferir una oración
      positiva

      

   6. Eliminación de la doble
      negación:

      A partir de una disyunción, si uno de los
      disyuntos es falso, entonces se puede inferir que el otro
      es verdadero.

      

   7. Resolución unitaria
   8. resolución:

   Es la mas difícil. Puesto que B no puede
   ser al mismo tiempo
   verdadera ni falsa, uno de los otros disyuntos debe ser en
   una de las premisas. O también, que la
   implicación es transitiva.

   

   3.10 EJERCICIOS

   • Utilice la tabla de verdad para determinar para
     demostrar que la siguiente oración es valida y que
     por lo tanto la equivalencia es correcta

   P^ (q rp ^ q) ( p^
   r)]

   p	q	r	P ^ (q r) p ^ q) ( p^ r)
   V	V	V	V	V	V	V	V	F	F	V	V
   V	V	F	V	F	F	V	V	F	F	F	F
   V	F	V	V	V	V	V	V	V	V	V	V
   V	F	F	V	V	V	V	V	V	V	V	F
   F	V	V	F	F	V	V	F	F	F	F	F
   F	V	F	F	F	F	V	F	F	F	F	F
   F	F	V	F	F	V	V	F	F	V	F	F
   F	F	F	F	F	V	V	F	F	V	F	F

   

   TAUTOLOGIA

   Por tanto: P^ (q r) [p ^
   q) ( p ^ r)], Es válida y
   equivalente

   • Haciendo uso de la lógica equivalente
     simplificar las siguiente
     proposición

    

   • ( P ^ q)

   ( P ^ q )

   P ^ ( q q)
   …………………………..R.
   Distributiva(10.2)

   P ^ ( V )
   …………………….R. Complementaria
   (6.2)

   P ……………………………..R. Identidad
   (5.1)

   • Haciendo uso de las reglas de inferencia
     Demostrar que :

   p q q p

   1. p q Premisa

   2. q Regla. Eliminación de ^
   (1)

   3. p Regla. Eliminación de ^
   (1)

   4. q p Regla. Introducción del
   2,3)

   BIBLIOGRAFÍA

   • 
     http://ftp.gnuab.org/pub/eresvago/ficheros/apuntes/segundo/lc/logica_proposicional.pdf
   • 
     http://platon.escet.urjc.es/grupo/docencia/LC/introduccion.pdf
   • STUART RUSSELL, PETER NORVING. Inteligencia
     Artificial un enfoque moderno.

   PrenticeHall, México, 1998

    

   Kelly Camacho1

   Sheyla Juárez1

   Silvia Vilchez1

   1Escuela Profesional de
   Computación e informática, Universidad Nacional Pedro Ruiz Gallo,
   Lambayeque – Perú

3. Compruébese si los siguientes razonamientos
   son correctos o no: