Indice
1.
Teorema de pitagoras
3.
Observaciones.
4. Lema (1-D). Conformación de las
ternas originales
fraccionarias.
5. Clasificación de las ternas
originales.
6. Las ternas
primarias..
7. Secuencia de las
raíces.
8. Los triángulos rectángulos
isósceles.
9. Triángulos con ángulos
complementarios de 300 y
600
10.
Interpretación
geométrica.
11. Lugar
geométrico.
12. Funciones
trigonométricas.
1. Teorema de pitagoras
El conocimiento
del teorema de Pitágoras es milenario y no obstante que ha
sido demostrado en muchas formas diferentes y de que
aparentemente ya se conoce todo con respecto a este teorema,
muchas propiedades sorprendentes de la ecuación
Pitagórica han permanecido ocultas.
Damos gracias a Dios por concedernos la percepción
de algunas de esas maravillas.
En esta lectura se
propone un método
para clasificar las ternas pitagóricas, este método
constituye la verdadera y completa solución de la
ecuación pitagórica y también les confiere a
dichas ternas su estado normal
en armonía con las leyes
naturales.
Si 
son
enteros y 
satisfacen 
,
entonces existen infinitas ternas pitagóricas con
diferente configuración, como se muestra a
continuación:
Actualmente, bajo el criterio vigente, para asignar a
una terna la categoría de primitiva, es suficiente que la
terna satisfaga las siguientes dos condiciones:
satisfacen, entonces existen infinitas ternas
Pitagóricas con diferente configuración, como
mostramos enseguida:
La nueva solución está basada en el origen
numérico de la ecuación y corrige la antigua y
errónea clasificación para las llamadas "ternas
pitagóricas primitivas", También unifica bajo un
criterio generalizado las leyes que rigen
sus diferentes parámetros de
conformación.
Seguidamente mostramos varios conjuntos de
ternas Pitagóricas con diferentes valores de
que además
de las condiciones expuestas anteriormente también
satisfacen que.
Para 
:
Para 
{8, 15, 17}, {12, 35, 37}, {16, 63, 65},
{20, 99, 101}, {24, 143, 145}
Para 
:
Para 
Podemos apreciar que la secuencia de las diferencias, es
decir, la diferencia entre las magnitudes correspondientes a la
hipotenusa y el cateto mayor es: 
A continuación determinaremos cual es el
patrón general para la conformación de la
ecuación:
Si 
entonces 
puede ser un entero par o impar.
es impar
sí y solo sí 
es decir, el cuadrado de cualquier número
impar.
es par si
y solo si 
es
decir, que partiendo de la diferencia entre cada dos de los
números siguientes se incrementa sucesivamente en 4
unidades, enseguida se muestra la
secuencia ascendente del incremento de la diferencia:
La siguiente es la secuencia de conformación
de:
La solución ancestral para la
ecuación 
,
(1.1)
El texto en
negrilla fue traducido literalmente del libro "13
lectures on Fermat's last theorem" por Paulo Ribenboim. AMS
classification (1980): 10-03, 12-03, 12Axx
Sí son enteros, diferentes de cero, que satisfacen
(1.1)
Considerando los valores
absolutos 
, estos
números son las longitudes de los lados de un
triángulo rectángulo
Para determinar todas las soluciones
enteras no triviales de (1.1), basta determinar las llamadas
ternas pitagóricas primitivas
,
, 
.
El siguiente teorema da una descripción completa
de las denominadas ternas primitivas:
(1A) Si 
son enteros diferentes de cero y de paridad
diferente,
Si se cumple que: 
Entonces la terna 
es denominada Pitagórica primitiva.
El siguiente texto, entre [
], fue traducido del libro de Paulo
Ribenboim "13 lectures on Fermat's last theorem". AMS
clasificación (1980): 10-03, 12-03, 12Axx.
[ Las menores ternas primitivas ordenadas de
acuerdo a incrementos en los valores de
z, son las siguientes:
Fermat demostró el siguiente teorema: n > 0 es
la suma de los cuadrados de dos números enteros Sí
y solo si cada factor primo p de n, tales que p º 3 (mod.
4), aparece como una potencia par en
la descomposición de n en factores primos.
Para encontrar el número de representaciones de
la suma de dos cuadrados. Si r(n) es el número de parejas
de enteros (a, b) de manera que n = 
. Por ejemplo, r (1) = 4 y r (5) = 8. La
determinación de r (n) en factores primos fue elaborada
independientemente por Gauss y Jacobi:
,
donde:
| 1 £ d, d ½ n, 
| 1 £ d, d ½ n, 
]
2. La verdadera y
completa solución
Demostraremos, que una terna Pitagórica es
original, si y solo si satisface los parámetros que
posteriormente serán definidos, tales parámetros
determinan que las ternas originales se configuran exclusivamente
en la forma: 
, de
manera que
.
Denomino original a toda terna Pitagórica cuya
configuración corresponde al modelo
anterior.
A continuación muestro la forma en que represento
las diferentes clases de ternas
Primitivas, de acuerdo con el método
tradicional
Originales, enteras o fraccionarias.
Primarias.
Bajo el criterio vigente x es par e y es impar, bajo el
nuevo X es impar, mientras que Y es par.
Cuando n es una fracción, la llamo
fracción generatriz y la represento como 
.
Se considera, sin pérdida de generalidad, que el
lado menor de cualquier triángulo rectángulo, es
siempre adyacente al ángulo denominado a , lo cual implica
que cosa es siempre menor que sena ..
Los conjuntos
involucrados en las demostraciones se simbolizan de la forma
siguiente:
Z + = Enteros positivos.
Q = Fracciones racionales positivas.
F = Fracciones irracionales positivas.
Se restringe el nuevo criterio, sin pérdida de
generalidad, al primer cuadrante, es decir a ángulos
comprendidos entre cero y 
, por lo tanto, a enteros positivos y fracciones
positivas racionales o irracionales.
Teorema (1-B). Para cada 
existen tres números enteros 
, de tal manera, que
satisfacen las siguientes condiciones:
E-4
E-5
E-6
E-7
E-8
Lema (1-B).-Sí 
y sí 
entonces 
es equivalente a un
binomio cuadrado perfecto, en la forma siguiente:
como 
,
siendo 
, esto
implica que 
,
reemplazando
por
en 
resulta que 
.
El siguiente es un resumen del proceso
empleado para encontrar la sucesión pertinente:
Las siguientes ternas 
, en las cuales , satisfacen 
{(3, 4, 5), (5, 12, 13), (7, 24,
25), (9, 40, 41), (11, 60, 61), (13, 84,
85), (15 112, 113),.., }
Los números resaltados: { 4, 12, 24, 40, 60, 84,
112,.., ¥ , son las magnitudes correspondientes al lado Y
para todo triángulo cuyos lados satisfacen 
En la siguiente tabla, sin tomar en cuenta el factor
, el primer
término de cada binomio, dentro del paréntesis
subrayado en la columna a la izquierda, es igual a la suma de los
dos términos contenidos dentro del paréntesis
anterior, también subrayado, El segundo término del
mismo binomio, es igual al segundo término del binomio
precedente, incrementado en 1.
También, cada binomio sobre la misma primera
columna, es equivalente a la adición de los enteros
sucesivos expresados dentro del paréntesis inmediato a la
derecha.
4 = 4 x 1 = 22.(0+1) =
22.(0+1)—————-n = 1 Þ Y = 2n.(n+1) = 2
x 1.(1 + 1)
12 = 4 x 3 = 22.(1+2) =
22.(1+2)—————-n = 2 Þ Y = 2n.(n+1) = 2
x 2.(2 + 1)
24 = 4 x 6 = 22.(3+3) =
22.(1+2+3)————-n = 3 Þ Y = 2n.(n+1) = 2
x 3.(3 + 1)
40 = 4 x 10 = 22.(6+4)
= 22.(1+2+3+4)———-n = 4 Þ Y = 2n.(n+1) = 2
x 4.(4 + 1)
Por lo tanto, para cada 
-existe una terna , de tal forma, que satisface
en la cual Y es
equivalente a multiplicado por la suma de los enteros consecutivos
contenidos entre 1 y n.
Es conocido que la suma de una sucesión de
enteros positivos entre 1 y n, es equivalente a la mitad del
producto de n
por su sucesor, como se muestra a
continuación:
Ejemplo: 
Lema (2-B). Por lo tanto, 
Sí X es un número impar mayor que 1 que
corresponde a la forma 
, aplicando entonces para hallar Z un proceso
similar al usado para encontrar Y, resulta:
Para todo 
se cumple que
De igual manera, las anteriores expresiones satisfacen
(E-4), (E-5), (E-6), (E-7), (E-8), como sigue:
Para que una terna de números enteros, 
sea original, los tres
términos tienen que ser una función de la
sumatoria: 
.
Para que cualquier impar 
, sea primo, necesariamente
Representaré la función correspondiente a
la sumatoria de fracciones así:
Teorema (1-D). Para cada fracción 
, racional o
irracional, 
, existen tres fracciones racionales o irracionales,
, 
, de tal forma, que satisfacen las siguientes
condiciones:
4. Lema (1-D).
Conformación de las ternas originales
fraccionarias.
Las ternas: 
= (45, 28, 53), (55, 48, 73), (95, 168, 193),
satisfacen 
Dividiendo los tres términos de cada una de estas
ternas por 
, que
es común para las tres, obtenemos respectivamente las
siguientes ternas formadas por tres fracciones a las cuales
representaremos en forma general como , y que satisfacen
,
Los valores
correspondientes a Y, para cada una de estas ternas
son: 28/ 25, 48/ 25, 168/ 25
A continuación determinaré el
patrón que rige su conformación.
Emplearé indistintamente
para representar la función
,
,
están conformadas de acuerdo a un
mismo patrón, así: 
Como 
e
.
Si q es impar y como 
, esto implica que:
Representando por l y h , respectivamente, los
numeradores del primero 
y del último término 
de la sumatoria, esta se
reduce a la forma siguiente:
Como 
,
entonces Sí q es impar, 
es par, de manera que, 2 aparece como factor en la
descomposición de 
en factores primos, por lo tanto 
es divisible por 2.
Esto implica que tanto l como los demás numeradores de los
términos de la sumatoria se reducen a enteros.
Sí q es par implica que es impar y por lo tanto no divisible por
2, entonces l y los demás numeradores de los
diferentes términos de la sumatoria son fracciones
irreducibles a enteros
Las siguientes son las propiedades de la sumatoria
:
Común denominador = 
Numerador del primer término =
Numerador del último término =
Numero de términos = p.
En el ejemplo siguiente el denominador q, de la
fracción generatriz, es par.
Por lo tanto:
Para la conformación de las ternas
pitagóricas fraccionarias irracionales rigen los mismos
parámetros que para la de las fraccionarias
racionales:
Los siguientes son los tres casos posibles:
1- p es racional y q irracional
2- p es irracional y q racional
3- p y q son irracionales.
Para determinar el desarrollo de
la sumatoria correspondiente al primer caso, cuando p es racional
y q irracional, basta aplicar el método empleado cuando p
y q son enteros, es decir 
es racional.
Por ejemplo: 
El número de términos de la sumatoria es
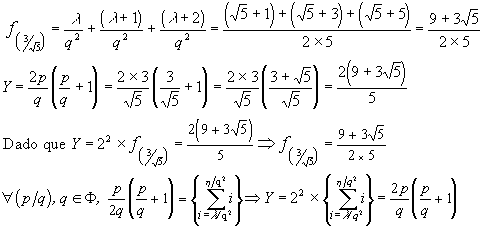
Para determinar el número de términos, que
obviamente tiene que ser entero, si p es irracional y q racional,
es necesario racionalizar p,. de esta manera el caso se
reduce al anterior.
Por ejemplo: 
, racionalizando p, resulta que 
,
entonces 
Despejando Y, a partir de la fracción
inicial
,
sin racionalizar 
:
,
Dado que 
, entonces 
Por lo tanto, 
Para el desarrollo de
la sumatoria en el tercer caso, es decir cuando p y q son
irracionales, también resulta evidente la necesidad de
racionalizar p
El número de términos es: 
Despejando Y a partir de la fracción inicial
, sin racionalizar
:
, dado que 
entonces 
Por lo tanto:
Para el mismo tercer caso, si (p, q) son irracionales
propios, se procede en general de la siguiente manera:
(Denomino irracionales propios a los irracionales cuya
racionalización es imposible).
(Selecciono 2 como factor auxiliar en el numerador y
denominador de la fracción generatriz, ya que así
se reducen a este número los términos de la
sumatoria).
Cuando 
,
como en el caso siguiente: 
Despejando Y a partir de la fracción inicial
, 
Por lo tanto, para toda fracción p/ q, (p,
q) irracionales propios, 
Como 
,
correspondiendo Y a una terna 
que satisface las 8 condiciones establecidas en el
teorema (1-D), aplicando entonces para X y Z,
resulta:
*En referencia a la
representación de enteros positivos impares como la suma
de dos cuadrados, las nuevas expresiones anteriormente expuestas,
no son válidas únicamente para enteros como son los
hallazgos en esta materia de
Fermat, Gauss y Jacobi; sino que también aplican para
fracciones tanto racionales como irracionales.
Corolario (1-B). Dado que 
, esto implica, que el cuadrado de todo
número impar mayor que 1, es igual a la suma de dos
números enteros consecutivos, así:
Corolario (1-C). Dado que 
, entonces, 
es igual a un entero par y como 
, resulta que el cuadrado
de todo número impar es igual a la suma de dos fracciones
racionales consecutivas.
(Consideramos que dos fracciones son consecutivas cuando
su diferencia es 1).
Ejemplos:
5. Clasificación de
las ternas originales.
1.- Enteras———-Las que están formadas por
tres enteros.
2.- Fraccionarías—Dos o los tres
términos son fracciones.
3.- Irracionales—–Uno o mas términos son
irracionales.
Las ternas primarias son las formadas por enteros
, que son
primos relativos, es decir 
, y satisfacen 
, pero 
y tampoco cumplen el resto de condiciones necesarias para
ser originales.
Dividiendo los tres términos, , de una terna primaria,
por 
, obtenemos la
correspondiente terna original en la cual la hipotenusa, del
correspondiente triángulo, es igual al cateto mayor mas 1,
por este medio podemos reducir cualquier terna primaria a su
estado
original.
Dividiendo por e
igualando los resultados a 
respectivamente, obtenemos:
Entonces 
.
Por ejemplo: la terna primaria, 
corresponden. 
, lo cual determina que la terna
, sea
original. Entonces 
, donde
Para obtener cada terna primaria 
basta amplificar la correspondiente terna
original fraccionaria. Por cada reemplazo de n por una diferente
fracción 
,
obtendremos una diferente terna original fraccionaria.
Las fracciones generatrices 
, originan las menores ternas
fraccionarias originales, ordenadas de acuerdo a incrementos de
X, (X entero y par), así:
Las siguientes son las ternas primarias que corresponden
respectivamente a las ternas originales del conjunto anterior,
tales ternas cumplen 
, son primos relativos, pero no satisfacen el resto de
condiciones necesarias para ser originales.
Resulta el siguiente conjunto de ternas que satisfacen
los parámetros necesarios para ser originales:
,..,
Intercalando en forma ordenada, de acuerdo a los valores
pares e impares de X, resulta:
A continuación probaremos el cumplimiento de la
terna 
con
relación a los parámetros determinantes del estado
original.:
Reduciendo a un común denominador, en este caso
2, al cancelar dicho denominador resultan las siguientes ternas
primarias conformadas por tres enteros, 
,que son primos relativos, y satisfacen
que 
, pero no
así, las restantes condiciones necesarias para ser
originales.
Ejemplos
Las ternas 
son solamente primarias.
Dado que 
, esto determina que 
es un punto de convergencia, lo cual implica que
, es decir,
sí 
entonces X tiene que ser menor que Y. Esto es válido
para las ternas fraccionarias originales y por ende para las
primarias.
Recíprocamente, Sí 
por lo tanto, las raíces
originales 
,
constituyen parejas ordenadas y sus respectivos valores no son
permutables con relación al cumplimiento de las
condiciones determinantes de la originalidad.
Permutando los valores correspondientes de 
, en una terna primaria,
donde 
Por ejemplo,
la terna 
entonces
la terna se convierte en 
, y por lo tanto 
Sí el valor de q
correspondiente a una fracción generatriz p/ q, es 2, esto
determina una clase de ternas originales en las cuales X es un
entero par y tanto Y como Z son fracciones cuyos numeradores son
impares y sus denominadores son iguales a 2.
Sí 
, dado que, 
esto determina que p es impar y por lo tanto, 
es par.
, Si p es impar 
también es
impar,
, Sí p es impar 
también es
impar.
8. Los triángulos
rectángulos isósceles.
La terna 
, asociada usualmente con estos triángulos no
satisface las condiciones de originalidad. Considerando, que los
catetos tienen que ser iguales entre sí, entonces
Por (E-7),
Por lo
tanto,
Como 
,
despejando n, resulta que la fracción generatriz es:
.
Es interesante despejar la misma terna original a partir
de 
, como
sigue:
La terna 
satisface las condiciones para ser
original.
9. Triángulos
con ángulos complementarios de 300 y
600
Dado que 
representan los lados de tales triángulos, reducidos
a su mínima expresión, y como (
, La terna 
, satisface las ecuaciones
comprendidas entre (E- 1) y (E- 8).
Reemplazando 
las menores ternas originales enteras, ordenadas de acuerdo
a incrementos en los valores impares de X, son las
siguientes:
El siguiente conjunto corresponde a las menores ternas
primitivas, ordenadas de acuerdo al criterio ancestral, es decir
a incrementos del valor de z
:
A continuación mostramos las mismas ternas,
ordenadas de acuerdo a incrementos de X:
Las hipotenusas correspondientes a los triángulos
de lados (3, 4, 5), (5, 12, 13), (7, 24, 25). son respectivamente
iguales al cateto mayor del triángulo, incrementado en
1.
Las hipotenusas correspondientes a los triángulos
de lados
,
tienen una configuración, diferente a las
anteriores, así:
respectivamente. A partir de esto sacamos como
conclusión, que las ternas del primer arreglo son
originales y las ternas del segundo son primarias.
Seguidamente reduciremos las ternas primarias
a su
correspondiente estado original,
Dividiendo:
,resultan respectivamente 
Como 
, despejando n, resulta que 
, aplicando (E-1), (E-2), (E-3),
comprobamos que 
son respectivamente
, esta
terna es original, la otra, 
, solamente es primaria.
Dividiendo 
, es decir por 2, resultan:
Como 
,
despejando n, resulta que 
, aplicando (E-1), (E-2), (E-3), comprobamos que
son
respectivamente 
constituyendo la terna original correspondiente a la
primaria 
.
es la
terna original correspondiente a la primaria 
. La original
correspondiente a la primaria 
, es 
. El hecho de tener diferentes ternas originales, determina
que los valores de 
en una terna primaria no son , de acuerdo a lo expuesto con
anterioridad, no son permutables y constituyen parejas
ordenadas.
10. Interpretación
geométrica.
Las ecuaciones
(E-1), (E-2) ), (E-3), son las ecuaciones
paramétricas de un plano que corta los ejes de coordenadas
, de tal
manera que las distancias entre los puntos de intercepción
con los ejes y el origen, corresponden siempre a los lados de un
triángulo rectángulo, el plano determinado por
dichas intersecciones está representado por la siguiente
ecuación, en forma simétrica
Donde 
son
las longitudes determinadas sobre los ejes por las intersecciones
del plano. d .
Para nuestro caso, las magnitudes de los segmentos son
respectivamente:
Por lo tanto la ecuación es la siguiente :
Y en forma general: 
La ecuación d es el lugar geométrico de
las rectas que se desplazan de tal manera, que las
magnitudes de las distancias entre sus puntos de
intercepción con los ejes de coordenadas y el origen
satisfacen el conjunto de ecuaciones de (E-1) a (E-8).
La longitud entre el origen y los puntos donde el plano
d se intercepta con el eje Z, es equivalente a la longitud de la
traza del mismo plano sobre el plano XY, es decir:
Las expresiones anteriores simbolizan la hipotenusa de
todos los triángulos rectángulos, cuyos otros lados
son respectivamente iguales a la raíz cuadrada de las
cantidades subradicales.
12. Funciones
trigonométricas.
Para la existencia de ternas originales irracionales, es
necesario que cos2a y sen2a sean fracciones
racionales que corresponden a los cuadrados de las respectivas
funciones
trigonométricas, determinadas por la apropiada
razón entre los lados , de cualquier triángulo rectángulo,
cuyas magnitudes son enteros o también fracciones tanto
racionales como irracionales.
La razón apropiada entre las magnitudesÎ [Z +
(QF )] representa las
funciones trigonométricas para los ángulos de cada
triángulo determinado por las intercepciones entre el
plano d y los ejes de coordenadas.
Las siguientes expresiones representan respectivamente
las fracciones correspondientes a las funciones sena , cosa ,
tang a , para todo ángulo a , (0 < a < p / 2 ), de
manera que sen2a , cos2a , tan2a
, son fracciones racionales. Dichas expresiones constituyen
fórmulas cuyo ámbito es infinito.
Bajo el mismo contexto obtendremos fórmulas
infinitas para el resto de funciones.
Y así sucesivamente para el resto de
funciones.
Sí 
, entonces 
Por lo tanto, las fórmulas en función de las
ecuaciones (E-1), (E-2), (E-3), desarrolladas anteriormente para
la solución de las ternas enteras, se reducen
así:
Resumen:
El trabajo es
un estudio sobre la conformación de las ternas
pitagóricas, en el mismo se determina el origen
numérico del teorema de Pitágoras y se introduce
una nueva clasificación para la conformación de las
respectivas ternas también se determina la
conformación de ternas fraccionarias.
Se cree que se conoce todo sobre dicho teorema, pero en esta
investigación se revelan muchas propiedades
sorprendentes que han permanecido ocultas durante milenios.
También se puede encontrar un análisis sobre la interpretación
geométrica y el lugar geométrico de la
ecuación pitagórica lo mismo que formulas infinitas
para las funciones trigonométricas.
Por su total originalidad no incluye bibliografía.
Trabajo enviado por:
Rubén Moré Argel
Ingeniero Industrial, edad 60 años nacido en Cartagena
Colombia
especializado en procesos de
polimerización.
Dirección: A. A # 8586
Cartagena, Colombia. Sur
América
rubenmore[arroba]hotmail.com