Partes: 1, 2

¿CÓMO INTERPRETAR UN DIAGRAMA DE CAUSA-EFECTO?

El diagrama Causa-Efecto es un vehículo para ordenar, de forma muy concentrada, todas las causas que supuestamente pueden contribuir a un determinado efecto. Nos Permite, por tanto, lograr un conocimiento común de un problema complejo, sin ser nunca sustitutivo de los datos. Es importante ser conscientes de que los diagramas de causa-efecto presentan y organizan teorías. Sólo cuando estas teorías son contrastadas con datos podemos probar las causas de los fenómenos observables.

Errores comunes son construir el diagrama antes de analizar globalmente los síntomas, limitar las teorías propuestas enmascarando involuntariamente la causa raíz, o cometer errores tanto en la relación causal como en el orden de las teorías, suponiendo un gasto de tiempo importante.

¿CÓMO ELABORAR UN DIAGRAMA DE CAUSA-EFECTO?

1. Definir claramente el efecto o síntoma cuyas causas han de identificarse.
2. Encuadrar el efecto a la derecha y dibujar una línea gruesa central apuntándole.
3. Usar Brainstorming o un enfoque racional para identificar las posibles causas.
4. Distribuir y unir las causas principales a la recta central mediante líneas de 70º.
5. Añadir subcausas a las causas principales a lo largo de las líneas inclinadas.
6. Descender de nivel hasta llegar a las causas raíz (fuente original del problema).
7. Comprobar la validez lógica de la cadena causal.
8. Comprobación de integridad: ramas principales con, ostensiblemente, más o menos causas que las demás o con menor detalle.

A continuación veremos como el valor de una característica de calidad depende de una combinación de variables y factores que condicionan el proceso productivo (entre otros procesos).

El ejemplo se basa en el proceso de fabricación de mayonesa, para así explicar los Diagramas de Causa-Efecto:

La variabilidad de las características de calidad es un efecto observado que tiene múltiples causas. Cuando ocurre algún problema con la calidad del producto, se debe investigar a fin de identificar las causas del mismo. Para hacer un Diagrama de Causa-Efecto se siguen los siguientes pasos:

Se decide cuál va a ser la característica de calidad que se va a analizar. Por ejemplo, en el caso de la mayonesa podría ser el peso del frasco lleno, la densidad del producto, el porcentaje de aceite, etc.

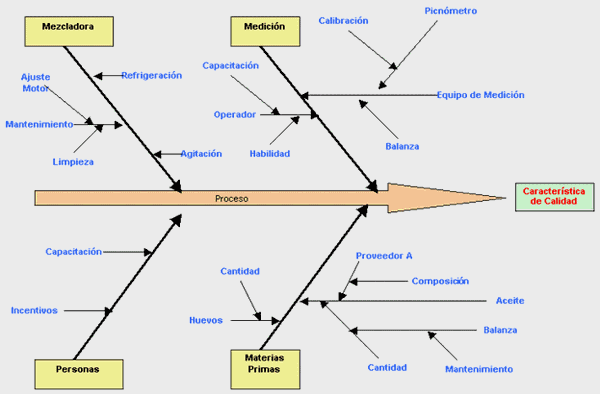
Se traza una flecha gruesa que representa el proceso y a la derecha se escribe la característica de calidad:

 

Se indican los factores causales más importantes y generales que puedan generar la fluctuación de la característica de calidad, trazando flechas secundarias hacia la principal. Por ejemplo: Materias Primas, Equipos, Operarios, Método de Medición, etc.:

Se incorporan en cada rama factores más detallados que se puedan considerar causas de fluctuación. Para hacer esto, se pueden formular estas preguntas:

• ¿Por qué hay fluctuación o dispersión en los valores de la característica de calidad? Por la fluctuación de las Materias Primas. Se anota Materias Primas como una de las ramas principales.
• ¿Qué Materias Primas producen fluctuación o dispersión en los valores de la característica de calidad? Aceite, Huevos, sal, otros condimentos. Se agrega Aceite como rama menor de la rama principal Materias Primas.
• ¿Por qué hay fluctuación o dispersión en el aceite? Por la fluctuación de la cantidad agregada a la mezcla. Agregamos a Aceite la rama más pequeña Cantidad.
• ¿Por qué hay variación en la cantidad agregada de aceite? Por funcionamiento irregular de la balanza. Se registra la rama Balanza.
• ¿Por qué la balanza funciona en forma irregular? Por que necesita mantenimiento. En la rama Balanza colocamos la rama Mantenimiento.

Así se sigue ampliando el Diagrama de Causa-Efecto hasta que contenga todas las causas posibles de dispersión.

Finalmente se verifica que todos los factores que puedan causar dispersión hayan sido incorporados al diagrama. Las relaciones Causa-Efecto deben quedar claramente establecidas y en ese caso, el diagrama está terminado.

Un diagrama de Causa-Efecto es de por si educativo, sirve para que la gente conozca con profundidad el proceso con que trabaja, visualizando con claridad las relaciones entre los Efectos y sus Causas.

Sirve también para guiar las discusiones, al exponer con claridad los orígenes de un problema de calidad. Y permite encontrar más rápidamente las causas asignables cuando el proceso se aparta de su funcionamiento habitual.

DIAGRAMA DE PARETO

El Diagrama de Pareto es una gráfica en donde se organizan diversas clasificaciones de datos por orden descendente, de izquierda a derecha por medio de barras sencillas después de haber reunido los datos para calificar las causas. De modo que se pueda asignar un orden de prioridades.

El nombre de Pareto fue dado por el Dr. Joseph Juran en honor del economista italiano Vilfredo Pareto (1848-1923) quien realizó un estudio sobre la distribución de la riqueza, en el cual descubrió que la minoría de la población poseía la mayor parte de la riqueza y la mayoría de la población poseía la menor parte de la riqueza. Con esto estableció la llamada "Ley de Pareto" según la cual la desigualdad económica es inevitable en cualquier sociedad.

Vilfredo Pareto 1848-1923

El Dr. Juran aplicó este concepto a la calidad, obteniéndose lo que hoy se conoce como la regla 80/20.

Según este concepto, si se tiene un problema con muchas causas, podemos decir que el 20% de las causas resuelven el 80% del problema y el 80% de las causas solo resuelven el 20% del problema.

Por lo tanto, el Análisis de Pareto es una técnica que separa los "pocos vitales" de los "muchos triviales". Una gráfica de Pareto es utilizada para separar gráficamente los aspectos significativos de un problema desde los triviales de manera que un equipo sepa dónde dirigir sus esfuerzos para mejorar. Reducir los problemas más significativos (las barras más largas en una Gráfica Pareto) servirá más para una mejora general que reducir los más pequeños. Con frecuencia, un aspecto tendrá el 80% de los problemas. En el resto de los casos, entre 2 y 3 aspectos serán responsables por el 80% de los problemas.

Usando el Diagrama de Pareto se pueden detectar los problemas que tienen más relevancia mediante la aplicación del principio de Pareto (pocos vitales, muchos triviales) que dice que hay muchos problemas sin importancia frente a solo unos graves.

La gráfica es útil al permitir identificar visualmente en una sola revisión tales minorías de características vitales a las que es importante prestar atención y de esta manera utilizar todos los recursos necesarios para llevar acabo una acción correctiva sin malgastar esfuerzos.

En relación con los estilos gerenciales de Resolución de Problemas y Toma de Decisiones, se puede ver como la utilización de esta herramienta puede resultar una alternativa excelente para un gerente de estilo Bombero, quien constantemente a la hora de resolver problemas sólo "apaga incendios", es decir, pone todo su esfuerzo en los "muchos triviales".

Algunos ejemplos de tales minorías vitales serían:

• La minoría de devoluciones que representa la mayoría de quejas de la clientela.
• La minoría de compradores que representen la mayoría de las ventas.
•     La minoría de productos, procesos, o características de la calidad causantes del grueso de desperdicio o de los costos de reproceso.
• La minoría de vendedores que esta vinculada a la mayoría de partes impugnadas.
• La minoría de problemas causantes del grueso del retraso de un proceso.
• La minoría de productos ó servicios que representan la mayoría de las ganancias obtenidas.
• La minoría de elementos que representan al grueso del costo de un inventario.

Se recomienda su uso:

• Para identificar oportunidades para mejorar
• Para identificar un producto o servicio para el análisis para mejorar la calidad.
• Cuando existe la necesidad de llamar la atención a los problema o causas de una forma sistemática.
• Para analizar las diferentes agrupaciones de datos.
• Al buscar las causas principales de los problemas y establecer la prioridad de las soluciones.
• Para evaluar los resultados de los cambos efectuados a un proceso (antes y después).
• Cuando los datos puedan clasificarse en categorías.
• Cuando el rango de cada categoría es importante.

¿CUÁNDO SE UTILIZA?

• Al identificar un producto o servicio para el análisis, para mejorar la calidad.
• Cuando existe la necesidad de llamar la atención a los problema o causas de una forma sistemática.
• Al identificar oportunidades para mejorar.
• Al analizar las diferentes agrupaciones de datos (ejm: por producto, por segmento, del mercado, área geográfica, etc.)
• Al buscar las causas principales de los problemas y establecer la prioridad de las soluciones.
• Al evaluar los resultados de los cambos efectuados a un proceso (antes y después)
• Cuando los datos puedan clasificarse en categorías.
• Cuando el rango de cada categoría es importante.

¿CÓMO SE UTILIZA?

1.  Seleccionar categorías lógicas para el tópico de análisis identificado (incluir el periodo de tiempo).

2.  Reunir datos. La utilización de un Check List puede ser de mucha ayuda en este paso.

3.  Ordenar los datos de la mayor categoría a la menor.

4.  Totalizar los datos para todas las categorías.

5.  Calcular el porcentaje del total que cada categoría representa.

6.  Trazar los ejes horizontales (x) y verticales (y primario - y secundario).

7.  Trazar la escala del eje vertical izquierdo para frecuencia (de 0 al total, según se calculó anteriormente), de izquierda a derecha trazar las barras para cada categoría en orden descendente. Si existe una categoría "otros", debe ser colocada al final, sin importar su valor. Es decir, que no debe tenerse en cuenta al momento de ordenar de mayor a menor la frecuencia de las categorías.

8. Trazar la escala del eje vertical derecho para el porcentaje acumulativo, comenzando por el 0 y hasta el 100%

9. Trazar el gráfico lineal para el porcentaje acumulado, comenzando en la parte superior de la barra de la primera categoría (la mas alta)

10. Dar un título al gráfico, agregar las fechas de cuando los datos fueron reunidos y citar la fuente de los datos.

11. Analizar la gráfica para determinar los "pocos vitales"

EJEMPLO DE APLICACIÓN

Un fabricante de Refrigeradores desea analizar cuales son los defectos más frecuentes que aparecen en las unidades al salir de la línea de producción. Para esto, empezó por clasificar todos los defectos posibles en sus diversos tipos:

TIPO DE DEFECTO	DETALLE DEL PROBLEMA
Motor no detiene	No para el motor cuando alcanza temperatura
No enfría	El motor arranca pero la heladera no enfría
Burlete Deficiente	Burlete roto o deforme que no ajusta
Pintura Deficiente	Defectos de pintura en superficies externas
Rayas	Rayas en las superficies externas
No funciona	Al enchufar no arranca el motor
Puerta no cierra	La puerta no cierra correctamente
Gavetas Deficiente	Gavetas interiores con rajaduras
Motor no arranca	El motor no arranca después de ciclo de parada
Mala Nivelación	La heladera se balancea y no se puede nivelar
Puerta Def.	Puerta de refrigerador no cierra herméticamente
Otros	Otros Defectos no incluidos en los anteriores

Posteriormente, un inspector revisa cada heladera a medida que sale de producción registrando sus defectos de acuerdo con dichos tipos. Después de inspeccionar 88 heladeras, se obtuvo una tabla como esta:

TIPO DE DEFECTO	DETALLE DEL PROBLEMA	FREC.
Burlete Defecto	Burlete roto o deforme que no ajusta	9
Pintura Defecto	Defectos de pintura en superficies externas	5
Gavetas Defecto.	Gavetas interiores con rajaduras	1
Mala Nivelación	La heladera se balancea y no se puede nivelar	1
Motor no arranca	El motor no arranca después de ciclo de parada	1
Motor no detiene	No para el motor cuando alcanza Temperatura	36
No enfría	El motor arranca pero la heladera no enfría	27
No funciona	Al enchufar no arranca el motor	2
Otros	Otros Defectos no incluidos en los anteriores	0
Puerta Defecto	Puerta de refrigerador no cierra herméticamente	0
Puerta no cierra	La puerta no cierra correctamente	2
Rayas	Rayas en las superficies externas	4
TOTAL		88

La última columna muestra el número de heladeras que presentaban cada tipo de defecto, es decir, la frecuencia con que se presenta cada defecto. En lugar de la frecuencia numérica podemos utilizar la frecuencia porcentual, es decir, el porcentaje de heladeras en cada tipo de defecto:

TIPO DE DEFECTO	DETALLE DEL PROBLEMA	FREC.	%
Burlete Defecto	Burlete roto o deforme que no ajusta	9	10.2
Pintura Defecto	Defectos de pintura en superficies externas	5	5.7
Gavetas Defecto	Gavetas interiores con rajaduras	1	1.1
Mala Nivelación	La heladera se balancea y no se puede nivelar	1	1.1
Motor no arranca	El motor no arranca después de ciclo de parada	1	1.1
Motor no detiene	No para el motor cuando alcanza Temperatura	36	40.9
No enfría	El motor arranca pero la heladera no enfría	27	30.7
No funciona	Al enchufar no arranca el motor	2	2.3
Otros	Otros Defectos no incluidos en los anteriores	0	0.0
Puerta Def.	Puerta de refrigerador no cierra herméticamente	0	0.0
Puerta no cierra	La puerta no cierra correctamente	2	2.3
Rayas	Rayas en las superficies externas	4	4.5
TOTAL		88	100

Ahora se puede representar los datos en un histograma:

Ahora bien, ¿cuáles son los defectos que aparecen con mayor frecuencia? Para hacerlo más evidente, antes de graficar se pueden ordenar los datos de la tabla en orden decreciente de frecuencia:

Tipo de Defecto	Detalle del Problema	Frec.	%
Motor no detiene	No para el motor cuando alcanza Temperatura	36	40.9
No enfría	El motor arranca pero la heladera no enfría	27	30.7
Burlete Deficiente	Burlete roto o deforme que no ajusta	9	10.2
Pintura Def.	Defectos de pintura en superficies externas	5	5.7
Rayas	Rayas en las superficies externas	4	4.5
No funciona	Al enchufar no arranca el motor	2	2.3
Puerta no cierra	La puerta no cierra correctamente	2	2.3
Gavetas Def.	Gavetas interiores con rajaduras	1	1.1
Mala Nivelación	La heladera se balancea y no se puede nivelar	1	1.1
Motor no arranca	El motor no arranca después de ciclo de parada	1	1.1
Puerta Def.	Puerta de refrigerador no cierra herméticamente	0	0.0
Otros	Otros Defectos no incluidos en los anteriores	0	0.0
Total:		88	100

Se puede ver que la categoría "otros" siempre debe ir al final, sin importar su valor. De esta manera, si hubiese tenido un valor más alto, igual debería haberse ubicado en la última fila.

Ahora resulta evidente cuáles son los tipos de defectos más frecuentes. Se puede observar que los 3 primeros tipos de defectos se presentan en el 82 % de las heladeras, aproximadamente. Por el Principio de Pareto, concluimos que: La mayor parte de los defectos encontrados en el lote pertenece sólo a 3 tipos de defectos, de manera que si se eliminan las causas que los provocan desaparecería la mayor parte de los defectos.

SIMBOLOGÍA DE ELABORACIÓN DE DIAGRAMAS DE FLUJO DE USO GENERALIZADO

HISTOGRAMAS

Un histograma es un gráfico o diagrama que muestra el número de veces que se repiten cada uno de los resultados cuando se realizan mediciones sucesivas. Esto permite ver alrededor de que valor se agrupan las mediciones (Tendencia central) y cual es la dispersión alrededor de ese valor central.

Es básicamente la presentación de una serie de medidas clasificadas y ordenadas, es necesario colocar las medidas de manera que formen filas y columnas, en este caso colocamos las medidas en cinco filas y cinco columnas.

Las manera mas sencilla es determinar y señalar el numero máximo y mínimo por cada columna y posteriormente agregar dos columnas en donde se colocan los números máximos y mínimos por fila de los ya señalados. Tomamos el valor máximo de la columna X+ (medidas maximas) y el valor mínimo de las columnas X- (medidas mínimas) y tendremos el valor máximo y el valor mínimo.
Teniendo los valores máximos y mínimos, podemos determinar el rango de la serie de medidas, el rango no es más que la diferencia entre los valores máximos y mínimos.

Rango = valor máximo – valor mínimo

EJEMPLO:
Rango = 3.67 –3.39 milímetros

Rango= 0.28 N=numero de medidas que conforman la serie N=25

Es necesario determinar el numero de clases para poder así tener el intervalo de cada clase. Ejemplo:

28=4.6 numero de clase 6

intervalo de cada clase 4.6

El intervalo de cada clase lo aproxima a 5 o sea que vamos a tener 6 clases y un intervalo de 5 por clase.

La marca de clase es el valor comprendido de cada clase y se determina así:
X=marca de clase=limite máximo + limite mínimo con la tabla ya preparada se identifican los datos de medida que se tiene y se introducen en la tabla en la clase que le corresponde a una clase determinada.

El histograma se usa para:

• Obtener una comunicación clara y efectiva de la variabilidad del sistema
• Mostrar el resultado de un cambio en el sistema
• Identificar anormalidades examinando la forma
• Comparar la variabilidad con los límites de especificación

Procedimientos de elaboración:

1. Reunir datos para localizar por lo menos 50 puntos de referencia
2. Calcular la variación de los puntos de referencia, restando el dato del mínimo valor del dato de máximo valor
3. Calcular el número de barras que se usaran en el histograma (un método consiste en extraer la raíz cuadrada del número de puntos de referencia)
4. Determinar el ancho de cada barra, dividiendo la variación entre el número de barras por dibujar
5. Calcule el intervalo o sea la localización sobre el eje X de las dos líneas verticales que sirven de fronteras para cada barrera
6. Construya una tabla de frecuencias que organice los puntos de referencia desde el más bajo hasta el más alto de acuerdo con las fronteras establecidas por cada barra.
7. Elabore el histograma respectivo

Supongamos que un médico dietista desea estudiar el peso de personas adultas de sexo masculino y recopila una gran cantidad de datos midiendo el peso en kilogramos de sus pacientes varones:

74.6	74.6	81.6	75.4	69.8	68.4
74.5	85.9	65.8	63.5	95.7	69.4
77.0	113.7	57.8	69.9	74.5	74.3
70.7	77.9	74.5	63.7	77.0	63.2
79.4	76.4	77.0	72.1	70.7	68.4
74.6	95.7	70.7	71.6	79.4	76.9
85.2	78.4	79.4	69.4	74.6	75.4
81.6	84.6	74.6	69.8	85.2	74.8
67.9	97.4	85.2	83.5	81.6	78.9
63.7	74.5	81.6	69.7	67.9	77.0
72.1	77.0	67.9	68.4	63.7	76.7
71.6	70.7	63.7	70.7	72.1	77.0
69.4	79.4	72.1	79.4	71.6	70.7
69.8	74.6	71.6	74.6	69.4	79.4
83.5	85.2	69.4	85.2	69.8	74.6
83.5	81.6	69.8	81.6	83.5	85.2
74.9	67.9	83.5	67.9	79.3	81.6
73.2	63.7	74.9	63.7	76.3	67.9
70.7	70.7	73.2	67.5	79.8	63.7
79.4	79.4	70.7	85.3	70.7	72.1
88.6	74.6	79.4	88.6	79.4	71.6
70.7	85.2	74.6	70.7	74.6	69.4
79.4	81.6	85.2	79.4	85.2	69.8
70.7	67.9	81.6	74.6	81.6	83.5
79.4	63.7	67.9	85.2	67.9	67.9
74.6	72.1	63.7	81.6	63.7	63.7
85.2	71.6	72.1	67.9	72.1	70.7
81.6	69.4	71.6	63.7	71.6	73.2
67.9	69.8	69.4	72.1	69.4	70.7
63.7	83.5	69.8	71.6	69.8	79.4
72.1	83.5	83.5	69.4	83.5	74.6
71.6	69.7	85.2	69.8	69.8	63.7
69.4	68.4	81.6	83.5	83.5	72.1
69.8	70.7	63.7	72.1	83.5	71.6
83.5	79.4	72.1	71.6	72.1	69.4
67.9	71.6	71.6	69.4	71.6	69.8

Así como están los datos es muy difícil sacar conclusiones acerca de ellos.

Entonces, lo primero que hace el médico es agrupar los datos en intervalos contando cuantos resultados de mediciones de peso hay dentro de cada intervalo (Esta es la frecuencia). Por ejemplo, ¿Cuántos pacientes pesan entre 60 y 65 kilos? ¿Cuántos pacientes pesan entre 65 y 70 kilos?:

Intervalos	Nº Pacientes (Frecuencia)
<50	0
50-55	0
55-60	1
60-65	17
65-70	48
70-75	70
75-80	32
80-85	28
85-90	16
90-95	0
95-100	3
100-105	0
105-110	0
>110	1

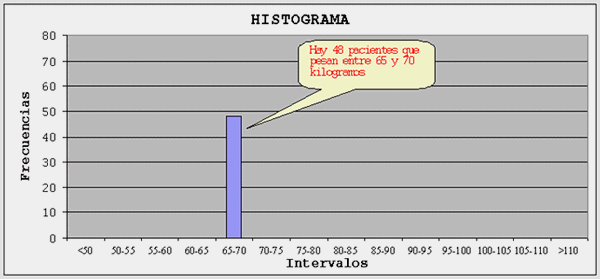
Ahora se pueden representar las frecuencias en un gráfico como el siguiente:

Por ejemplo, la tabla nos dice que hay 48 pacientes que pesan entre 65 y 70 kilogramos. Por lo tanto, levantamos una columna de altura proporcional a 48 en el gráfico:

Y agregando el resto de las frecuencias nos queda el histograma siguiente:

¿Qué utilidad nos presta el histograma? Permite visualizar rápidamente información que estaba oculta en la tabla original de datos. Por ejemplo, nos permite apreciar que el peso de los pacientes se agrupa alrededor de los 70-75 kilos. Esta es la Tendencia Central de las mediciones. Además podemos observar que los pesos de todos los pacientes están en un rango desde 55 a 100 kilogramos. Esta es la Dispersión de las mediciones. También podemos observar que hay muy pocos pacientes por encima de 90 kilogramos o por debajo de 60 kilogramos.

Ahora el médico puede extraer toda la información relevante de las mediciones que realizó y puede utilizarlas para su trabajo en el terreno de la medicina.

CONCLUSIÓN

Los diagramas nos ayudan a solucionar los posibles problemas que se presenten en una empresa, ya que por medio de estos podemos desarrollar una serie de pasas que nos llevan a buscar las soluciones posibles de dicho inconvenientes.

Un diagrama de Causa-Efecto es de por si educativo, sirve para que la gente conozca en profundidad el proceso con que trabaja, visualizando con claridad las relaciones entre los Efectos y sus Causas. Sirve también para guiar las discusiones, al exponer con claridad los orígenes de un problema de calidad. Y permite encontrar más rápidamente las causas asignables cuando el proceso se aparta de su funcionamiento habitual.

Y con los histogramas nos permiten apreciar los datos en unos gráficos y así saber cuantas veces se a repetido el inconveniente , podemos corregir dichos problemas mas rápido elaborando una lluvia de ideas , analizarla cada una y estudiar de cerca el problema para llegar a una conclusión de cuales fueron las causas y efecto que lo originaron y actual de inmediato para no tener mas perdidas de tiempo , ni dinero en una organización , hoy en día los diagramas de causa-efecto son muy utilizados en todos las organizaciones .

 

Ramírez, José

MARACAIBO