- Resumen
- Introducción: No son las
matemáticas las que hacen al
economista - Conceptos
básicos - Deducción de la
ecuación de Slutsky en la teoría del
consumidor - Deducción de la
ecuación de Slutsky con demandas
compensadas - Ecuación de Slutsky
para la oferta de trabajo - Ecuación de
Slutksy en la elección intertemporal - Generalización del
efecto dotación - Análisis de los signos
de los efectos - Conclusiones
- Bibliografía
consultada
Esta monografía tiene como propósito
principal exponer la relevancia de la ecuación de
Slutsky en los términos de Hicks, y mostrar las
diferentes expresiones que puede adoptar la misma, explicando en
cada caso las diferencias y similitudes que puedan existir.
Palabras claves: microeconomía, teoría
del consumidor,
efecto ingreso, efecto sustitución, efecto
dotación, efecto renta, efecto precio, bien
típico, bien giffen, bien normal, bien inferior, Slutsky,
Hicks.
Introducción: No son las matemáticas las que hacen al
economista.
Debo confesar que en mi vida nunca imaginé que
realizaría una monografía
sobre una ecuación. ¿Cual es el motivo que me
impulsa a hacerla? Para entenderlo, primero debemos recordar que
la ciencia
moderna se funda en una precomprensión del sentido de la
realidad en términos de "aquello que puede ser calculado y
medido". Lo real será lo "calculable".
Es por eso que el científico de la modernidad le
asignaba tanta importancia a las matemáticas: "la naturaleza
está escrita en caracteres matemáticos"
sentenció Galileo Galilei
algún tiempo
atrás. Considero que hoy en día pocos
científicos se atreverían a realizar una
afirmación tan categórica.
Sin embargo, el hecho de que las matemáticas
tengan una utilidad limitada
y no sirvan para explicar todas las conductas humanas, y en
nuestro caso particular las conductas económicas, no
significa que la ciencia
matemática
no sea una herramienta provechosa a una ciencia social como lo es
la Economía.
Es por eso que me veo impulsado a realizar esta
monografía, simplemente para mostrar a las
matemáticas como una herramienta que en ciertas ocasiones
sirve para "calcular y medir" fenómenos
económicos.
Esta monografía tiene como propósito
principal exponer la relevancia de la ecuación de Slutsky
en los términos de Hicks, y mostrar las diferentes
expresiones que puede adoptar la misma, explicando en cada caso
las diferencias y similitudes que puedan existir.
Efecto Sustitución y Efecto
Renta
En economía no solo es relevante saber cual
será la conducta de los
agentes en determinadas circunstancias, sino también saber
como variará dicha conducta ante variaciones del entorno.
¿Cuál será la cantidad demandada de un
determinado bien ante variaciones de su precio?
¿Qué efecto tendrá una variación del
salario sobre la
cantidad de empleo
ofrecida? ¿Cuanto cambiara mi ahorro si
cambia la tasa de
interés?
Para llegar a una respuesta es necesario dividir estos
cambios en dos efectos que analizaremos a continuación: el
efecto sustitución y el efecto renta.
Cuando varía el precio de un bien se pueden
observar estos dos efectos: varía tanto la tasa a la que
puede intercambiarse ("sustituir") un bien por otro como el
poder
adquisitivo total de nuestra renta. La variación de la
cantidad demandada por una variación de la relación
de intercambio entre los dos bienes se
denomina efecto sustitución o precio, mientras que la
variación de la demanda
provocada por una variación del poder adquisitivo se
denomina efecto renta o ingreso.
Efecto Sustitución a la Slutsky y a la
Hicks.
Existen dos maneras de ver el efecto sustitución.
Si lo consideramos a la Slutsky, estaremos hablando de la
variación que experimenta la demanda cuando varían
los precios,
manteniéndose constante el poder adquisitivo inicial. Si
lo consideramos a la Hicks, estaremos hablando de la
variación que experimenta la demanda cuando varían
los precios, manteniéndose en un mismo nivel de utilidad,
es decir, en una misma curva de indiferencia. En esta
monografía nos limitaremos únicamente a desarrollar
el análisis basándonos en la postura de
Hicks.
Deducción de la ecuación de Slutsky en
la teoría del consumidor:
Como dije al principio, lo que interesa saber es cual
será el nuevo equilibrio
cuando varíe el entorno que lo determina. Por lo tanto,
debemos hallar las condiciones de equilibrio del sistema y luego
diferenciarlo. Haciendo esto estaremos viendo cuál
será el cambio en las
variables de
decisión del consumidor cuando varían los datos que las
determinan, de modo de seguir cumpliendo las condiciones de
equilibrio, es decir, de seguir optimizando.
En este apartado me limitaré a la
maximización de la utilidad sujeta a restricción
presupuestaria, también llamado problema primal. De dicho
proceso surgen
funciones de
demanda marshallianas, que expresan que la cantidad demandada de
un bien depende de los precios de los bienes en cuestión y
del ingreso disponible, 
Veámoslo analíticamente:
Maximizar 
sujeto a: 
Como es un caso de maximización sujeto a
restricción, formamos un lagrangiano:
Las condiciones de primer orden establecen que las
derivadas
parciales del lagrangiano deben ser cero (aseguran la existencia
de un extremo condicionado), mientras que las condiciones de
segundo orden establecen que dicho extremo es un máximo (y
no un mínimo). El desarrollo de
las condiciones de segundo orden lo omitiremos, ya que asumiremos
que se cumplen.
Así, las condiciones de primer orden
son:
Diferenciando totalmente el sistema
obtenemos:
Este nuevo sistema puede ser expresado como el producto de
dos matrices. Para
verlo, dejaremos las incógnitas en el primer miembro,
dejando en el segundo los datos de las variaciones que han
ocurrido.
Ahora sí, lo expresamos en forma
matricial:
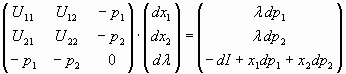
Habiendo expresado el sistema en forma de producto
matricial, podemos resolverlo fácilmente utilizando la
regla de Cramer, mediante la cual podemos despejar cualquiera de
las tres incógnitas, ya sea
, 
o 
.
Desarrollaré el caso para , siendo los demás casos
análogos.
Por comodidad y para simplificar la notación, al
denominador del cociente anterior lo llamaremos simplemente
, que se llama
determinante orlado, siendo 
los menores complementarios de dicho determinante.
El hecho de plantear un problema de maximización implica
necesariamente que el determinante orlado sea positivo. Esto
surge de las condiciones de segundo orden. Si el determinante es
positivo, estamos en una maximización, si es negativo, en
una minimización.
Desarrollando el determinante del numerador
obtenemos:
Esta expresión puede ser manipulada
algebraicamente de modo que quede como la siguiente:
A su vez, podemos observar que varios de los
términos del numerador son iguales a los menores
complementarios. Así pues, podemos escribir la
expresión como:
(1)
Como lo que nos interesa ver es cuanto varía
cuando
varían los precios (y por lo tanto el poder adquisitivo
del ingreso), lo que queremos hallar es, por ejemplo, 
. Este cociente representa
el efecto total directo (se podría también calcular
el cruzado). Dicho efecto total se desagrega en los dos
anteriormente mencionados.
La última expresión (1) a la que arribamos
tras diferenciar el sistema de equilibrio nos permite apreciar
ambos efectos. Observemos que al derivar respecto de 
, es decir, hacer , el segundo término de (1) se
vuelve cero, de forma que:
He aquí la expresión del efecto total
directo, donde el primer termino expresa el efecto
sustitución y el segundo representa el efecto ingreso.
Para afirmar esto nos basamos en que el efecto sustitución
exige que nos mantengamos en la misma curva de indiferencia, de
modo que:
Como en el equilibrio maximizador el cociente entre las
utilidades marginales debe ser igual al cociente entre los
precios, 
entonces
podemos decir que:
Si observamos el sistema diferenciado totalmente podemos
ver que
Como 
podemos decir que 
Por lo tanto el tercer miembro de (1) se vuelve cero. Si
queremos ver el efecto sustitución propio precio, entonces
el segundo termino de (1) también se hará cero.
Finalmente, el efecto sustitución, es decir la
variación de la cantidad demandada ante variaciones del
propio precio de modo que el nivel de utilidad no varíe,
es:
Para observar el porque el efecto renta es el segundo
miembro debemos realizar un procedimiento
mucho mas sencillo. Si pensamos en el efecto renta como las
variaciones de la cantidad demandada al variar el poder
adquisitivo 
por
el total de la cantidad demandada, entonces nos queda que todos
los demás miembros de (1) se vuelven cero cuando hacemos
, quedando
únicamente al que multiplica a 
que es 
. A eso lo debemos multiplicar por la cantidad
demandada, que es
Así llegamos a deducir el Efecto Slutsky en
términos de Hicks.
Como ya dije anteriormente, podemos realizar todo un
procedimiento similar al expuesto para hallar el efecto total
cruzado.
Para resumir esta parte, podemos dejar expresados los
efectos, tanto en forma matricial como en su forma
diferencial.
Efecto Total Directo:
En forma matricial: 
En forma diferencial: 
Efecto Total Cruzado
En forma matricial: 
En forma diferencial: 
Deducción de la ecuación de
Slutsky con demandas compensadas:
En el apartado anterior mostré la forma que
adopta la ecuación de Slutsky cuando utilizamos el
problema primal. Sin embargo no es la única manera de
llegar; también puede hacerse planteando un problema dual,
es decir, minimizar el gasto sujeto a lograr un determinado nivel
de utilidad. Mediante este procedimiento se pueden obtener
funciones de demanda compensadas o hicksianas, 
.
Si se presta atención se puede observar que la demanda
compensada no es otra cosa que el efecto sustitución en
los términos de Hicks, ya que el nivel de utilidad no
varió. Por lo tanto ya estamos en condiciones de escribir
como será la ecuación de Slutsky con demandas
compensadas. Veámoslo para el caso del efecto total
directo del bien 1. Dado que 
simplemente representa la variación de la
cantidad demandada del bien 1 ante variaciones de su precio de
modo que la utilidad no varíe, podríamos expresar
como 
, ya que la demanda
compensada esta sujeta a un nivel de utilidad fijo, de modo que
. De esta forma
podemos escribir la ecuación de Slutsky como 
.
También se puede arribar a este resultado
planteando el problema desde otra perspectiva. Pero para poder
entender el procedimiento que realizaré a
continuación es necesario recordar ciertas identidades y
propiedades existentes entre el problema primal y el
dual.
En el dual existe una función de
gasto 
que es el
nivel mínimo de gasto necesario para alcanzar un
determinado nivel de utilidad, en función de cuales sean
los precios:
.
Además dicha función cumple con el Lema de
Shepard que afirma que la derivada de la función gasto
respecto de un precio es igual a la demanda compensada del bien
cuyo precio varió. En términos matemáticos:
(ver
demostración en el
Apéndice1).
Una importante relación existente entre el
problema primal y el dual es la identidad
ingreso-gasto. Si el nivel máximo de utilidad alcanzado en
el problema primal es el nivel del parámetro de la
restricción del problema dual de minimización,
podemos aseverar que el nivel de gasto minimizado coincide
exactamente con el ingreso del consumidor en el problema primal
de maximización.
Es decir, el gasto mínimo necesario para alcanzar
un nivel dado de utilidad es igual al ingreso del primal que
alcanza dicho nivel de utilidad.
Aplicando todo esto, podemos llegar a la ecuación
de Slutsky de la siguiente manera:
Sabemos que cuando se maximiza la utilidad
también se esta minimizando el gasto (ver
Apendice2). Entonces, la demanda compensada es igual a
la demanda marshalliana para 
Ahora derivamos la demanda compensada respecto de un
precio, utilizando la regla de la cadena, ya que lo que antes era
ingreso ahora es gasto y depende de los precios. Yo aquí
derivaré respecto del propio precio.
Aplicando el Lema de Shepard y recordando la identidad
existente entre el gasto del dual y el ingreso del primal podemos
reexpresar la última ecuación como:
Dado que en el punto de optimización, 
(recordar que cuando se
maximiza la utilidad se esta minimizando el gasto), podemos
escribir la última ecuación, previo reordenamiento
de términos, como sigue:
Que no es otra cosa que lo que planteamos
intuitivamente al comienzo del apartado.
Análogamente al apartado anterior, el efecto
cruzado será:
Ecuación de Slutsky para la oferta de
trabajo:
"La teoría de la
determinación de los salarios en un
libre mercado no es
sino un caso especial de la teoría general del valor. Los
salarios son el precio del trabajo"
J.R. Hicks, The Theory of Wages
(1932)
Hasta ahora estuvimos derivando la ecuación de
Slutsky con un supuesto implícito: que el ingreso estaba
dado exógenamente.
En la realidad las personas obtienen su ingreso
vendiendo cosas, ya sean activos de su
propiedad o su
fuerza
laboral. Es
decir, por un lado demandan bienes y por otro lado los ofrecen.
La diferencia entre lo que demandan y lo que ofrecen se denomina
demanda neta. Si ofrecen más de lo que demandan entonces
la demanda neta es negativa. En tal caso se dice que son
oferentes netos.
Los bienes que pueden ofrecer las personas no son
ilimitados, sino que son escasos. Incluso la fuerza laboral es
limitada. Por lo tanto podemos afirmar que los agentes parten con
dotaciones limitadas de bienes.
Cuando varían los precios, varían los
precios tanto de los bienes que consume como de los que ofrece.
Es decir, se añade un nuevo efecto al análisis que
veníamos efectuando. Por un lado, cambian los precios
relativos, por otro lado cambia el poder adquisitivo del ingreso.
Pero como el ingreso ahora esta determinado endógenamente,
entonces la renta monetaria también varía junto con
la variación de los precios, resultando necesario saber si
el agente es demandante neto u oferente neto del bien en
cuestión.
Por ende es preciso volver a hallar la ecuación
de Slutsky, esta vez teniendo en cuenta este nuevo efecto,
denominado efecto-renta-dotación. Para hacerlo
partiré del problema primal de
maximización.
Las personas poseen una cantidad limitada de tiempo para
repartir entre dos actividades, trabajo u ocio, de modo que
donde 
es la dotación de
tiempo (24 horas por día, por ejemplo), 
es el tiempo destinado a
ocio y 
es el
tiempo destinado a trabajar. El ocio es un bien, mientras que
el trabajo
puede ser considerado un "mal". Sin embargo, el trabajo es lo que
provee ingreso para disfrutar de otros bienes. Por lo tanto el
objetivo del
consumidor es maximizar la utilidad resultante de consumir ocio y
de consumir otros bienes representados por el ingreso 
. Queda claro que la parte
del ocio que no consumimos la dedicamos al trabajo, por lo tanto
al obtener la demanda de ocio estamos a la vez obteniendo la
oferta de trabajo.
Analíticamente tenemos que:
Es decir, la restricción implica que el ingreso
que el individuo
tendrá para consumir otros bienes provendrá de su
salario por el tiempo que trabaje mas un ingreso no laboral
exógenamente dado proveniente, por ejemplo, de familiares
o alquileres.
Para hallar la combinación óptima entre
ingreso y ocio debemos plantear el ya conocido lagrangiano y
luego hallar las condiciones de primer orden:
Las condiciones de primer orden serán:
Las condiciones de segundo orden aseguran la convexidad
de las curvas de indiferencia, lo que a su vez asegura que la
solución sea un máximo y no un mínimo. El
desarrollo de las condiciones de segundo orden lo obviaré
y asumiré que se cumplen.
Partiendo de las condiciones de primer orden se puede
hallar la demanda de ocio, es decir, la oferta de trabajo
(recordar que lo que no es ocio, es trabajo). La demanda de ocio
dependerá del salario vigente y del ingreso no laboral
dado. Es decir, 
,
por lo tanto la oferta de trabajo será: 
.
Hagamos un recuento de las ecuaciones que
tenemos y veamos que manipulaciones matemáticas podemos
hacer para hallar el efecto total desagregado en efecto
sustitución, renta y renta-dotación.
Ecuaciones:
(1) 
es
la ecuación de una curva de nivel
(2) 
es
la ecuación de la restricción presupuestaria ya
vista.
(3) 
es
la ecuación de la demanda de ocio
Lo que queremos hallar ahora es cuanto variará la
demanda de ocio (y por lo tanto la oferta de trabajo), cuando
varían los precios 
, en este caso el único precio es 
(nótese que
es tanto la
retribución al trabajo como el costo del ocio).
El efecto total deberá poder desagregarse en los tres
efectos antes dichos.
Comenzare diferenciando totalmente las tres
ecuaciones:
(1) 
como (surge
de las condiciones de 1° orden), entonces:
; como
. Recordar que
es
mayor
que cero implica que la restricción es efectiva,
es decir, que la solución se da en la frontera del
conjunto alcanzable.
(2) 
Reordenando términos la expresión queda
así: 
Como 
entonces 
Reordenando términos tenemos que: 
(3) 
Dado que 
, entonces 
Dividiendo ambos miembros por 
, tenemos que
(4)
Quizás llame la atención el miembro a la
izquierda de la igualdad.
¿Por qué planteo la derivada de modo que nos
mantengamos en una misma curva de indiferencia? Sencillamente
porque al inicio planteé la ecuación (1), que es la
ecuación de una curva de indiferencia. Por lo tanto todo
el análisis esta planteado de modo que . Eso fue lo que nos
permitió afirmar que , entre otras cosas.
Reordenando los términos de (4) nos
queda:
o lo
que es lo mismo: 
He aquí los tres efectos antes mencionados. El
efecto total es
igual al efecto sustitución 
mas el efecto-renta-dotación 
menos el efecto-renta
ordinario 
Ecuación de Slutksy en la
elección intertemporal:
Hasta ahora estuvimos analizando la ecuación de
Slutsky para la demanda de bienes (ropa, comida, ocio, etc.)
suponiendo que el individuo consume toda su renta en un
único periodo, no dejando cabida al ahorro para consumos
futuros.
En este apartado nos adentraremos en la elección
intertemporal, es decir, el análisis de la conducta del
consumidor respecto a las decisiones relacionadas con el ahorro y
el consumo a lo
largo del tiempo. Éste análisis no difiere en
esencia de la elección individual vista anteriormente. En
vez de buscar la combinación de bienes óptima que
maximiza la utilidad del agente dadas sus preferencias, buscamos
la combinación de cestas (
), integradas por distintos bienes, que
consumirá en cada periodo dada su preferencia
temporal.
En la elección intertemporal también
existen supuestos simplificadores:
- Solo existen dos periodos de tiempo, el hoy, y el
mañana. - Los ingresos del
individuo están dados (son dotaciones), teniendo un
ingreso para cada periodo,
e 
para los periodos cero (hoy) y uno (mañana)
respectivamente. - La posibilidad de pedir prestado dinero o
prestar dinero a una tasa de interés
nominal
es la
bisagra existente entre los dos periodos de tiempo. - El nivel de precios es constante e igual a 1 en ambos
periodos.
e 
es laMatemáticamente el problema aquí se puede
plantear como sigue:
Aquí la restricción implica que el consumo
futuro no puede ser mayor que el ingreso futuro 
mas el ahorro en el
periodo cero junto a los intereses generados por ese ahorro. La
restricción podría manipularse
matemáticamente para expresarla en términos del
consumo presente. Es común que se escriba la
restricción expresándola en términos de
valor actual que es una buena forma de expresar la
restricción presupuestaria intertemporal debido a que mide
el futuro en relación con el presente: 
Para hallar la combinación óptima entre
consumo presente y consumo futuro debemos seguir los ya
familiares pasos de la maximización sujeta a
restricción. Primero formamos el lagrangiano:
Las condiciones de primer orden serán:
Las condiciones de segundo orden, al igual que en los
apartados previos, supondré que se cumplen. El proceso
para hallar la ecuación de Slutsky en la elección
intertemporal es idéntico al utilizado en el apartado de
oferta de trabajo.
De las condiciones de equilibrio se pueden hallar
demandas de consumo temporal, que dependen de la tasa de
interés y las dotaciones de renta: 
.
Debido a que poseemos dotaciones, la ecuación de
Slutsky tendrá un efecto renta-dotación. Así
como en el apartado anterior hablábamos en términos
de oferentes netos y demandantes netos, aquí podemos hacer
lo mismo, en términos de oferentes neto de ahorro
(prestamista) o demandantes netos de ahorro
(prestatario).
Si recordamos que el ahorro (o endeudamiento) es
podríamos
llegar a "adivinar" por mera intuición como
lo hicimos en el apartado con demandas compensadas, y tomando
como referencia la ecuación para la oferta laboral, que la
ecuación de Slutsky es:
Si "adivinásemos" de este modo estaríamos
en lo correcto. La deducción correspondiente figura a
continuación.
Como en la sección anterior, plantearé
tres ecuaciones, las cuales diferenciaré totalmente, y
luego de una pequeña manipulación matemática
se llega a la ecuación de Slutsky tal y como la vinimos
viendo.
(1) 
es
la ecuación de una curva de nivel
(2) es
la restricción presupuestaria en términos de valor
actual.
(3) es
la demanda de consumo en el periodo cero.
(1) 
.
De las condiciones de primer orden surge que 
. Reemplazando en el
diferencial total de (1) se obtiene:
.
Sacando factor común tenemos que:
.
Al igual que en la sección anterior, 
ya que la solución
se da en la frontera y la restricción es efectiva. Por lo
tanto podemos deducir que 
(2) 
La ultima ecuación puede simplificarse mucho, ya
que , y por otra
parte sabemos que 
ya que estamos ubicados en el periodo cero, es decir el presente,
por lo que el ingreso ya fue percibido (y por lo tanto no es una
variable). Dicho esto podemos volver a escribir la
ecuación como:
, o lo
que es lo mismo
Reordenando términos podemos obtener:
Ahora bien, si observamos detenidamente
la restricción presupuestaria podemos apreciar que
Por lo tanto 
(3) 
Como sabemos que y que 
rescribiré el diferencial de (3):
Dividiendo ambos miembros por 
obtenemos:
(4)
Aquí el miembro a la izquierda de la igualdad
tiene el mismo significado que el visto para la oferta laboral.
Debido a que (1) es la ecuación de una curva de
indiferencia, todo el análisis esta planteado de modo que
.
Reordenando términos, la expresión queda
como la vista en otros apartados:
Los efectos (sustitución, renta ordinario y
renta-dotación) pueden apreciarse como en el de la oferta
laboral. El efecto total es 
, el renta ordinario es 
y el renta-dotación es 
.
Generalización del efecto
dotación:
Este tema ya ha sido mencionado en capítulos
previos, mas específicamente en la sección de
oferta de trabajo. En dicha sección proporcioné el
fundamento conceptual-económico del efecto dotación
y posteriormente lo deduje para el caso particular de la demanda
de ocio y en el apartado siguiente para la elección
intertemporal.
En esta parte de la monografía me propongo
explicar la expresión matemática del efecto
dotación de una forma un poco más general que lo
hecho anteriormente. Pero antes de hacerlo creo que resulta
conveniente, a riesgo de ser
reiterativo, volver a repasar el la naturaleza del efecto que nos
convoca.
Un agente económico parte con dotaciones de
bienes 
que vende
en el mercado a los precios 
, obteniendo así su ingreso 
, el cual utilizará
para comprar bienes que consumirá 
. Como estamos bajo el supuesto que
solamente existen dos bienes lo que realmente compre en el
mercado es la demanda neta, que se expresa como la diferencia
entre lo que consume (demanda bruta) y lo que posee, es decir
. Nótese
que mientras que las demandas brutas son positivas, la demanda neta puede ser
negativa en caso que la dotación supere lo que consume. Es
decir, ofrece mas de lo que demanda, por lo tanto es oferente
neto.
La cantidad de bienes que se pueden consumir
están limitadas por su ingreso , que es igual al valor de su
dotación. Por lo tanto 
.
En esta ecuación la dotación esta
determinada exógenamente, por lo tanto variaciones de la
dotación (que implican variaciones del ingreso nominal)
manteniéndose fijos los precios hace las veces de las
variaciones exógenas del ingreso para el modelo
sencillo en el cual el ingreso estaba determinado por fuera del
modelo.
Observemos que ahora el ingreso monetario esta
determinado endóngenamente: una variación de
precios implica una variación de la tasa de intercambio
entre ambos bienes (corresponde al efecto sustitución),
una variación de poder adquisitivo (corresponde al efecto
renta-ordinario), pero también una variación del
valor de la dotación y por ende una variación del
ingreso nominal (corresponde al efecto
renta-dotación).
Es decir, podemos definir al efecto
renta-dotación como la variación que experimenta el
ingreso nominal cuando varían los precios por la
variación que sufre la demanda cuando varía el
ingreso.
El efecto total es la suma de estos tres efectos, dos de
los cuales nos deben ser familiares a esta altura.
Efecto total = efecto sustitución + efecto renta
ordinario + efecto renta dotación
Si volvemos a la definición del efecto
dotación nos damos cuenta que es el producto de dos
derivadas: 
Recordando que podemos afirmar que
, por lo que el efecto renta-dotación es
, de modo que el
efecto total directo es:
O lo que es lo mismo:
Recuérdese que la expresión 
es la demanda neta, por lo
tanto el efecto renta (ordinario mas dotación) depende de
si el bien en cuestión es normal o inferior y si estamos
siendo oferentes netos o demandantes netos.
Análisis de los signos de los
efectos:
De los signos de los efectos de la ecuación de
Slutsky se pueden extraer importantes conclusiones acerca de los
bienes en cuestión, como es agruparlos en ciertas
categorías a saber: normales, inferiores, típicos,
giffen, sustitutos, complementarios.
Efecto de la variación del propio
precio:
Veamos primero el significado del signo del efecto
sustitución. Se puede afirmar que el efecto
sustitución propio precio es siempre no positivo, es
decir, puede ser cero o negativo. Esta afirmación sale del
hecho de que las curvas de indiferencia tienen pendiente
negativa. Recordemos que las curvas de indiferencia tienen
pendiente negativa porque trabajamos con el supuesto de "no
saturación" donde "mas se prefiere a menos".
Es decir, en términos
matemáticos, las utilidades marginales de los bienes son
positivas, por lo tanto, por regla de la cadena, 
.
En términos económicos, cuando se alteran
los precios relativos existe una tendencia a sustituir otras
mercancías por aquella cuyo precio ha bajado. Es decir,
los bienes en cuestión son sustitutos netos.
El adjetivo neto se refiere a que estamos teniendo en cuenta
únicamente el cambio de los precios relativos (efecto
sustitución).
El signo del efecto renta ordinario es un poco mas
intrincado.
- Cuando el efecto ingreso varía en el mismo
sentido que el efecto sustitución, es decir
, se
dice que el bien es normal. Los bienes normales
son los bienes cuyo consumo aumenta conforme aumenta la
renta. Observemos que si
. - Económicamente estamos diciendo que si baja el
precio de un bien, por un lado aumenta su consumo debido a que
se dejan de comprar los bienes que ahora son relativamente
más caros, y por otro lado, al aumentar nuestro ingreso
real aumentamos el consumo debido a que el bien es normal. El
efecto total tendrá signo negativo, lo que implica que
la curva de demanda tiene pendiente negativa. En dicho caso el
bien se denomina típico. - También puede ocurrir que el efecto ingreso
varíe en sentido inverso al efecto sustitución,
es decir
, se
, por lo que el bien en cuestión se denomina
inferior. Los bienes inferiores son aquellos cuyo
consumo disminuye conforme aumenta la renta. Este tipo de bienes
se caracteriza por poseer una calidad "de
segunda" o "inferior" que otros tipos de bienes.
Para citar un ejemplo, la margarina es un bien
inferior, cuya calidad es menor que la de la manteca. Cuando
aumenta el ingreso el consumidor deja de comprar margarina y
comienza a consumir manteca. Del hecho de que el efecto renta
sea positivo y por lo tanto varíe en sentido contrario
al efecto sustitución se deduce que el efecto total
quedara indeterminado. La magnitud del efecto ingreso reside
parcialmente en la importancia dentro del presupuesto de
la mercancía en cuestión. Si tiene una gran
importancia, el efecto ingreso tendrá mas peso dentro
del efecto total.
- Si el bien es efectivamente inferior y el valor
absoluto del efecto ingreso supera al del efecto
sustitución, entonces el efecto total tendrá
signo positivo. Es decir, ante disminuciones del precio,
disminuye la cantidad demandada, por lo que la curva de
demanda tendrá pendiente positiva (al menos en un
tramo). Este tipo de bienes se denominan
Giffen. Este fenómeno que "rompe" con la
ortodoxa curva de demanda con pendiente negativa se da en
pocas situaciones donde el nivel de vida de los consumidores
es muy bajo y satisfacen sus necesidades, por ejemplo, de
alimentación, con un único bien
de uso general (el pan, o las papas). Cuando cae el precio de
dicho bien, su ingreso real aumenta y le permite consumir una
dieta mas variada, reduciendo la cantidad demandada del
bien. - Si el efecto renta no llega a contrarrestar
totalmente al efecto sustitución el efecto total tiene
signo negativo, por lo que la curva de demanda tiene
pendiente negativa, siendo el bien típico.
El análisis del signo del efecto
renta-dotación es similar al efectuado para el efecto
renta-ordinario, pero con todos los signos cambiados. Vale
decir:
- Cuando el bien es inferior, el efecto renta
dotación varía en el mismo sentido que el efecto
sustitución. Observemos que si cae el precio del bien,
el valor de la dotación disminuye, por lo que disminuye
el ingreso nominal del consumidor, lo que genera que aumente la
cantidad demanda del bien, ya que es inferior. - Cuando el bien es normal, el efecto renta
dotación varía en sentido opuesto al efecto
sustitución. Cuando aumenta el precio del bien, aumenta
el valor de la dotación y por lo tanto aumenta el
ingreso. Al aumentar el ingreso aumenta la cantidad demandada
del bien, que es normal.
Del análisis de signos de los efectos renta
ordinario y dotación se desprende que saber si el
consumidor es un oferente neto o un demandante neto tiene una
gran importancia a la hora de determinar su comportamiento
ante cambios del precio con bienes inferiores o normales. Si es
demandante neto, se comportara conforme al primer análisis
efectuado (el del efecto renta ordinario). Si es oferente neto,
conforme al segundo, correspondiente al efecto
renta-dotación.
Efecto de la variación del precio del otro
bien:
Veamos el signo del efecto sustitución cruzado.
Se puede afirmar que el signo del efecto sustitución
cruzado será siempre no negativo. La justificación
tanto matemática como económica es análoga
al efecto sustitución propio precio. Si cuando se alteran
los precios relativos existe una tendencia a sustituir otras
mercancías por aquella cuyo precio ha bajado, entonces
cuando aumenta el precio del bien 1, aumenta la cantidad
demandada del bien 2, siendo entonces la relación
positiva, siendo los bienes en cuestión sustitutos
netos.
Respecto del signo del efecto renta ordinario y el
efecto renta dotación no hay mucho mas para decir, ya que
es un caso casi idéntico al directo. La suma de ambos
efectos dará como resultado el producto entre la demanda
neta del bien cuyo precio varió y la derivada del bien en
cuestión respecto del ingreso. Analíticamente, la
suma de ambos efectos renta (ordinario y dotación) para el
caso en que varió el precio del bien 1 y se quiere
averiguar el efecto que ésta variación tuvo en el
bien 2, sería: 
De forma que el signo del efecto dependerá de la
demanda neta del bien cuyo precio varió y de si el bien 2
es normal o inferior.
A su vez, la suma de los tres efectos nos da información acerca de cómo son los
bienes entre si. Si cuando aumenta el precio del bien 1 aumenta
la demanda del bien 2, entonces los bienes en cuestión son
sustitutos brutos. El adjetivo bruto se refiere a
que estamos teniendo en cuenta todos los efectos existentes.
Ejemplo de bienes sustitutos brutos pueden ser la carne vacuna y
el pollo. Cuando aumenta el precio de la carne vacuna, aumenta la
demanda de pollo, es decir, se sustituye la carne por el pollo.
Si cuando aumenta el precio del bien 1 disminuye la demanda del
bien 2, entonces los bienes en cuestión son
complementarios brutos. Ejemplo de bienes
complementarios brutos pueden ser las impresoras y
su tinta.
Para una mejor comprensión partiré del
planteo del problema dual hasta llegar a las condiciones de
primer orden
Como es un caso de optimización
(minimización) sujeto a restricción, se puede
resolver fácilmente con el método de los multiplicadores de
Lagrange. Primero formamos el Lagrangiano:
Las condiciones de primer orden
serán:
De las dos primeras ecuaciones surge que
Ya planteados los requisitos de primer orden estamos
en condiciones de demostrar el Lema de Shepard.
Ahora bien, como
entonces:
Prestemos especial atención al ultimo
término:
Dado que estamos trabajando con
entonces sabemos que
por lo que
, de modo que
, quedando
así demostrado el Lema de Shepard.- Demostración del Lema de Shepard:
Las condiciones de primer orden del problema dual
son:
Las condiciones de primer orden del problema primal
son:
Debido a que tanto las condiciones del dual como las
condiciones del primal exigen que el optimo se halle en el
punto de tangencia entre la TMS y la recta presupuestaria,
podemos afirmar que cuando se maximiza utilidad se esta a la
vez minimizando gasto, y viceversa. En palabras del famoso
economista Paul Samuelson: "…la utilidad (si los
gastos
están dados) tan solo se lleva al máximo cuando
se alcanza un determinado nivel en la forma mas barata; vale
decir, cuando los gastos son mínimos para cualquier
nivel de utilidad. Si no fuera así, el consumidor
podría alcanzar el mismo nivel con algo de dinero
sobrante y utilizar tal resto en la adquisición de mas
bienes: podría alcanzar, pues, un nivel de utilidad
mas elevado…"Gráficamente se puede ver de la siguiente
forma:
- "En el punto de optimización,
" - Aclaraciones: a lo largo de la monografía, y
por cuestiones de comodidad, deduje siempre el efecto total
directo. Sin embargo creo que es importante por lo menos dejar
asentado como son las ecuaciones en términos mas
generales, tanto el efecto total directo como el cruzado,
incluyendo el efecto dotación.
entonces sabemos que
por lo que
, de modo que
, quedando
Efecto total directo: 
Efecto total cruzado: 
Además creo necesario aclarar que en distintas
partes se ha utilizado de forma indiferente la notación
o 
para representar el
ingreso.
Por ultimo, y no menos importante, la
monografía se ha visto limitada al caso simplificado de
elección entre dos bienes. Si se quisieran tener en
consideración mas bienes se deberían revisar
varios aspectos, como la no positividad del efecto
sustitución directo y la no negatividad del efecto
sustitución cruzado.
A modo de cierre de este trabajo me gustaría
abusar de un par de citas del libro de Max
Hermann mencionado en la bibliografía utilizada. En
un capítulo acerca de las matemáticas como
método auxiliar a la economía el autor insiste en
prestar atención a que "…el resultado de una
deducción matemática debe ser interpretada con
criterio económico, ya que su interpretación en sentido meramente
lógico-formal puede conducir a conclusiones que no se
compadecen con la realidad…" y "…que afortunadamente la
economía esta muy lejos de poder convertirse en
‘ciencia exacta’, pues si lo hiciera, ello
significaría la perdida total de su carácter de ciencia social por la
eliminación del factor humano."
Coincido totalmente con las afirmaciones del autor y
espero que este trabajo, pese a su grado de abstracción
matemática, sea considerado como un instrumento
matemático al servicio de la
economía, nunca al revés.
Otra de las cosas que intenté remarcar en el
trabajo es la importancia de la "instinto", "intuición" o
"adivinación" a la hora de las deducciones, ya sean
matemáticas como lo fueron en este trabajo, o
económicas. Respecto a este asunto me parece valioso citar
un estudio necrológico de Ragnar Frisch, dedicado a Joseph
Schumpeter, donde al referirse a la posición de este sabio
frente a la econometría –la ciencia que representa
una combinación de teoría económica,
estadística y matemática-
encontramos estas frases:
"Las matemáticas – hasta la forma mas
refinada de matemáticas – son una herramienta
necesaria, pero no mas que una herramienta. Ninguna clase de
tecnicismo matemático, por muy refinado que sea,
podrá jamás reemplazar la intuición, esa
función inexplicable que tiene lugar en el cerebro de un
gran intelecto que, al mismo tiempo, entiende matemáticas
y teoría económica en un sentido mas ortodoxo y que
ha vivido suficiente tiempo (o mejor dicho, con intensidad
suficiente) como para acumular experiencia humana y sentido para
los hechos."
- Rubén H. Pardo, La Posciencia: el
conocimiento científico en las postrimerías
de la modernidad, Ed. Biblos. - Hermann Max, Investigación
económica, su metodología y su técnica,
1° edición, 1963, Fondo de Cultura
Económica. - Hal R. Varían, Microeconomía
Intermedia, 3° edición, Antoni
Bosch. - Fernández de Castro, Juan Tugores,
Fundamentos de Microeconomía, 2°
edición, 1992, McGraw-Hill - Paul Samuelson, Fundamentos del Análisis
Económico, Ed. El Ateneo - Presentaciones PowerPoint
suministradas por la cátedra.
Leandro Ezequiel Brufman
Materia: Microeconomía I
Universidad Nacional del Sur (UNS)
Año:2004