Ecuaciones diferenciales. Aplicaciones a transitorios de circuitos
Primera Parte
1. Estudio de
transitorios de circuitos.
a.- Circuito resistivo-inductivo
serie.
La forma general de un circuito RL serie bajo
excitación de tensión es la siguiente:

La respuesta a
esta excitación de tensión será una
corriente i que producirá sobre la resistencia y
sobre la inductancia sendas caídas de tensión, las
cuales vendrán dadas respectivamente por:
![]()
![]()
Si aplicamos al circuito la segunda ley de Kirchoff,
tendremos que el valor
instantáneo de la tensión en función
del tiempo
será:
![]()
En esta última expresión
observamos:
1.- La respuesta a la transición depende de una
ecuación diferencial lineal de primer orden, donde este,
viene dado por la cantidad de elementos reactivos del
circuito.
2.- Debido a que hay una excitación v, la
ecuación es no homogénea lo cual dificulta su
resolución.
Analizaremos ahora el comportamiento
de este circuito bajo diversos tipos de
excitación.
2.-
Circuito R L serie sin excitación con condiciones
iniciales no nulas.
Este caso es denominado: Régimen
natural
Partamos del siguiente circuito:
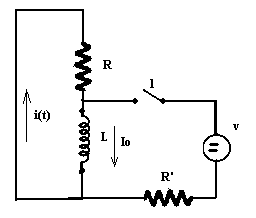

Luego de un tiempo prolongado de funcionamiento
circulará una corriente Io como la indicada en
el circuito. En un determinado instante que designamos con t =0
se abre la llave l, de forma tal que en la bobina se
cumplirá:
t = 0 entonces i =
Io
Bajo estas condiciones estudiaremos como varía la
corriente i en función del tiempo a través del
circuito que contiene a la resistencia R.
El circuito, queda así librado a la única
acción
de la energía concentrada en el campo
magnético de la bobina la cual retorna al circuito
disipándose progresivamente en el resistor en forma de
calor.
Del párrafo
anterior sabemos que:
![]()
Pero en este caso v = 0, por lo tanto:
![]()
Esta última ecuación diferencial es
lineal, de primer orden y homogénea, la cual puede
resolverse separando diferenciales, es decir, se procede como
sigue:
![]()
![]()
Para resolver esta ecuación integramos ambos
miembros, con lo que obtenemos:
![]()
El valor de la constante de integración K, lo obtenemos aplicando a la
última expresión las condiciones iniciales, es
decir:
t = 0 entonces i = Io por lo
tanto
ln Io = K
valor este que remplazando en la expresión
anterior, nos da:
![]()
operando en esta última expresión
obtenemos:
![]()
de donde:
![]()
Es decir que el proceso tiene
una variación exponencial , se inicia cuando la
relación de intensidades es uno para t = 0 y tiende
asintóticamente a cero tal cual se puede observar en el
gráfico:


Hallemos ahora el valor de la subtangente, en el
triángulo formado en la figura por los ejes y la recta
tangente a la curva en t = 0, observemos:
tg = St / 1 de donde St = 1 . tg
a)
por otro lado:

(b)
Relacionando las expresiones (a) y (b), llegamos a la
conclusión:
![]()
donde la subtangente es el tiempo al cabo del cual el
valor final de la corriente es nulo si el decrecimiento en lugar
de ser exponencial se verifica en forma lineal con la misma
pendiente del instante t = 0.
A dicho tiempo se lo llama constante de
tiempo y su unidad es el segundo. Es posible demostrar que no
solamente para t = 0, sino para cualquier otro instante, la
subtangente continua tomando el mismo valor, es decir, que la
constante de tiempo es una característica de los
parámetros del circuito y jamás del tipo de
excitación.
Dijimos que si el proceso fuese lineal al cabo de t =
segundos, la corriente sería nula, pero
debido a la naturaleza
exponencial del fenómeno el valor será:

Es decir que al cabo de un tiempo la
corriente se reduce en un 36,8 % del valor inicial, o
también que existe una reducción del 63,2% del
valor total.
En definitiva, la intensidad en función del
tiempo, vendrá dada por:
![]()
![]()
Las caídas de tensión instantáneas
en las resistencias y
en la inductancia en función del tiempo,
serán:
![]()
Grafiquemos estas tres expresiones en función del
tiempo:

3.- Circuito R L serie con excitación
escalón y condiciones iniciales nulas.
La excitación escalón corresponde a la
siguiente expresión matemática:
t
entonces
u (t) = 0
t > 0 entonces e (t) = V

Partimos como siempre de la expresión:
![]()
siendo nuestro circuito el siguiente:

Esta última expresión, es una
expresión diferencial no homogénea, lineal de
primer orden, la cual para resolverla requerirá una previa
separación de variables tal
cual se indica en las operaciones que
haremos.
![]()
![]()
![]() por tanto
por tanto 
integrando ambos miembros:
![]() (1)
(1)
Resta ahora aplicar las condiciones iniciales, es
decir:
para t = 0 i = 0
y con esto determinar K:
![]() por tanto
por tanto ![]()
reemplazando el valor de K en ( 1 ):
![]()
multiplicando por – l esta última
expresión y operando llegamos a :


![]()
luego, la caída de tensión en la
resistencia será:
![]()
y la caída de tensión en la bobina
será:
![]()
Representando estas tres expresiones gráficamente
obtendremos:


Cabe, ahora, hacer las siguientes consideraciones como
conclusión:
1.-Tanto i como vr y vl tienen dos
términos, el primero que no es función del tiempo
(en el caso del vl vale cero) y describe el
comportamiento final del circuito. Corresponde al régimen
permanente también llamado estacionario o forzado. Por
ejemplo la corriente forzada será igual a V/R y responde
justamente a la ley de 0hm.
2.- El segundo término describe el régimen
natural del circuito el que depende primero de las condiciones de
excitación, de las condiciones iniciales y de los
parámetros circuitales.
3.- La superposición de ambos regímenes da
el comportamiento durante la transición.
4.- la corriente crece desde cero hasta V / R en forma
exponencial. El régimen de crecimiento, está dado
por la constante de tiempo = L / R que depende
exclusivamente de los parámetros circuitales.
5.- La tensión en la resistencia varía de
cero a V siguiendo la misma ley.
6.- La tensión en la bobina disminuye de V a cero
siguiendo la misma ley. Debido a que en el instante inicial, la
tensión aplicada cae totalmente en la bobina y luego
disminuye en forma exponencial.
7.- Se cumple la segunda ley de Kirchoff, es decir la
suma de los valores
instantáneos de vr y vl es constante
e igual a V en el circuito.
4.- Circuito R L serie con excitación
escalón y condiciones iniciales no
nulas
Este es el caso para el cual:
en t = 0 entonces i = +/- Io
será menester para este caso
determinar nuevamente la constante de
integración.
El circuito a emplear será el
siguiente:

Para calcular la constante de integración
nos basaremos en la expresión (1 ) del párrafo
anterior, es decir:
![]()
Aplicando a esta expresión las condiciones
iniciales:
en t = 0 entonces i = +/- Io
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
por tanto
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Remplazando esta última expresión en la
expresión (1 ) tendremos:
Para ver las
fórmulas seleccione la opción ¨Descargar
trabajo¨
del menú superior
Graficando esta última expresión en
función del tiempo para distintos valores de
Io, tendremos los siguientes diagramas:

5.- Circuito R C serie
La forma general de este circuito bajo excitación
de tensión será el siguiente:

Aplicando la segunda ley de Kirchoff a este circuito,
tendremos:
v (t) = vr +
vC
Donde vC es la caída de tensión
en el capacitor y vr =i . R es la caída de
tensión en la resistencia. De la definición de
corriente sabemos que:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
y de la definición de capacidad:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
llegamos a la siguiente expresión de la
corriente:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
que remplaza en la expresión de vr
da:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
y en definitiva:
![]()
La cual es una ecuación diferencial lineal de
primer orden y no homogénea. Todas las conclusiones
sacadas para el circuito R L son válidas para este
circuito.
6.-
Circuito R C sin excitación con condiciones iniciales no
nulas.
Régimen natural.
Este circuito a estudiar queda librado a la
acción de la carga:
Qo = C . Vo
que almacena el capacitor.
Su energía E = ½ C. Vo
2 se disipa en el resistor y el circuito de estudio
será el siguiente:

A partir de la ecuación diferencial del
párrafo anterior trataremos de estudiar la ley de
variación de la tensión en el capacitor y la de la
corriente del circuito, para ello tendremos:
![]()
Pero la excitación del circuito es nula, es
decir, llegamos a la siguiente expresión, la cual es una
ecuación diferencial, lineal de primer orden y
homogénea, lo cual facilita su resolución por
separación de variables:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
integrando esta última expresión
obtenemos:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
donde K es la constante de integración la cual
será determinada como siempre a partir de las condiciones
iniciales; para nuestro caso:
para t = 0 es vc =
Vo
es decir: K = ln Vo
Por lo tanto remplazando el valor de la constante K en
la expresión respectiva, llegamos a :
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
de donde
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Donde = C. R es la constante de tiempo de un
circuito R C serie, es decir es le tiempo en que la
tensión del condensador en descarga se reduce a un 36,8%
del valor inicial o en carga aumenta en un 63,2% del valor de la
tensión final partiendo de cero.
La ley de variación de la intensidad
vendrá dada por:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Por otro lado la caída de tensión en la
resistencia será: ![]()
Representando gráficamente estas expresiones
obtenemos:


7.- Circuito R C serie con excitación
escalón y condiciones iniciales nulas.
Para este caso el circuito bajo excitación de
tensión es el indicado en la figura:

Donde como siempre se cumple la segunda ley de Kirchoff,
es decir:
![]()
![]()
Ecuación esta última diferencial, lineal,
de primer orden, y no homogénea debido a la
excitación de tensión, excitación esta, de
tipo escalón, es decir:
v (t) = V
Para resolver esta ecuación diferencial tendremos
que separar variables, es decir, operamos de la siguiente
manera:
![]() de donde
de donde ![]()
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
integrando esta última expresión, llegamos
a :
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Donde K es la constante de integración y la
determinamos aplicando en la ecuación anterior las
condiciones iniciales, es decir:
Para t = 0 es vc =
0
por lo tanto:
0 = ln (-V) + K por lo tanto K = – ln
(-V)
Expresión esta última que remplazada en la
anterior queda:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
y en definitiva:
vc = V – V . e–
t /
Expresión esta que nos indica la variación
exponencial de la tensión en función del tiempo.
Para t = 0, vc será cero y veremos que toda la
tensión cae en la resistencia; luego vc
irá aumentando y en definitiva para t tendiendo a infinito
la tensión de la fuente caerá totalmente en el
capacitor.
La expresión en función del tiempo que nos
identifica la variación de la intensidad
será:

o sea:
![]()
y la caída de tensión en la resistencia
será:
vr = i . R
![]()
Funciones todas
estas que graficadas, adoptan la siguiente
configuración:


8. Circuito R C serie excitación
escalón y condiciones iniciales no
nulas.
Para este caso el circuito será el que
sigue:

Para resolver este caso directamente habrá que
variar la aplicación de las condiciones iniciales en el
cálculo
de la constante de integración. Las nuevas condiciones
iniciales serán:
Para t = 0 será vc =
+/- Vo
Es decir, aplicando a la siguiente ecuación estas
condiciones tendremos:
![]()
![]()
![]()
es decir:
![]()
![]()
![]() (1)
(1)
Donde el valor de la corriente en
función del tiempo será:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Por otro lado, la caída de tensión en la
resistencia vendrá dada por:
vr = i . R
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Graficando la expresión (1 )
tendremos:

Tomemos es siguiente circuito RL serie:
v(t)

y la fuente lo excita con una tensión senoidal
:
![]()
donde es la separación que existe
entre el origen de coordenadas y el valor máximo de v(t) y
lo medimos desde el máximo de la función v(t) al
origen, de esta forma pueden acontecer dos casos:

Sabemos que en este circuito:
![]()
y a causa de la excitación senoidal:

![]() (1)
(1)
Sabemos además, que la intensidad total en todo
momento será igual a la suma de la componente natural y la
componente forzada:
![]()
de donde, la componente natural es:
![]()
con = L / R
La componente forzada será:
![]() (2)
(2)
donde es el ángulo de fase de la
carga RL del circuito.
Al cabo de un tiempo
t>>5., la transición acaba,
la corriente natural tenderá a cero y la corriente total
tenderá a la forzada. Reemplazando (2) en (1) y
operando:
![]()
![]() (3)
(3)
Por trigonometría sabemos que:
![]()
si en (3) hacemos: ![]() tendremos:
tendremos:
![]()
En esta última expresión y a partir de la
igualdad,
tenemos:
![]()
![]()
donde: ![]()
luego, como enunciamos en hojas anteriores: ![]()
![]()
donde el valor de K lo determinamos a partir de las
condiciones iniciales, es decir si para el instante inicial o sea
t=0 tenemos que i=0 :
![]()
por lo tanto:
![]()
es decir:
![]()
El valor inicial de la componente forzada
será:
![]()
y el de la componente natural:
![]()
Puede ocurrir que
o
o
o ; en
los siguientes gráficos en los que representamos las
corrientes: natural, forzada y total observamos los dos primeros
casos.
1.-

i (intensidad total) in (intensidad
natural) if (intensidad forzada)

i (intensidad total) in (intensidad natural)
if (intensidad forzada)
A partir d estas intensidades de corriente podemos
determinar las respectivas caídas de tensión que
las mismas provocan en los elementos del circuito.
Este fue otro ejemplo en el que aplicamos un modelo
matemático: el que proporcionan, en este caso, las
ecuaciones
diferenciales para resolver el problema de los efectos
transitorios en los circuitos
eléctricos.
Dejo para ustedes, futuros ingenieros, demostrar que la
tensión aplicada a una lamparita en el preciso instante en
que se la enciende es 2.Vmax
Que cosa los transitorios …..
¿no? …………….
Autor:
Prof. Carlos A. Garbarello
Profesor Titular de la cátedra de Laboratorio de
Mediciones Eléctricas II
Escuela Técnica Nº 9 "Ing. Luis A.
Huergo"
Secretaría de Educación del
Gobierno
Autónomo de la Ciudad de Buenos Aires
