- Definiciones
- Teoremas sobre
rangos - Método de
eliminación de Gauss - Método de Gauss –
Jordan - Método de
Gauss-Seidel - Ecuaciones Lineales
Homogéneas - Ecuaciones lineales no
homogéneas - Análisis
insumo-productos estático
intersectoriales - La Condición de
Hawking-Simon - Productos y precios
teoría y aplicaciones - Clasificaciones de los productos
de consumo - Clasificaciones de los
productos industriales - Precio
- Estrategias de
fijación de precios
Es aquella en donde en cada término de la
ecuación aparece únicamente una variable o
incógnita elevada a la primera potencia. Por ejemplo:a 11 X1 + a 12 X2 + a 13 X3 +
… + a 1n Xn = C1 (1)Es una ecuación algebraica lineal en las
variables X1, X2, X3, … , Xn. Se admite
que los coeficientes a11, a12, a13, … , a1n y el
término independiente C1, son constantes
reales.- ECUACIÓN
ALGEBRÁICA LINEAL

Es un conjunto de ecuaciones que deben resolverse
simultáneamente. En los sucesivo se
considerarán únicamente sistemas de
ecuaciones algebráicas lineales, o sea conjuntos de ecuaciones de la
forma:a11 X 1 + a 12 X2 + a13 X 3 +… +
a 1n X n = C 1 (a)a 21 X 1 + a 22 X 2 + a 23 X 3 +…
+ a 2n X n = C 2 (b) (2)…
a n1 X 1 + a n2 X 2 + a n3 X 3 +
… + a nn X n = C n (c)Aplicando la definición de producto
entre matrices, este sistema
de n ecuaciones algebraicas lineales con
n incógnitas puede escribirse en forma
matricial.Para ver la fórmula
seleccione la opción "Descargar" del menú
superior(3)
Este sistema de ecuaciones puede escribirse
simbólicamente como:A X =
C (4)en donde A se llama Matriz
del Sistema. La matriz
formada por A, a la que se le ha agregado
el vector de términos independientes como
última columna, se le llama la Matriz Ampliada
del Sistema, que se representa con (A,
C).Entonces la matriz ampliada
será:Para ver la fórmula
seleccione la opción "Descargar" del menú
superior - SISTEMA DE
ECUACIONES - SOLUCIÓN DE UN SISTEMA DE
ECUACIONES
Es un conjunto de valores de
las incógnitas que verifican simultáneamente a
todas y cada una de las ecuaciones del sistema.
De acuerdo con su solución, un sistema puede
ser: Consistente, si admite solución; o
Inconsistente, si no admite
solución.
Un sistema Consistente puede ser:
Determinado, si la solución es única o
Indeterminado, si la solución no es
única. En este caso se demuestra que existe una
infinidad de soluciones.
El rango de una matriz es el orden de determinante no
nulo de mayor orden que puede obtenerse de esa matriz. El rango
de la matriz A se representa con la
notación r(A) y el de la matriz
ampliada con r(A, C).
En álgebra
se demuestra que:
- Para cualquier sistema,
(*)
- Si r(A) < r(A, C) el sistema es
inconsistente - Si r(A) = r(A, C) el sistema de
ecuaciones es consistente
En este caso, si además r(A) =
n, el sistema es determinado e
indeterminado si r(A) < n, siendo
n el número de variables en el
sistema.
En general, hay dos tipos de técnicas
numéricas para resolver ecuaciones simultáneas:
Directas, que son finitas; e Indirectas, que
son infinitas.
Naturalmente, ninguna técnica práctica
puede ser infinita. Lo que queremos decir es que en un
principio los métodos
directos (despreciando errores por redondeo) producirán
una solución exacta, si la hay, en un número
finito de operaciones
aritméticas.
Por otra parte, un método
indirecto requerirá en principio un número
infinito de operaciones aritméticas para producir una
solución exacta. Dicho de otra manera, un método
indirecto tiene un error por truncamiento mientras que un
método directo no lo tiene.
Sin embargo, la expresión "en principio" del
párrafo anterior es crucial: en realidad
se tienen errores por redondeo. Tendremos que considerar
más cuidadosamente esta cuestión. En un sistema
grande, mal comportado, los errores por redondeo de un
método directo puede hacer que la "solución"
carezca de sentido. A pesar de su error teórico por
truncamiento, un método indirecto puede ser mucho
más deseable porque en él los errores por
redondeo no se acumulan.
El primer método que se presenta usualmente en
álgebra, para la solución de ecuaciones
algebraicas lineales simultáneas, es aquel en el que se
eliminan las incógnitas mediante la combinación
de las ecuaciones. Este método se conoce como
Método de Eliminación. Se denomina
eliminación Gaussiana si en el proceso de
eliminación se utiliza el esquema particular atribuido a
Gauss.
Utilizando el método de Gauss, un conjunto de
n ecuaciones con n
incógnitas se reduce a un sistema triangular
equivalente (un sistema equivalente es un sistema que
tiene iguales valores de la solución), que a su vez se
resuelve fácilmente por "sustitución inversa"; un
procedimiento
simple que se ilustrará con la presentación
siguiente.
El esquema de Gauss empieza reduciendo un conjunto de
ecuaciones simultáneas, tal como se muestra en (2),
a un sistema triangular equivalente como:
Para ver la fórmula
seleccione la opción "Descargar" del menú
superior
(6)
en el cual los superíndices indican los nuevos
coeficientes que se forman en el proceso de reducción.
La reducción real se logra de la siguiente
manera:
Para ver la fórmula
seleccione la opción "Descargar" del menú
superior(7)
- La primera ecuación (2) se divide entre el
coeficiente de X1 en esa ecuación para
obtener:Para ver la fórmula
seleccione la opción "Descargar" del menú
superior(8)
- La ec. (7) se multiplica entonces por el coeficiente
de X1 de la segunda ecuación (2) y la
ecuación que resulta se resta de la misma, eliminando
así X1. La ec. (7) se multiplica entonces por
el coeficiente de X1 de la tercera ecuación
(2), y la ecuación resultante se resta de la misma para
eliminar X1 de esa ecuación. En forma similar,
X1 se elimina de todas las ecuaciones del conjunto excepto la
primera, de manera que el conjunto adopta la forma: - La ecuación utilizada para eliminar las
incógnitas en las ecuaciones que la siguen se denomina
Ecuación Pivote. En la ecuación
pivote, el coeficiente de la incógnita que se va a
eliminar de las ecuaciones que la siguen se denomina el
Coeficiente Pivote (a11 en los pasos
previos).Esta reducción nos conduce a:
Para ver la fórmula
seleccione la opción "Descargar" del menú
superior(9)A continuación se utiliza la tercer
ecuación (9) como ecuación pivote, y se usa el
procedimiento descrito para eliminar X3 de todas las
ecuaciones que siguen a la tercer ecuación (9). Este
procedimiento, utilizando diferentes ecuaciones pivote, se
continúa hasta que el conjunto original de ecuaciones
ha sido reducido a un conjunto triangular tal como se muestra
en la ec. (6). - Siguiendo los pasos anteriores, la segunda
ecuación (8) se convierte en la ecuación
pivote, y los pasos de la parte 1 se repiten para eliminar
X2 de todas las ecuaciones que siguen a esta
ecuación pivote. - Una vez obtenido el conjunto triangular de
ecuaciones, la última ecuación de este conjunto
equivalente suministra directamente el valor de Xn
(ver ec. 6). Este valor se sustituye entonces en la
antepenúltima ecuación del conjunto triangular
para obtener un valor de Xn-1, que a su vez se utiliza
junto con el valor de Xn en la penúltima
ecuación del conjunto triangular para obtener un valor
Xn-2 y asi sucesivamente. Este es el procedimiento de
sustitución inversa al que nos referimos
previamente.
Para ilustrar el método con un conjunto
numérico, apliquemos estos procedimientos
a la solución del siguiente sistema de
ecuaciones:
X1 + 4 X2 + X3 = 7
X1 + 6 X2 – X3 = 13 (10)
2 X1 – X2 + 2 X3 = 5
Utilizando como ecuación pivote la primera
ecuación (el coeficiente pivote es unitario),
obtenemos:
X1 + 4 X2 + X3 = 7
2 X2 – 2 X3 = 6 (11)
9 X2 + (0) X3 = -9
A continuación, utilizando la segunda
ecuación del sistema (11) como ecuación pivote
y repitiendo el procedimiento, se obtiene el siguiente
sistema triangular de ecuaciones:
X1 + 4 X2 + X3 = 7
2 X2 – 2 X3 = 6 (12)
– 9 X3 = 18
Finalmente mediante sustitución inversa,
comenzando con la última de las ecs. (12) se obtienen
los siguientes valores:
X3 = -2
X2 = 1
X1 = 5
Este método, que constituye una
variación del método de eliminación de
Gauss, permite resolver hasta 15 o 20 ecuaciones
simultáneas, con 8 o 10 dígitos significativos
en las operaciones aritméticas de la
computadora. Este procedimiento se distingue del
método Gaussiano en que cuando se elimina una
incógnita, se elimina de todas las ecuaciones
restantes, es decir, las que preceden a la ecuación
pivote así como de las que la siguen.El método se ilustra mejor con un ejemplo.
Resolvamos el siguiente conjunto de ecuaciones3.0 X1 – 0.1 X2 – 0.2 X3 = 7.8500
0.1 X1 + 7.0 X2 – 0.3 X3 = – 19.3
0.3 X1 – 0.2 X2 + 10 X3 = 71.4000
Primero expresemos los coeficientes y el vector de
términos independientes como una matriz
aumentada.Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del menú
superiorSe normaliza el primer renglón dividiendo
entre 3 para obtener:Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorEl término X1 se puede eliminar del
segundo renglón restando 0.1 veces el primero
del segundo renglón. De una manera similar, restando
0.3 veces el primero del tercer renglón se
elimina el término con X1 del tercer
renglón.Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorEn seguida, se normaliza el segundo renglón
dividiendo entre 7.00333:Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorReduciendo los términos en X2 de la
primera y la tercera ecuación se obtiene:Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorEl tercer renglón se normaliza dividiendolo
entre 10.010:Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorFinalmente, los términos con X3 se
pueden reducir de la primera y segunda ecuación para
obtener:Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorNótese que no se necesita sustitución
hacia atrás para obtener la
solución.Las ventajas y desventajas de la eliminación
gaussiana se aplican también al método de
Gauss-Jordan.Aunque los métodos de Gauss-Jordan y
de eliminación de Gauss pueden parecer casi
idénticos, el primero requiere aproximadamente 50%
menos operaciones. Por lo tanto, la eliminación
gaussiana es el mé todo simple por excelencia en la
obtención de soluciones exactas a las ecuaciones
lineales simultáneas. Una de las principales razones
para incluir el método de Gauss-Jordan, es la de
proporcionar un método directo para obtener la matriz
inversa.Para ver el item completo seleccione
la opción ¨Descargar trabajo¨ del menú
superiorEJEMPLO
Invertir la matriz
Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorAuméntese la matriz de coeficientes con una
matriz identidadPara ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorUsando a11 como pivote, el renglón 1
se normaliza y se usa para eliminar a X1 de los
otros renglones.Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorEn seguida, se usa a22 como pivote y
X2 se elimina de los otros renglones.Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorFinalmente, se usa a33 como pivote y
X3 se elimina de los renglones restantes:Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorPor lo tanto, la inversa es:
Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiorSe puede resolver un sistema de ecuaciones con la
inversa de la matriz de coeficientes, de la siguiente
manera:Para ver la fórmula
seleccione la opción ¨Descargar trabajo¨ del
menú superiordonde C es el vector de
términos independientes.Comparando ambos métodos, es evidente que el
método de inversión de matrices no es
práctico para la solución de un sólo
conjunto (o dos o tres conjuntos) de ecuaciones
simultáneas, porque la cantidad de cálculos que
intervienen para determinar la matriz inversa es muy grande.
Sin embargo, si se desea resolver 20 conjuntos de 10
ecuaciones simultáneas que difieren únicamente
en sus términos independientes, una matriz aumentada
que contiene 20 columnas de constantes (que se
utilizarían en el método de eliminación)
sería difícil de reducir, y se podría
usar con ventaja el método de inversión de
matrices.- MÉTODO DE GAUSS – JORDAN

- MÉTODO DE
GAUSS-SEIDEL
El método de eliminación para resolver
ecuaciones simultáneas suministra soluciones
suficientemente precisas hasta para 15 o 20 ecuaciones. El
número exacto depende de las ecuaciones de que se trate,
del número de dígitos que se conservan en el
resultado de las operaciones aritméticas, y del
procedimiento de redondeo. Utilizando ecuaciones de error, el
número de ecuaciones que se pueden manejar se puede
incrementar considerablemente a más de 15 o 20, pero
este método también es impráctico cuando
se presentan, por ejemplo, cientos de ecuaciones que se deben
resolver simultáneamente. El método de
inversión de matrices tiene limitaciones similares
cuando se trabaja con números muy grandes de ecuaciones
simultáneas.
Sin embargo, existen varias técnicas que se
pueden utilizar, para resolver grandes números de
ecuaciones simultáneas. Una de las técnicas
más útiles es el método de
Gauss-Seidel. Ninguno de los procedimientos alternos es
totalmente satisfactorio, y el método de Gauss-Seidel
tiene la desventaja de que no siempre converge a una
solución o de que a veces converge muy lentamente. Sin
embargo, este método convergirá siempre a una
solución cuando la magnitud del coeficiente de una
incógnita diferente en cada ecuación del
conjunto, sea suficientemente dominante con respecto a las
magnitudes de los otros coeficientes de esa
ecuación.
Es difícil definir el margen mínimo por
el que ese coeficiente debe dominar a los otros para asegurar
la convergencia y es aún más difícil
predecir la velocidad de
la convergencia para alguna combinación de valores de
los coeficientes cuando esa convergencia existe. No obstante,
cuando el valor absoluto del coeficiente dominante para una
incógnita diferente para cada ecuación es mayor
que la suma de los valores
absolutos de los otros coeficientes de esa ecuación, la
convergencia está asegurada. Ese conjunto de ecuaciones
simultáneas lineales se conoce como sistema
diagonal.
Un sistema diagonal es condición suficiente
para asegurar la convergencia pero no es condición
necesaria. Afortunadamente, las ecuaciones simultáneas
lineales que se derivan de muchos problemas de
ingeniería, son del tipo en el cual
existen siempre coeficientes dominantes.
La secuencia de pasos que constituyen el método
de Gauss-Seidel es la siguiente:
- Asignar un valor inicial a cada incógnita que
aparezca en el conjunto. Si es posible hacer una hipótesis razonable de éstos
valores, hacerla. Si no, se pueden asignar valores
seleccionados arbitrariamente. Los
valores iniciales utilizados no afectarán la
convergencia como tal, pero afectarán el número
de iteraciones requeridas para dicha convergencia. - Partiendo de la primera ecuación, determinar
un nuevo valor para la incógnita que tiene el
coeficiente más grande en esa ecuación,
utilizando para las otras incógnitas los valores
supuestos. - Pasar a la segunda ecuación y determinar en
ella el valor de la incógnita que tiene el coeficiente
más grande en esa ecuación, utilizando el valor
calculado para la incógnita del paso 2 y los valores
supuestos para las incógnitas restantes. - Continuar con las ecuaciones restantes, determinando
siempre el valor calculado de la incógnita que tiene el
coeficniente más grande en cada ecuación
particular, y utilizando siempre los últimos valores
calculados para las otras incógnitas de la
ecuación. (Durante la primera iteración, se deben
utilizar los valores supuestos para las incógnitas hasta
que se obtenga un valor calculado). Cuando la ecuación
final ha sido resuelta, proporcionando un valor para la
única incógnita, se dice que se ha completado una
iteración. - Continuar iterando hasta que el valor de cada
incógnita, determinado en una iteración
particular, difiera del valor obtenido en la iteración
previa, en una cantidad menor que cierto (*)seleccionado arbitrariamente. El
procedimiento queda entonces completo.
Refiriéndonos al paso 5, mientras menor sea la
magnitud del (*)seleccionado, mayor será la
precisión de la solución. Sin embargo, la
magnitud del epsilon no especifica el error que puede
existir en los valores obtenidos para las incógnitas, ya
que ésta es una función
de la velocidad de convergencia. Mientras mayor sea la
velocidad de convergencia, mayor será la
precisión obtenida en los valores de las
incógnitas para un (*)dado.
(*) Para ver la fórmula
seleccione la opción "Descargar" del menú
superior
EJEMPLO
Resolver el siguiente sistema de ecuación por
el método Gauss-Seidel utilizando un (*)= 0.001.
0.1 X1 + 7.0 X2 – 0.3 X3 = -19.30
3.0 X1 – 0.1 X2 – 0.2 X3 = 7.85
0.3 X1 – 0.2 X2 – 10.0 X3 = 71.40
SOLUCIÓN:
Primero ordenamos las ecuaciones, de modo que en la
diagonal principal esten los coeficientes mayores para asegurar
la convergencia.
3.0 X1 – 0.1 X2 – 0.2 X3 = 7.85
0.1 X1 + 7.0 X2 – 0.3 X3 = -19.30
0.3 X1 – 0.2 X2 – 10.0 X3 = 71.40
Despejamos cada una de las variables sobre la
diagonal:
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Suponemos los valores iniciales X2 = 0 y
X3 = 0 y calculamos X1
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Este valor junto con el de X3 se puede
utilizar para obtener X2
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
La primera iteración se completa sustituyendo
los valores de X1 y X2 calculados
obteniendo:
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
En la segunda iteración, se repite el mismo
procedimiento:
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Comparando los valores calculados entre la primera y
la segunda iteración
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Como podemos observar, no se cumple la
condición
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Entonces tomamos los valores calculados en la
última iteración y se toman como supuestos para
la siguiente iteración. Se repite entonces el
proceso:
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Comparando de nuevo los valores obtenidos
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Como se observa todavía no se cumple la
condición
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Así que hacemos otra
iteración
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Comparando los valores obtenidos
Para ver la fórmula seleccione
la opción ¨Descargar trabajo¨ del menú
superior
Dado que se cumple la condición, el resultado
es:
X1 = 3.0
X2 = -2.5
X3 = 7.0
Como se puede comprobar no se tiene un número
exacto de iteraciones para encontrar una solución. En
este ejemplo, se hicieron 3 iteraciones, pero a menudo se
necesitan más iteraciones.
a) ECUACIONES LINEALES
HOMOGENEAS
ECUACIONES LINEALES HOMOGENEAS DE PRIMER
ORDEN Consideramos la ecuación
![]()
y supongamos que ![]()
Podemos resolver directamente esta
ecuación:
Será ![]() …………………De la misma forma,
…………………De la misma forma,
tendremos
![]() , . . . .
, . . . .
Vemos que la solución general es
![]()
Llamamos a esta sucesión progresión
geométrica de valor inicial C y razón
A.
ECUACIONES LINEALES HOMOGENEAS DE SEGUNDO
ORDEN
• Partimos de la ecuación de
recurrencia
![]()
y buscamos soluciones que sean progresiones
geométricas:
Suponemos ![]() y sustituimos
y sustituimos
![]()
• Podemos simplificar esta ecuación en
la forma
![]()
de donde, si ![]() , deducimos
, deducimos ![]()
Llamamos a esta ultima ecuación la
ecuación característica de la
recurrencia.
Tenemos ahora tres casos:
1. Las raíces de la ecuación
característica son reales y distintas
Sean ![]() las raíces.
las raíces.
![]() son, para valores arbitrarios de las
son, para valores arbitrarios de las
constantes Ci, soluciones de la ecuación de
recurrencia (1). Comprobarlo sustituyendo.
• La suma de las dos soluciones anteriores
también es una solución. Lo comprobamos
sustituyendo.
• Hemos obtenido una solución que
depende de dos constantes arbitrarias.
Todas las soluciones están comprendidas en la
fórmula:
![]()
Demostración:
Si suponemos dados los valores iniciales,
a0 y a1, de la solución, el
resto de la sucesión queda unívocamente
determinado, por recurrencia y por ser la ecuación de
orden 2, por estos dos valores (igual que en el caso de
Fibonacci).
Sustituyendo n = 0, 1 en (2) obtenemos
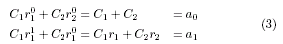
Como suponemos que a0, a1,
r1 y r2 son conocidos, vemos que (3) es
un sistema lineal de dos ecuaciones con dos
incógnitas.
Su determinante es ![]() y, por tanto, el sistema tiene
y, por tanto, el sistema tiene
solución única.
Hemos visto, entonces, que toda solución de
(1) puede ser dada como caso particular de (2) para una
elección adecuada, la dada por la solución de
(3), de las constantes C1 y
C2.
2. Las raíces de la ecuación
característica son reales e iguales Llamemos
r0 a la única raíz de la
ecuación característica.
La discusión es en este caso similar a la
anterior, salvo que debemos usar
![]()
Las comprobaciones necesarias para ver que, en este
caso también, todo funciona bien son tan parecidas que
las omitimos.
3. Las raíces de la ecuación
característica son números complejos
conjugados
Supongamos que las raíces son:
![]()
Podemos tratar este caso en la misma forma que el
primero, de forma que obtenemos que la solución
es
![]()
Esta solución es satisfactoria, salvo si
observamos que la solución está expresada en
términos de funciones de
variable compleja.
Si escribimos las raíces en forma polar,
![]()
![]() , donde podemos
, donde podemos
tomar como definición ei_ :
![]()
![]() podemos reescribir la solución
podemos reescribir la solución
como
![]()
con ![]() . De esta forma la solución es combinación
. De esta forma la solución es combinación
lineal de dos funciones de variable real y son los
coeficientes los que son números complejos.
Ejemplo:
Volvemos a la ecuación de Fibonacci ![]()
Su ecuación característica es
![]() , con
, con
raíces ![]() y
y
![]() . Son raíces reales
. Son raíces reales
distintas.
La solución general es
![]()
Sustituyendo n = 0, 1 en esta expresión
podemos obtener los valores de las constantes que
corresponden a valores iniciales dados. Por ejemplo,
para
F0 = 0 y F1 = 1 se obtiene
![]() .
.
¿Que valor tiene, aproximadamente,
Fn para n grande?
Como 0 < r2 < 1, para n muy grande el segundo
sumando de la expresión exacta obtenida para
Fn tiende a cero (i.e. se puede hacer tan
pequeño como queramos). Entonces, para n muy grande,
se obtiene
![]() .
.
ECUACIONES HOMOGÉNEAS DE ORDEN
ARBITRARIO
Consideramos la ecuación de recurrencia de
orden k
![]()
con ecuación característica, obtenida
en la misma forma que para k – 2,
![]()
Supongamos, para simplificar que la ecuación
característica tiene k raíces reales, r1, r2, .
. . , rk, distintas o no. Podemos entonces escribir la
ecuación característica en la forma ![]()
Teorema La solución general de la
ecuación de recurrencia (8) es una combinación
lineal de términos de la forma:
![]()
con ni – 1 términos por cada
raíz ri.
La resolución de ecuaciones no
homogéneas es, en general, bastante más
difícil que para el caso homogéneo.
Empezamos con un resultado general, y, luego, veremos
un método que, en
ocasiones, funciona.
Suponemos una ecuación no
homogénea
![]()
y llamamos ecuación homogénea asociada
a
![]()
Supongamos que conocemos una solución,
![]() ,de la
,de la
ecuación no homogénea
(9), a la que llamamos solución
particular.
Teorema Toda solución de (9) se puede escribir
como suma de la solución particular y una
solución cualquiera de la ecuación
homogénea asociada (10).
Demostración:
1. Representemos por an una solución
cualquiera de la ecuación (10). Si sustituimos ![]() en (9) vemos que se
en (9) vemos que se
satisface la ecuación.
2. Recíprocamente, supongamos que ![]() es otra solución
es otra solución
de (9). Restando y
sustituyendo en (10) vemos que ![]() es
es
solución.
Entonces, para resolver una ecuación, lineal,
no homogénea basta encontrar
una solución particular y resolver
completamente la ecuación homogénea
asociada.
Describo ahora, usando un ejemplo como ilustración, un método para
encontrar soluciones particulares.
Supongamos que la ecuación a resolver
es
![]()
1. Escribir la ecuación característica
de la ecuación homogénea asociada
y resolverla. Denotamos por p(r) el polinomio
obtenido.
En nuestro ejemplo, la ecuación
característica tiene raíces r = -3 y r =
2.
2. Encontrar la ecuación de recurrencia,
homogénea con coeficientes constantes, más simple
de la cual g(n) es solución.
Puede ser que g(n) no sea solución de ninguna
ecuación de recurrencia lineal, homogénea y con
coeficientes constantes.
Si es solución de una tal ecuación,
continuamos el procedimiento encontrando su ecuación
característica y resolviéndola. Denotamos por
q(r) el polinomio hallado.
En nuestro ejemplo, g(n) = 2n – 1, y una
ecuación de la que g(n) es solución tiene como
raíces 2 y 1.
El polinomio característico es (r-2)(r- 1) =
r2 – 3r + 2 =: q(r).
De aquí podemos obtener fácilmente la
ecuación de recurrencia, pero, realmente, no hace
falta.
3. Consideramos el polinomio P(r) := p(r)q(r), y
escribimos la solución general de una ecuación
homogénea con ecuación característica P(r)
= 0.
En el ejemplo, será:
P(r) : = p(r)q(r) = (r + 3) (r –
2)2 (r – 1)
y la solución asociada es:
H(n) : = A(-3)n +
B2n + Cn2n + D.
4. Los dos primeros sumandos de H(n) son la
solución general de la ecuación homogénea
asociada. Podemos ver que el resto es, para valores
particulares de las constantes, la solución particular
buscada.
En nuestro caso, la solución particular
sería
![]()
para valores de C y D que hay que calcular.
Sustituimos esta sucesión en (11), y operando,
llegamos a la ecuación
![]()
con solución D = 1/4 y C = 2/5.
Hemos comprobado así, que para estos valores de
C y D, se obtiene una
solución particular de la ecuación no
homogénea.
Ejercicio:
Usar el método anterior para hallar, para k =
2, 3, . . . , el valor de sumas del
tipo:
![]() .
.
Indicación:
Tenemos
![]()
que es una ecuación de recurrencia lineal, de
orden uno y no homogénea.
c) ANALISIS INSUMO-PRODUCTOS
ESTATICO NTERSECTORIALES
El análisis de insumo producto describe el
flujo de la producción para estudiar en que forma la
producción de bienes
primarios, intermedios y finales es afectada por un cambio en la
demanda de
bienes finales. El objetivo
primario del análisis de insumo-productos es evaluar los
niveles de producción en las diversas industrias,
que se requieren para niveles particulares de la demanda de
bienes finales. El análisis insumo-producto
también se puede aplicar al estudio de los sectores de
la economía, bien sea para un modelo
cerrad, en donde la producción de un sector es igual a
la adición de sus insumos en los otros sectores, o para
un modelo abierto, que incluye la demanda final además
de las demandas de los otros sectores.
Supóngase que una economía se divide en
n industrias, y cada industria
produce solamente un tipo de producto final. Usualmente las
industrias están relacionadas en el sentido de que cada
una de ellas debe usar algunos de los productos de las otras
para poder
funcionar. Ademas, una economia debe producir generalmente
algunos productos terminados para la demanda final. El
análisis de insumo-producto determina la
producción de cada una de las industrias si cambia la
demanda final, suponiendo que la estructura
de la economia no varia.
Es conveniente tabular los datos para el
análisis de insumo-producto, como se muestra en la tabla
8,
TABLA 8.1
| Usuario |
|
| ||
Productor | 1 2 …. | Demanda final | Producción | ||
1 | b1 1b1 2 | h 1 | x 1 | ||
2 | b2 1b2 2 | h 2 | x 2 | ||
. . . | . . . | . . . | . . . | . . . | . . . |
n | bn1bn 2 | h n | x n | ||
En donde bij es el importe (en unidades
monetarias) de los productos de la industria i empleados por la
industria j,hi es la demanda final para los
productos de la industria i y xi =
![]() es la
es la
producción total de la industria i.
La estructura de la economía se puede describir
ahora mediante la matriz tecnológica.
A= (aij)
En donde aij =
(bij/kj) = es el valor
monetario de la producción de la industria i que la
industria j debe adquirir para producir una unidad monetaria de
sus propios productos. Obsérvese que esta
definición de aij supone que la
adquisición de productos intermedios de una industria
son proporcionales al nivel de la producción de la
industria. Ente supuesto de proporcionalidad constante entre
insumos y productos es común en el análisis de
insumo-producto.
La i-ésima industria debe producir
![]() para i= 1,2,…, n
para i= 1,2,…, n
a fin de satisfacer las necesidades de todas las
industrias. El vector demanda interindustrial puede plantearse
entonces como AX, en donde
A=  y X =
y X = ![]()
La producción de la economía debe
ajustarse para satisfacer tanto las necesidades
Inter-industriales como la demanda final. Si el vector demanda
final es
H = ![]() hi ³ 0 i= 1,2 …, n
hi ³ 0 i= 1,2 …, n
Esta condición se puede describir
como
X= AX + H
Así;
[
I – A ]
X = H
y
X = [ I – A ] -1
H
La matriz I – a se conoce
como matriz de leontief.
Hay varios problemas matemáticos y
prácticos relacionados con el análisis del
insumo-producto. Por ejemplo, la matriz tecnológica debe
ser tal que cada una de las xi no sea
negativa; de lo contrario, la solución no tendrá
significado económico. También hay problemas que
conciernen a la clasificación de industrias y a la
estabilidad de la matriz tecnológica.
Dado un conjunto de demandas finales positivas,
considérese el problema de determinación de las
condiciones en las cuales existe un conjunto único de
niveles de producción positivos, compatible con el
conjunto de demandas finales. En primer lugar, como
[ I – A
] -1 debe
existir = [ I – A ] debe ser diferente de cero. Y cada elemento
de = [
I – A ]
-1 debe ser no negativo, pues de lo contrario
un incremento en la demanda final resultaría en un
decremento en la producción en algún punto del
proceso de producción. Se puede demostrar que, a fin de
que los niveles positivos de producción bruta
estén asociados a cualquier conjunto dado de demandas
positivas, se requieren las siguientes condiciones.
1 >
aij ³
0 para toda i y toda j
½ I –
A½
>
0
puesto que cualquier subconjunto de k
industrias de las n consideradas debe ser capaz de satisfacer
las demandas Inter-industriales con algún excedente para
satisfacer las demandas externas a las k industrias,
todos los menores principales del determinante de Leontief para
las n industrias
½
I – A½ = 
Deben ser positivos
Ejemplos
A
Considérense una economía
hipotética muy sencilla de dos industrias, A y B
representadas en la tabla 8.2
Tabla 8.2
| Usuario |
|
|
Productor | A B | Demanda final | Producción |
A | 500 350 | 150 | 1000 |
B | 320 360 | 120 | 800 |
En donde las cifras corresponden a
millones de unidades monetarias.
Determinar el valor producción de tal
economía si la demanda final cambia a 200 en el caso de
A y a 100, en el caso de B.
A= ![]()
I – A = 
[ I –
A ]
-1 ![]()

NOTA: [
I – A ]
![]()
Como debe ser el caso,
X = [ I – A ] -1 H ![]()
![]()
![]()
Y si H = ![]() , entonces
, entonces
X = [ I – A ] -1 H ![]()

![]()
Es decir, la industria A debe tener una
producción de 1138 ![]() y la industria B debe tener una
y la industria B debe tener una
producción de 844![]() , en donde los valores de producción
, en donde los valores de producción
están dados en millones de unidades monetarias de
productos.
B.
Considérese una economía
hipotética muy simple de tres industrias A, B y C, cuyas
características están representadas en la tabla
8.3,
Tabla 8.3
| Usuario |
|
|
Productor | A B C | Demanda final | Producción |
1 | 90 150 225 | 75 | 540 |
2 | 135 150 300 | 15 | 600 |
3 | 270 200 300 | 130 | 900 |
y las cifras indican millones de unidades monetarias
de productos.
Obtener el vector producción correspondiente a
dicha economía si la demanda final cambia a:
(a) 50 para A, 10 para B y 100 para C.
(b) 100 para A, 20 para B y 60 para C.
(c) 80 para A, 100 para B y 120 para C.
A= 
[ I
– A ] = 
[ I –
A ]
-1 ![]()

NOTA: |
I – A | ![]()
![]()





como debe ser el caso
 (a) si
(a) si 
 (b) si
(b) si 
d) LA CONDICIÓN DE
HAWKING-SIMON
Dada una economía ficticia con tres sectores
productivos, cuya matriz de intercambios intersectoriales
(matriz de transacciones) es:
Para ver la fórmula seleccione
la opción "Descargar" del menú
superior
- Construir la tabla input/output completa para un
vector de producción
x=(120,150,200)t. - Sin calcularla, analizar si la matriz inversa de
leontief es no negativa. - Hallar, sin calcular la matriz inversa de leontief,
la producción total necesaria en cada sector para
alcanzar un vector de demanda final d=(78,21,128)T.
1º.- PLANTEAMIENTO INICIAL:
usaremos en este ejercicio las ecuaciones del modelo
input-output de Leontief, aunque no podamos calcular la
matriz inversa.
2º.- APARTADO A: a partir
de los intercambios intersectoriales y el vector de
producción (outputs totales), calcularemos tanto la
demanda final como los inputs primarios, sin más que
tener en cuenta que el modelo de Leontief establece que, para
cada sector, los inputs totales coinciden con los outputs
totales.
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
3º.- APARTADO B:
para analizar la existencia de la matriz inversa de
Leontief y si ésta es no negativa, usaremos la
condición de Hawking-Simon, que dice que
existe (I-A)-1³ 0 si y
sólo si I-A
cumple la condición de Hawking-Simon, esto es,
si todos sus menores principales son positivos.
El primer paso debe ser calcular la matriz de
coeficientes técnicos, para lo cual dividimos cada
intercambio sectorial entre el input total
correspondiente a su sector. Después
calcularemos I-A
y calcularemos sus menores.
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
Por tanto, I-A cumple la condición de
Hawking-Simon, por lo que sabemos que existe la matriz
inversa de Leontief y es no negativa. Esto quiere decir que
la economía ficticia dada por nuestra matriz de
intercambios es productiva.
4º.- APARTADO C: para
hallar la producción sin calcular la inversa de
Leontief, plantearemos las ecuaciones del modelo y
resolveremos el sistema de ecuaciones
correspondiente:
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
Se despejan las demás incógnitas,
quedando finalmente el vector de producción
como:
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
e) PRODUCTOS Y PRECIOS
TEORIA Y APLICACIONES
PRODUCTO
DEFINICIÓN:
El producto es el bien o servicio a
ofrecer, surge de la utilización de materias primas
(materiales o
intelectuales) para formar un útil, que
puede generar un consumo que
pueda ser comprado o que tenga un valor para quien lo
disfrute.
à
Nos referimos tanto a los bienes tangibles como a
servicios
intangibles.
à
Es un haz de atributos percibidos físicos
químicos y / o tangibles que tienen el potencial de
satisfacer las necesidades de los clientes
presentes y potenciales.
El producto tiene un significado para el que lo vende,
para los clientes meta y para la sociedad.
La organización de los productos ven a un
producto desde la perspectiva de la
organización: como una manifestación de los
recursos
utilizados para producirlo. Las organizaciones
de la mercadotecnia ven a un producto desde la
perspectiva del cliente meta.
Como perciben, sus clientes meta el producto es un mayor
interés; no los recursos utilizados para
lograr el producto. Estas organizaciones descubren que el
producto es un vehículo principal de la organizaciones
para entregar las satisfacciones del cliente y que no hay
necesidad de distribuir, promover y poner precio a un
producto que no ofrezca beneficios al cliente, porque el
producto no se venderla.
La clave para entender el concepto es
verlo desde la perspectiva del cliente meta: como un haz de
satisfacciones.
La opinión de la sociedad hacia el producto a
veces choca con la del cliente meta o del mercado
tecnólogo, o con ambas. Por ejemplo: el equipo de
seguridad
que se requiere en los autos es a
veces criticado por clientes y vendedores.
Las consideraciones sociales se están volviendo
mas importante en las decisiones del producto, en especial en
las áreas de seguridad y empaque.
DISEÑO DEL PRODUCTO:
El primer paso en el diseño del producto es identificar el
mercadeo meta y
recopilar información acerca de sus
características y de sus expectativas del
producto.
Los beneficios que quieren los clientes potenciales
son una consideración fundamental con el diseño
del producto.
Por lo general los productos son funciones
múltiples tienen un mercado mas amplio que los de una
sola función. Pero si un comprador potencial cree que un
producto es capaz de hacer demasiado funciones, puede sospechar
que ninguna de ellas las hace bien. Un producto es un conjunto
de satisfacciones debido a sus características: calidad,
estilo, ejecución y materiales.
Cada uno influye en la imagen del
producto. Mas calidad de la que espera el cliente meta puede
hacer que el precio del producto este fuera de su
alcance.
El estilo (color, aroma,
tamaño, etc) es importante para productos desde papel
sanitario hasta mobiliario para oficinas. Los
diseñadores de productos esta poniendo cada vez mas
énfasis al lado humano del diseño de sus
productos: la ingeniera de los factores humanos, o ergonomía.
Los clientes también esperan un cierto nivel de
ejecución del producto, en las décadas de 1950 y
1960 los fabricantes de autos participaron en una carrera de
caballos de fuerza
cuando se dieron cuenta de que la gente querían autos de
ejecución superior.
Los materiales que se utilizan para elaborar un
producto pueden ser muy importantes. Las decisiones en la
selección del material pueden afectar en
el atractivo de ventas de su
producto y no deben tomarlos únicamente los gerentes de
producción, escasez de
materiales en algunas industrias y cuestiones concernientes a
la seguridad y la salud pueden conducir al
as empresas a
buscar alternativas. También las consideraciones del
costo pueden
ser un factor.
El diseño del producto también debe
incluir los beneficios que esperan los intermediarios. Aunque
los clientes finales están en primer lugar, no deben
pasarse por alto que los intermediarios.
Los científicos clasifican a las plantas y
animales
similares en grupos para
estudiarlos. Los comerciantes clasifican bienes y servicios en
grupos para desarrollar generalizaciones acerca de mezclas de
mercadotecnia deseables para los distintos grupos. Por
ejemplos, podemos dividir el producto en tres clases basados en
la durabilidad.
- Bienes no durables; se consume en uno o en uno
muy limitado números de usos. - Bienes durables; un bien durable dura para
muchos usos. - Servicios; los bienes tangibles, son
actividades, beneficios o satisfacciones intangibles que se
ofrecen a la venta debido
a la creciente importancia de los servicios en nuestra
economía, se decidió, dividir los productos
(bienes tangibles y servicios intangibles) en dos grandes
clases: de consumo e industriales.
Los productos de consumo se compran para satisfacer
necesidades personales y domesticas. Los productos industriales
se compran para utilizarse en la producción de otras
productos de consumo o industriales para utilizarse en la
producción de otros productos en consumo o industriales
o para utilizarse en la conducción de las operaciones de
una organización.
CLASIFICACIONES DE LOS PRODUCTOS DE
CONSUMO
Existen muchas bases para clasificar los bienes de
consumo, la mas usada es de comportamiento del comprador.
Este sistema de clasificaciones se basa en la
diferencias del comportamiento de compra de la gente que
adquiere los productos en st. Por lo tanto, cualquier producto
puede clasificarse de manera diferente dependiendo del
comportamiento del comprador. Este sistema obtiene resultados
por el comportamiento de los consumidores, ya que su
comportamiento es semejante para comprar un determinado
producto. Existen cuatro clases de productos de consumo y
son:
- Productos de conveniencia
- Productos de comparación
- Productos de especialidad
- Producto no solicitados
- Productos de conveniencia: son todos aquellos
atributos o servicio de bajo precio que compran los
consumidores con un mínimo de esfuerzo de compra. Con el
esfuerzo para conseguir estos productos es mínimo, los
encontramos al alcance de muchos mercados.
Estos productos se subclasifican en la siguiente
manera:
- productos principales
- productos por impulso
- producto de urgencia
Dentro de los ejemplos de producto principales para
muchos consumidores están el pan, la leche y el
transporte
por autobús o por tren subterráneo. Estos
productos se adquieren regular y rutinariamente.
Las compras de
los productos por impulso no se planean en absolutos. La
exposición del producto incita a
quererlo. El deseo de compra productos principales pueden
forzarlo a ir de compras. El deseo de comprar productos por
impulso es un resultado de su compra. Es por eso que los
productos por impulso se localizan en donde se puede
ver.
Las compras de productos de urgencia son un resultado
de las necesidades urgentes y precisas. Un ejemplo de productos
de urgencia son los servicios de ambulancia y primeros
auxilios.
Los consumidores consideran que los productos de
comparación heterogénea son diferentes o no
regidos por la misma norma. Compran por lo mejor
comparación de precios y calidad. El precio suele ser
secundario al estilo y la calidad cuando son difíciles
de hacer las comparaciones de precio. otros ejemplos de
productos de comparación heterogéneo para
muchos consumidores son las niñeras y
enfermeras.- Producto de comparación: implican
confrontaciones de precio y calidad. Los productos de
comparación puede ser homogéneos o
heterogéneos. Los consumidores consideran que los
productos de comparación homogéneos son
parecidos.Los compradores se desviaron de un camino para
localizar y comprar estos productos de especialidad debido a
su conocida calidad y otros beneficios.La mayoría de los servicios al consumidores
que involucran un alto grado de experiencia están
considerados como producto de especialidad y sus productos
mediante frases publicitarias como " no acepte imitaciones",
"exija lo verdadero y "vale la pena el viaje desde cualquier
parte". Ellos crean lealtad en los consumidores cuando estos
consideran que sus marcas son
productos de especialidad. - Producto de especialidad: los bienes o
servicios para las que el comprador tiene enormes convicciones,
como la marca, el
estilo o el tipo. Además un esfuerzo especial para
comprarlos. - Producto no solicitado: son los productos que
los compradores no saben que existen o que no quieren pensar en
su compra. Existen dos tipos, los productos no solicitados
comunes y los productos no solicitados nuevos. Estos son
productos existentes que los consumidores no quieren pensar en
comprarlos, aunque con el tiempo
pueden adquirirlo.
Los productos que son totalmente nuevos y desconocidos
a los consumidores son productos no solicitados
nuevos
CLASIFICACIONES DE LOS PRODUCTOS
INDUSTRIALES.
se puede clasificarse dentro de dos categorías,
dependiendo del uso que se le den. la primera categoría,
productos sobrantes, incluye aquellos que serán parte
del producto para cuya elaboración se
utilizaran.
- Materia prima
- Partes componentes
- Materiales.
La segunda categoría, productos de apoyo
incluye aquellos que se necesitaran para conducir las
operaciones de la organización:
- Instalaciones
- Equipo accesorio
- Suministros
- Servicios comerciales
Materia prima: Los productos que solo se han
sometido a un proceso para permitir su manejo conveniente y
económico. Hay dos subclases que son productos del campo
(como el tabaco, el
trigo, y la soya) y los productos naturales (como los productos
mineros, forestales y marinos).
La materia
prima es un artículo de gastos porque
su costo se paga en el año que se compra. Los
procedimientos de compra dependen del suministro actual y
anticipado del mercado, precio y porcentaje del costo total de
producción del producto terminado que se debe a la
materia
prima.
Los problemas del suministro también conducen a
menudo o que los usuarios busquen nuevos fuentes y
materiales sustitutos.
La materia prima es a veces voluminosas, baja del
valor y se encuentra en lugares muy alejados de donde se
necesita.
Es por eso que el costo del transporte es muy
importante en su esfuerzo por mantener estos costos bajos,
algunas empresas tiene su propio equipo de
transporte.
Partes y materiales componentes: Son los
productos que ya están listos para su ensamblaje directo
en el producto terminado, o bien, que requieren de solo un
proceso posterior menor.
Los materiales componentes: Requieren de un
proceso posterior antes de llegar a ser parte del producto
terminado.
Las partes y materiales componentes se convierten en
parte del producto terminado y son artículos de
gastos.
Instalaciones: Son subclases de las
instalaciones, son el terreno, los derechos e tierras,
plantes y las edificaciones.
Las siguientes discusiones se enfoca en las
consideraciones del producto en compañía de
producto múltiple. Tales empresas venden mas de un
producto mas satisfacer los deseos de sus clientes
meta.
La mezcla de productos de una empresa
incluye todos los productos que ofrece.
Una mezcla de producto tienen las dimensiones
estructurales de extensión (o amplitud) y profundidad.
La extensión se refiere al numero de las diferentes
líneas de productos
La profundidad se refiere al numero de
artículos de productos.
1 INTRODUCCIÓN
Precios, en Economía, valor de
mercado de los bienes, medido en términos de lo que un
comprador está dispuesto a dar para obtenerlos.
Normalmente, los precios se expresan en función de una
cantidad de dinero
—de hecho, la principal razón por la que se
utiliza el dinero
reside en su utilidad para
reflejar el valor de los precios—, pero en los sistemas
de trueque los precios vienen dados por el valor de un bien en
relación con otros bienes que, a su vez, tienen un
determinado valor, por lo que todos los precios de todos los
bienes se determinan mutuamente sin que intervenga el dinero.
Los precios son el principal mecanismo de ajuste de la oferta y la
demanda, ya que el precio de cualquier bien, en una
economía de libre mercado, tiene que alcanzar el punto
donde se equilibre la producción y el consumo: este
precio de equilibrio
refleja el punto donde concuerda lo que los productores pueden
costear y lo que los consumidores están dispuestos a
pagar. Por lo tanto, los precios determinarán qué
y cuánto se produce, cómo se produce y
quién puede comprarlo. Son un aspecto crucial en
la ciencia
económica, especialmente en microeconomía.
2 DETERMINACIÓN DE LOS PRECIOS MEDIANTE LA
OFERTA Y DEMANDA
Tanto los factores de oferta como los
de demanda determinan los precios de los bienes: los precios
disminuirán si hay exceso de oferta y aumentarán
si la demanda es excesiva, hasta que se alcance el equilibrio.
Del lado de la oferta, los precios vienen dados por los costes
de producción y distribución, que a su vez están
determinados por la escasez de materia prima, la tecnología y las limitaciones de tipo
organizativo: la ley de los
rendimientos decrecientes, los costes laborales,
etcétera. El productor determinará su estrategia de
precios con el fin de maximizar sus beneficios, aunque
también puede tener otros objetivos,
como los contemplados en la teoría de la empresa. Sin
embargo, la determinación de los precios también
depende del tipo de mercado: en un monopolio o
en un oligopolio
los precios se pueden aumentar porque no hay competencia. En
un cártel las empresas pueden fijar el precio si hay
acuerdo entre ellas; la estrategia a largo plazo de una
empresa
puede requerir que se establezcan precios inferiores a los del
mercado e incluso inferiores a los costes; la teoría de
juegos puede influir en las decisiones de las empresas. En
la práctica, son pocos los mercados perfectamente
competitivos y son habitualmente los productores los que salen
beneficiados.
La demanda es la suma de las
decisiones independientes de los consumidores de un mercado que
pretenden maximizar su utilidad. Este precepto asume, por
supuesto, que los consumidores realizan elecciones racionales:
éstas son precisamente las que se intentan modificar
mediante la publicidad y el
marketing.
La información de los consumidores suele ser escasa, lo
que rompe el modelo ideal. Los costes que deben pagar los
productores para alterar el sentido de la demanda pueden
afectar a los precios, al repercutir en ellos los costes de
promoción del producto. Los consumidores
decidirán comprar un producto en función de su
precio, pero realmente lo que determina la demanda efectiva es
la cantidad de bienes vendidos a un determinado precio y no el
precio de venta, ya que las empresas preferirán crear un
nuevo producto antes que dejar que el precio del producto
conocido caiga hasta su nivel de equilibrio. Por otra parte, el
que los precios sean bajos no tiene por qué ser un
factor positivo: los bienes de calidad no se venderán
con bajos precios porque los consumidores pensarán que
son defectuosos o porque perderán su
característica de exclusividad, que, de hecho, es la
esencia de su utilidad. En muchos modelos de
economías de libre mercado se considera que el precio al
que se compra un bien se establece mediante una negociación, pero esto ocurre pocas veces
en las modernas economías integradas, por lo que la
relación entre precio y demanda no es tan directa como
la que se deriva de la teoría
económica.
3 CONTROL DE
PRECIOS E INFLACIÓN
Los gobiernos siempre han querido influir en
la determinación de los precios por varias razones. En
las economías planificadas, los precios los fija
el Estado,
por lo que las fuerzas del mercado no influyen en absoluto en
la determinación del precio. El fracaso de las
economías planificadas modernas refleja la eficiencia de
los precios como mecanismo de ajuste económico; sin
embargo, suele ser habitual que los estados intervengan en el
proceso de fijación de precios, aunque en menor grado.
En algunos casos, esta intervención intentará
elevar el nivel de precios, como en el caso de la Política Agraria
Común de la Unión
Europea (UE), mediante la cual los países elevan los
precios de los productos agrícolas comprando los
excedentes para proteger a los agricultores de la UE. En otros
casos, se intervendrá el mercado para mantener los
precios bajos, como en el de las concesiones públicas
después de su privatización, limitándose los
beneficios de la empresa de servicios
públicos para evitar que exploten el monopolio
efectivo del que disponen. Además, los gobiernos pueden
querer subvencionar mediante subsidios determinadas empresas y
mantener así sus precios a bajos niveles, o
también pueden establecer aranceles
sobre las importaciones,
aumentando el precio de los bienes extranjeros. También
se pueden congelar los precios durante una guerra para
paliar los efectos económicos de la escasez.
El control de precios por parte del
Estado suele
ser parte de un conjunto de medidas de políticas de rentas y precios cuyo fin es
controlar la inflación, que consiste en el persistente
aumento del nivel de precios, lo que no implica un cambio en el
valor de los bienes, sino más bien en el valor del
dinero. Esto refleja el hecho de que el dinero es en sí
mismo un bien con su propio precio, en función del valor
de otros bienes, y por lo tanto su precio puede caer si su
oferta es excesiva (argumento principal del monetarismo). Si la demanda es superior a la
oferta, los precios deberían subir, pero si un Gobierno
está manteniendo artificialmente los precios por debajo
de su nivel de equilibrio, no habrá inflación a
pesar del exceso de demanda, lo que acarreará escasez,
racionamiento, la aparición del mercado negro y otras
deficiencias típicas de las economías
planificadas. Si la unidad monetaria de un país no tiene
una demanda suficiente en los mercados de divisas, la
inflación podrá aumentar puesto que el precio de
esa unidad monetaria, en términos de las demás,
caerá, lo que hará aumentar el precio de sus
importaciones y disminuir el de sus bienes de exportación, con lo que caerá la
actividad exportadora.
En economía existen muchas ideas
y sistemas, como la doctrina económica marxista, que
consideran que existe un precio justo ideal, determinado por
una ley natural a la que se llega por mecanismos distintos a
los de la oferta y la demanda. En la práctica, el
mecanismo de los precios ha dado excelentes resultados cuando
se ha dejado que actúe libremente, pero sus efectos han
sido mediocres cuando se ha intentado variar los precios en
función de intereses altruistas o
egoístas.
ESTRATEGIAS DE FIJACIÓN DE
PRECIOS
- DIFERENCIACIÓN POR
COSTOS: La
rentabilidad
a largo plazo de una empresa depende en gran medida de una
política de precios adecuada. Si el precio es demasiado
bajo, en comparación con el costo, el volumen de
ventas puede ser grande, pero los beneficios inapreciables o
nulos. Uno de los factores de éxito
y perdurabilidad de una empresa radica en la eficacia de la
fijación de los precios. Un producto constituye una base
económica viable para edificar y sostener una empresa en
tanto y en cuanto dicho producto o servicio encuentre mercados
y sea fuente de rentabilidad a un determinado nivel de precios.
Estratégicamente, la función de precio es la de
promover un acuerdo de retorno sobre la
inversión. - COMPETENCIA: El
precio del producto viene, muchas veces, impuesto por
la situación de la competencia, pues muchas empresas
fabrican productos prácticamente iguales. En estos
casos, se forma un precio en el mercado que no permite
modificaciones. La fijación de un precio superior
conduciría a los consumidores hacia los productos de
la competidores. Las empresas del mismo sector es frecuente
que realicen acuerdos de precios entre ellos para evitar
entrar en una guerra de precios, porque es perjudicial para
ambas empresas en el largo plazo, no es una estrategia con
resultados muy claros. Cuando una empresa se encuentra en
situación de Líder, el resto de las empresas del
sector de actividad se ven obligadas a fijar sus precios casi
simultáneamente a los del líder. Por lo tanto
el grado de diferenciación de un producto respecto de
la competencia, determina en gran manera las limitaciones a
que está sujeta una empresa para fijar sus precios.
Esta diferenciación puede lograrse de distintas
maneras: por diseño del producto, por su apariencia,
por su imagen de marca, por la reputación de la
empresa o por su disponibilidad en el mercado, siempre que la
misma sea apreciada por los consumidores.Podemos diferenciar: precio Psicológico
(equilibrio entre calidad-precio), precio máximo que
está dispuesto a pagar y el precio mínimo al
que no compraría el producto porque pensaría
que no es de buena calidad.El conocimiento de los precios por los
consumidores.
– Hay muy pocos productos cuyo precio es conocido con
exactitud por los consumidores.
– No hay diferencia en el
conocimiento del precio en función del sexo, edad
o nivel de venta.
El precio es un elemento de información con mucho
peso en el proceso de decisión de compra.
– Si el consumidor
carece de otras informaciones relativas al producto, el
precio será el factor predominante.
– Cuando la información referente a otras
características del producto aumenta, la importancia
del precio disminuye.
La relación precio-calidad: se han hecho
diferentes experiencias realizadas con dos lotes iguales de
naranjas poniéndoles diferentes precios. Las
más caras se venden mejor. A un mayor precio, se
asocia la idea de mejor calidad.
La imagen de marca juega un papel esencial.La empresa debe mostrarse sensible a las variaciones
de los hábitos de compra y a la aceptación por
parte de los clientes por sus precios. Debe esforzarse por no
fijar precios exagerados, ya que de esta manera puede limitar
el número de unidades vendidas. Pero al mismo tiempo
se debe tener en cuenta los costos y el margen de
utilidad. - CONSUMIDOR: Es
importante no olvidarnos de un factor esencial, lo que el
cliente está dispuesto a pagar por el producto "factor
de percepción". - PROPUESTA SELLADA
(Kotler) Licitaciones.
ESTRATEGIA DE FIJACIÓN D
PRECIOS POR MEZCLA DE PRODUCTOS
- FIJACIÓN DE PRECIOS POR
LÍNEA DE PRODUCTOS
Las empresas normalmente desarrollan líneas de
productos e introducen niveles de precios. Diferencias de
calidad que justifiquen las diferencias de precios de un mismo
producto. Eje Fiat 147 de mayor calidad y precio y Fiat Vivace
modelo económico.
- FIJACIÓN DE PRECIOS POR
PRODUCTOS OPCIONALES
Muchas empresas ofrecen productos,
características y servicios opcionales junto con el
producto principal.
Eje. Diario Clarín, opcional enciclopedias.
Otro ejemplo son los autos que se pueden optar por
múltiples accesorios como levanta vidrios
eléctricos, llantas, aire
acondicionado, mayor garantía, etc.
- FIJACIÓN DE PRECIOS POR
PRODUCTOS CAUTIVOS
Algunos productos requieren el uso de productos
auxiliares o cautivos. Ejemplo las impresoras
se comercializan a bajo precio y añaden sobreprecios a
los cartuchos. Otro ejemplo Maquina de afeitar Mach 3 y los
repuestos a altos precios.
- FIJACIÓN DE PRECIOS EN DOS
PARTES
Las empresas de servicios a menudo practican la
fijación de precios en dos partes, que consiste en una
cuota fija más una cuota variable por consumo. Ejemplo:
las empresas de telefonía.
- FIJACIÓN DE PRECIOS DE
SUBPRODUCTOS
La producción de ciertos bienes a menudo genera
subproductos.
- FIJACIÓN DE PRECIOS POR
CONJUNTO DE PRODUCTO
Quienes venden a menudo agrupan sus productos y
características y les ponen precio fijo. Eje
McDonald’s ofrece un Combo a un precio menor de lo que
costaría comprar los productos
individualmente.
ESTRATEGIA DE AJUSTE DE PRECIO
- FIJACIÓN
GEOGRÁFICA (efectivo, comercio a
cambio, trueque)
Implica que la empresa decida la fijación de
sus precios en cuanto a poner sus productos en los diferentes
lugares y países. Política de precios
geográficos: el precio debe estar determinado por la
decisión de incluir o no los gastos de flete, otra
cuestión es cómo recibir el pago.
- DESCUENTOS Y
BONIFICACIONES
Pronto Pago: Descuento en
efectivo, es una reducción de precios para los que pagan
sus facturas oportunamente.
Cantidad: por grandes volúmenes. Eje $10
x U en menos de 100 unidades y $ 9 x U en más de 100
unidades.
Temporada: Un descuento por temporada es una
relación de precio que se hace a los compradores que
adquieren Eje rebajas en hoteles en temporada baja de
turismo.
Descuentos funcionales o comerciales:
disminuciones en el precio a miembros del canal comercial por
realizar distintas funciones de venta, almacenaje o contabilidad.
Complementos: pagos extras, programas
especiales para revendedores.
Complementos a cambio: Descuentos de precio a
quienes entregan algo a cambio. Eje autos plan
canje.
Complementos promociónales: son pagos o
reducciones de precios que recompensan a los comerciantes que
participan en los programas de publicidad y apoyo de
ventas.
- FIJACIÓN
DISCRIMINATIVA
Por segmento de Clientes: se
cobran diferentes precios por el mismo producto o servicio a
deferentes grupos de clientes. Por ejemplo es común que
los museos cobren una cuota de admisión màs baja
a estudiantes o jubilados. Damas gratis en algunos lugares
bailables.
Por la forma de producto: Diferentes versiones
del producto llevan diferente precio pero no en
proporción a sus respectivos costos.
Por la imagen: Algunas empresas ponen al mismo
producto precios en dos niveles distintos con base en
diferencias de imagen.
Por el Lugar: El mismo producto tiene diferente
precio en diferentes lugares aunque el costo de ofrecerlo en
ambos lugares sea el mismo Eje. Platea-Popular, fila 1 a 10 en
teatros, asientos en aviones en primera categoría o
segunda.
Por el tiempo: Los precios varían por
temporada, día u hora. Ejemplo los miércoles el
cine es
más barato, el teléfono tiene diferentes tarifas en hora
pico o sábado, domingo o feriados.
- FIJACIÓN
PSICOLÓGICA
Los precios psicológicos tienen la finalidad de
estimular las compras que se basan mas bien en reacciones
emotivas que en reacciones racionales. La teoría de
fijación de precios impares supone que se
venderán más unidades de un producto si su precio
se fija en 99.90 que en 100. Un segundo enfoque se basa en
la atracción misma de los números.
Se piensa que ciertos números tienen más
atractivos físicos para la gente. En esta forma el
número ocho tan simétrico será más
atrayente que un 7 o un 4 que son números con puntas y
bordes muy marcados. Fijación de precios según
la costumbre, es el caso en el cual los precios de algunos
productos se fijan de acuerdo a la tradición.
- FIJACIÓN PROMOCIONAL
para estimular las compras tempranas, a corto
plazo.
Fijación de precios carnada con
pérdidas: Supermercados para estimular el
tráfico.
Fijación de precio por evento
especial:
Devoluciones en efectivo
Financiamiento con intereses bajos
Plazos más largos para pagar
Garantías y contrato de
servicio.
Matemáticas para la
administración y economía, WEBER JEAN
E.
http://www.luda.uam.mx
http://www.matebrunca.com
http://www.ejerciciosresueltos.com
Omar Neira

