- Conceptos
básicos - Voltaje y corriente como
funciones de la posición - Acoplamiento de las
líneas de transmisión - Potencia
- Carta de
Smith
Las ondas planas
uniformes, son ejemplos de propagación de ondas sin
guías (libremente), en el sentido de que una vez que se
han propagado en una dirección, dentro de un bloque infinito de
material, continúan propagándose en la misma
dirección. De acuerdo con lo anterior, las líneas
de transmisión (al igual que las guías de onda) se
utilizan para guiar la propagación de la energía de
un punto a otro.
Así pues,
una línea de transmisión se puede definir como un
dispositivo para transmitir o guiar energía de un punto a
otro. Usualmente se desea que la energía sea transportada
con un máximo de eficiencia,
haciendo las pérdidas por calor o por
radiación
lo más pequeñas posible.
Las líneas de
transmisión pueden ser de muchas formas y tamaños.
Es conveniente clasificarlas en base a las configuraciones de sus
campo E y H, es decir, en base a los modos que pueden transmitir.
De esta manera, las líneas de transmisión se pueden
dividir en dos grupos
principales:
1) Las que son capaces de transmitir el modo Transversal
Electromagnético (TEM). Del cual se desprenden las
O.P.U.
2) Las que son capaces de transmitir
únicamente modos de orden más alto.
En un modo TEM ambos, el
campo
eléctrico y el campo
magnético, están completamente en la
dirección de propagación. No hay componente ni de
E, ni de H en la dirección de transmisión. Por
ejemplo, si la dirección de transmisión es en Z,
entonces las únicas posibilidades para la dirección
de E y de H serían Ex y Hy ó
Ey y Hx. La única diferencia con las
O.P.U. es que en el modo TEM E y H no necesariamente son
independientes de su posición en el plano formado por XY
(el cual es transversal a Z). Mientras que en las O.P.U. E Y H
sí deben ser independientes de su posición en estos
planos (esto es la característica de
uniformidad).
Los modos de más alto
orden siempre tienen al menos una componente, de alguno de los
campos en la dirección de transmisión.
Todas las líneas de dos
conductores como el cable coaxial
o el cable de dos hilos son ejemplos de líneas que
transmiten el modo TEM o simplemente de líneas TEM;
mientras que las guías de onda huecas, de un solo
conductor, son ejemplos de líneas de modos más
altos.
En resumen:
1) Línea modo TEM.- E y H son totalmente
transversales a la dirección de
transmisión. Ejemplos: todas las líneas de
dos conductores.
2) Línea modo de más alto orden.- E
ó H ó ambos tienen componentes en la
dirección de transmisión. Ejemplos de modos
de más alto orden son el modo TM,
el modo TE. Ejemplos de este tipo de líneas de
transmisión son las guías de onda
huecas de un solo conductor o las líneas
trifásicas.
En el ámbito electrónico el término
"línea" o "línea de transmisión" usualmente
se utiliza únicamente para hacer referencia a los
dispositivos que pueden transmitir modo TEM, mientras que el
término "guía" o "guía de onda" se utiliza
para hacer referencia a los dispositivos que pueden transmitir
modos de más alto orden.
A continuación se
muestra el
diagrama
(figura 1.1) utilizado para representar una línea de
transmisión y en seguida se mostrarán algunas
analogías útiles entre las O.P.U. y las
líneas de transmisión:
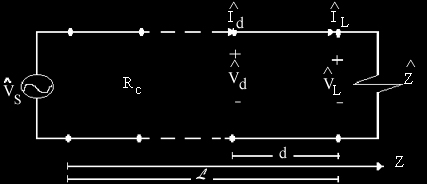
FIGURA 1.1
Donde
Para ver la fórmula seleccione
la opción "Descargar" del menú
superior
es el voltaje de entrada o voltaje de la fuente
de alimentación, Rc es la impedancia
intrínseca de la línea de transmisión y
sus unidades son ohms,
Para ver la fórmula seleccione
la opción "Descargar" del menú
superior
es la impedancia de carga y puede ser un número
complejo o un número real y sus unidades también
son ohms,
Para ver la fórmula seleccione
la opción "Descargar" del menú
superior
es el voltaje en la carga,
Para ver la fórmula seleccione
la opción "Descargar" del menú
superior
es la corriente que pasa por la carga, L es la
longitud de la línea de transmisión en metros y
se mide sobre el eje Z, d es la distancia de un punto
determinado a la carga en metros, las otras dos variables
serán definidas en la siguiente sección en base a
la distancia d.
Las analogías entre las
O.P.U. y las líneas de transmisión son las
siguientes:
O.P.U. | Líneas de |
| Ê |
|
|
Rc | W |
VOLTAJE Y
CORRIENTE COMO FUNCIONES DE LA
POSICION
Las formas de onda del voltaje
y la corriente en la línea de transmisión son la
combinación de ondas que se desplazan hacia adelante y
hacia atrás. Estas se combinan para producir ondas
estacionarias en la línea, de manera análoga a
como se observó en el estudio de la incidencia de ondas
planas uniformes en fronteras planas. Para mostrar la existencia
de ondas estacionarías en la línea, vamos a
escribir las expresiones para voltaje y corriente en la
línea, en términos de un voltaje de
carga
(Z=L)=
(L)=
y una corriente de carga
( Z = L ) =
( L) =
, a estas dos variables las definimos
como:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.1a)
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.1b)
El coeficiente de reflexión en un punto
particular de Z se define como la razón de los
voltajes:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.2)
También definimos una
impedancia de entrada a la línea en cualquier punto a lo
largo de ella como la razón del voltaje total a la
corriente total:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.3)
Donde:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.4a)
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.4b)
Substituyendo (1.4) en
(1.3):
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Si, L es la distancia de la entrada a la carga (la
longitud de la línea de transmisión), entonces
podemos encontrar una impedancia en la carga
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.6)
Donde
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
es el coeficiente de reflexión en la
carga
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
y se define de la siguiente manera (ecuación
1.1):
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.7)
El cual en términos de
la impedancia de carga es:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.8)
Se puede demostrar
que:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.9)
Si en (1.1) se
despeja
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
y se substituye en (1.4) junto con
(1.9):
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
Volts
(1.10a)
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Amperes
(1.10b)
Nótese que estos
resultados involucran la distancia a la carga, la cual
definimos como L-Z. Así, si definimos d = L-Z, las
ecuaciones
en (1.10) quedan de la siguiente manera:
Para ver la fórmula seleccione la opción
"Descargar" del menú superior
Volts
(1.11a)
Para ver la fórmula seleccione la opción
"Descargar" del menú superior
Amperes
(1.11b)
Donde
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
e son los fasores de voltaje y corriente,
respectivamente, a una distancia d.
El análisis de las variaciones de las
magnitudes del voltaje y la corriente a una distancia d de la
carga es muy útil y se realiza a continuación,
antes de eso es necesario obtener la magnitud de
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
, a partir de las ecuaciones (1.11):
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
(1.12a)
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
(1.12b)
Nótese que la influencia de d (la distancia)
está contemplada en los términos
. Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
Hay varios casos de
consideración especial:
1.- La carga en corto circuito,
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
= 0: Para este caso,
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
=-1 el voltaje de carga
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
es cero. La ecuación para la corriente de carga
en (1.12b) se vuelve:
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
=
(1.13)
Para obtener la
ecuación (1.13) se utilizó la igualdad
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
. Como
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
= 0, no es apropiado utilizar la ecuación
(1.12a) para analizar la magnitud del voltaje a lo largo de la
línea de transmisión, así que la
ecuación a utilizar es :
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Volts
(1.14)
La magnitud de
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
queda de la siguiente manera :
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
Volts
(1.15)
Substituyendo
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
= 1 en (1.15) tenemos :
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
=
(1.16)
De la carga, como se muestra en la figura
1.1.
De esta manera, la magnitud del voltaje a lo largo de
la línea de transmisión varía con el seno
de la distancia eléctrica de la carga. Nótese que
un mínimo y un máximo adyacentes están
separados por a l
/ 4. De manera similar, los máximos
adyacentes y los mínimos adyacentes están
separados por l
/ 2. Por ejemplo, Si ocurre un máximo en
d1 y un mínimo en d2, estos puntos
deben estar separados por:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.17)
Resultados similares se
aplican a la corriente máxima y mínima
respectivamente. Más adelante veremos que esto es un
resultado general sin importar la impedancia de
carga.
2.- La carga en circuito abierto,
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
= ¥
: Para este caso,
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
= +1 y la corriente en la carga
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
es cero. La ecuación para el voltaje de carga
en (1.12a) se vuelve:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.18)
En este caso, la
ecuación (1.12b) no es correcta para analizar la
corriente a lo largo de la línea de transmisión,
así que es necesario utilizar la siguiente forma
:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.19)
Nótese que otra vez,
un máximo y un mínimo adyacentes están
separados por l
/ 4. Tanto los máximos adyacentes como los
mínimos adyacentes están separados por
l /
2.
Nótese también
que una línea que tenga una longitud de un cuarto
de l y que
termine en un circuito abierto aparecería como un corto
circuito. A una distancia de un cuarto de longitud de onda
(l ),
el voltaje se va a cero, mientras que la corriente no, esto
indicaría que se trata de un corto circuito.
Observaciones similares se aplican al caso de una línea
que tenga una longitud de un cuarto de lambda
(l /
4) y que termine en un corto circuito, a una distancia de un
cuarto de longitud de onda de la carga (d = l / 4), la corriente es
cero, mientras que el voltaje no, esto indicaría que se
trata de un circuito abierto.
3.-Carga resistiva, è RL: En el caso de alguna
carga resistiva
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
es real, así que
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
y el coeficiente de reflexión en la
carga es un número real, es decir,
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
. Para este caso los mínimos o máximos
del voltaje y de la corriente van a ocurrir exactamente en la
carga. Para RL>Rc es positivo y en la carga
ocurrirá un máximo de voltaje y un mínimo
de corriente. Para RL<Rc es negativo y
las propiedades antes mencionadas se invierten, es decir, en la
carga ocurrirá un máximo de corriente y un
mínimo de voltaje. Nótese que estas propiedades
se confirman para cargas en circuito abierto y en corto
circuito respectivamente.
Finalmente, si RL
= Rc se dice que la línea está
acoplada, es el caso óptimo y el que generalmente se
desea que ocurra. Para esta caso
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
= 0 y no hay variación en la magnitud
del voltaje ni en la magnitud de la corriente a lo largo
de la línea.
4.- Carga compleja caso general,
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
: Para una carga reactiva general
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
los resultados antes mencionados no cambian, con una
sola excepción : Para esta carga
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
y esto da como resultado un coeficiente de
reflexión en la carga complejo, lo cual ocasiona que ni
los máximos, ni los mínimos de voltaje y de
corriente ocurran en la carga. Excepto por esta diferencia se
tienen las siguientes propiedades generales:
(a) Un máximo y un mínimo, en la magnitud,
de voltaje (o corriente) están separados por
l /
4.
(b) Los puntos correspondientes en la magnitud del
voltaje (y la corriente), en sus formas de onda, se
repiten entre distancias separadas por múltiplos de
l / 2.
(c) El voltaje y corriente total (magnitud y fase) se
repiten entre distancias separadas por múltiplos
de l
.
ACOPLAMIENTO DE
LAS LÍNEAS DE TRANSMISIÓN:
Como se mencionó en el
capítulo anterior, el caso ideal u óptimo es tener
una línea de transmisión acoplada, esto significa
que RL = Rc. Cuando
RL&RC
se dice que la línea está desacoplada.
Siempre que sea posible se
desea acoplar las líneas de transmisión para
eliminar las reflexiones. Las líneas no acopladas (
RL&;
Rc ó = Rc ) ocasionan ecos
(reflexiones), como se discutió en la sección
anterior estas reflexiones dan lugar a las ondas estacionarias.
Esta situación puede ser particularmente indeseable, por
ejemplo, en los circuitos
telefónicos.
La técnica de
acoplamiento que se abordará en esta sección
será la de las secciones acopladoras (stub-tuner) o
espolones. La idea consiste básicamente en determinar el
valor de la
impedancia de alguna red auxiliar, la cual cuando
sea conectada a la línea de transmisión
provocará que = Rc. Como se puede ver el caso
más general es cuando la impedancia de carga es compleja y
debido a que la impedancia de la línea es puramente real,
entonces la impedancia de esta red auxiliar debe ser puramente
compleja (reactiva) y cuyo valor debe ser igual al de la parte
reactiva de la impedancia de carga.
La base de esta idea se explica
a continuación, en la figura 1.2. Se puede encontrar un
punto a lo largo de la línea de transmisión de tal
manera que la admitancia de entrada tenga una parte real igual a 1 /
Rc y alguna parte imaginaria X, es decir :
= ( 1 / Rc ) + j
X
(1.20)
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
FIGURA 1.2
Este hecho se puede ver
fácilmente si si notamos que la admitancia normalizada a
Rc de la ecuación (1.20) es:
=
Rc
= 1 +
j X
Rc
La siguiente pregunta que es necesario responder es
"¿Qué estructura
debe tener la red acopladora?". Como ya se ha mencionado antes,
es claro que esta red debe proveer una admitancia que sea
puramente reactiva (que no tenga parte real), la cual
podría ser capacitiva o inductiva puesto que X puede ser
positivo o negativo. La manera más obvia y más
simple de hacer esto es conectar en paralelo con la línea,
a la distancia adecuada, un capacitor o un inductor que tenga el
valor adecuado de admitancia. El problema que conlleva esta
solución es que este tipo de elementos no se comportan
como simples capacitores o
simples inductores cuando son operados a frecuencias cercanas al
rango de los Giga hertz. Abajo de este rango de frecuencias
sí serán adecuados para realizar el acoplamiento.
Cuando la línea va a operar en rangos de frecuencia
más altos para implementar la red acopladora se utiliza
una sección de línea de transmisión que
tenga las mismas características de ésta,
(impedancia intrínseca Rc constante de
fase b y
una longitud L ) y que esté cortocircuitada, es decir, que
termine en corto circuito. A este pedazo de línea se le
conoce como stub o stub-tuner. también se podrían
utilizar stubs con terminación en circuito abierto, pero
son más difíciles de construir y son poco
utilizados.

En la figura 1.3 se muestra el diagrama de una
línea de transmisión con un stub-tuner conectado a
ella.
FIGURA 1.3
Puesto que no siempre es
posible acoplar una línea exactamente, se desea tener una
medida del grado de desacoplamiento. Esta medida se llama
Razón de Voltaje de Onda Estacionaria (VSWR) y se define
como la razón de la magnitud del voltaje máximo en
la línea a la magnitud del mínimo voltaje en la
línea:
VSWR =
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
Nótese que en el caso acoplado la razón
del voltaje máximo al voltaje mínimo dentro de la
línea es igual a 1, es decir,
VSWR= 1 para =
RC
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.23)
y VSWR
=¥
para = 0 ó para
= ¥
(1.24)
De esta manera, la VSWR nos
da una medida del desacoplamiento de la línea.
Nótese que la VSWR siempre será un número
real positivo y que su valor va a estar entre 1e
¥
:
1 ≤ VSWR < ¥
(1.25)
Entre más cerca
esté la VSWR de la unidad, mejor acoplada está la
línea. Se puede determinar una fórmula para la VSWR
en términos de Rc y
. Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
(1.26a)
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
(1.26b)
Substituyendo las ecuaciones
de (1.26) en la definición de VSWR, ecuación
(1.22):
VSWR =
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
(1.27)
Debido a que la magnitud del
coeficiente de reflexión es constante en todos los
puntos a lo largo de la línea, entonces será
igual al inicio que en la carga:
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
Y (1.27) se puede escribir
como:
VSWR =
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
(1.28)
Por otro lado, si se conoce
la VSWR por mediciones o por algún otro medio, se puede
calcular la magnitud del coeficiente de reflexión en
cualquier punto de la línea utilizando la siguiente
ecuación:
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
=
(1.29)
Líneas de Transmisión con
pérdidas:
- Constante de propagación compleja (modo
cuasi-TEM):

Para pérdidas pequeñas,
![]()

- Constante de atenuación:
![]() ,
,![]() de
de
la línea sin pérdidas
Constante de fase:
![]()
Impedancia característica:

![]() para
para ![]()
Distorsión en líneas con
pérdidas.
– Las aproximaciones para y son para
pérdidas pequeñas.
– En general, ambas son dependientes de la
frecuencia:
– Para una señal no monocromática,
cada componente armónica sufrirá diferente
atenuación y viajará con distinta velocidad de
fase.
– Ello supone distorsión de la
señal.
– En el caso particular R/L=G /C, la l’nea está libre de
distorsión, aún teniendo
pérdidas.


La línea con pérdidas
terminada.
Las ondas de tensión y corriente
son:

Impedancia a lo largo de la línea:


El coeficiente de reflexión varía ahora
tanto en módulo como en fase


![]()

El flujo medio de potencia
es:

Las pérdidas en un tramo de longitud d de
la línea son:
![]()
Expresadas en dB:
![]()
O en nepers:
![]()
En la sección anterior
requerimos numerosas operaciones
algebraicas con números complejos (suma, resta,
multiplicación y división) para obtener ciertas
cantidades de interés.
La carta de
Smith es una ingeniosa técnica gráfica que
virtualmente evita todas estas tediosas operaciones con
números complejos. Por ejemplo, se puede determinar la
impedancia de entrada a una línea de transmisión
dad su longitud eléctrica y su impedancia de
carga.

Considérese la línea de transmisión
uniforme y sin pérdidas, con resistencia
característica Rc y constante de
fase b =
2p
/l
, como se ve en la figura 1.4. Como se
discutió en la sección anterior, la impedancia de
entrada a la línea en cualquier punto a lo largo de
ella, , se puede determinar de la siguiente
manera.
FIGURA 1.4
El coeficiente del voltaje de reflexión
G ( Z ) en cualquier punto Z en
la línea y la impedancia de entrada a la línea en
el mismo punto Z, , se relacionan por:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.30)
Y el coeficiente del voltaje de reflexión
en cualesquiera dos puntos de la línea, Z 1 y
Z 2, se relacionan por :
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.31)
Donde la constante de fase b está dada por:
b
=2p
/l
= w
/V (1.32)
donde V es la velocidad de propagación de la onda
dentro de la línea, asumiendo que el medio dentro de la
línea es homogéneo y está caracterizado por
las propiedades m
y e
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
, w
es la frecuencia de operación en radianes
y l
es la longitud de onda en el medio, en metros. Se cumple la
relación l =V / f, donde f es la frecuencia de
operación en Hertz.
La clave para entender la carta de Smith
(lo cual es importante para su efectivo y adecuado uso), radica
en el hecho de que la carta de Smith relaciona,
gráficamente, la impedancia de entrada (1.30) en
algún punto de la línea y el coeficiente del
voltaje de reflexión (1.31) en ese mismo punto. Lo primero
que se debe hacer es determinar la impedancia de entrada
normalizada a la impedancia de la línea Rc.
Para normalizar se realiza lo siguiente:
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
=r + j
x
(1.33b)
donde r y x son las partes real e imaginaria,
respectivamente, de
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
. De manera similar, el coeficiente de reflexión
en este punto se puede escribir en términos de su parte
real y su parte imaginaria p y q , respectivamente
:
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
= p +
jq
(1.34)
Substituyendo (1.34) en (1.33a) obtenemos:
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
(1.35)
Si igualamos (1.33b) con (1.35) :
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
(1.36)
Si se iguala la parte real del lado izquierdo con la
parte real del lado derecho en (1.36) y se iguala la parte
imaginaria del lado izquierdo con la parte imaginaria del lado
derecho en (1.36) y después se hace cierta
manipulación algebraica, se obtiene :
Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
Las ecuaciones (1.37) son las ecuaciones de dos
círculos. En particular, (1.37a) es la ecuación de
un círculo de radio y centrada en el
punto
. Para ver la
fórmula seleccione la opción "Descargar" del
menú superior
La ecuación (1.37b) es la ecuación de un
círculo de radio 1/X y centrada en el
punto
Para ver la fórmula seleccione la
opción "Descargar" del menú superior

FIGURA 1.5
La Carta de Smith se forma con la combinación
gráfica de estos dos círculos, representados por
las ecuaciones (1.37). El coeficiente de reflexión del
voltaje G
=p + jq se puede dibujar en el plano pq. La
ecuación (1.37a) da una relación entre la parte
real de
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
, entre r, p y q. La ecuación (1.37b) da la
relación entre la parte imaginaria de
Para ver la fórmula seleccione la
opción "Descargar" del menú superior
, entre x, p y q, como se muestra en la figura
1.5.
Si se grafican las dos ecuaciones para distintos
valores de r y
x, y después se superponen ambas gráficas, se obtiene la Carta de Smith
original (1949), la cual se muestra a continuación, en la
figura 1.6 Las líneas de x constante son
circunferencias de radio 1/x centradas en el punto [1,
1/x]. (líneas en azul). Figura 1.6B

FIGURA 1.6

Figura 1.6b
Para ver el gráfico seleccione la
opción "Descargar" del menú superior
FIGURA 1.6C. Familia de
circunferencias de radio 1/(r+1), centradas en
(r/(r+1),0)

FIGURA 1.6D. G Se representa en circunferencias
centradas en el origen de la carta.
El resultado importante es el hecho de
que el coeficiente de reflexión del voltaje y la
impedancia de entrada a la línea normalizada en el mismo
punto de la línea, están relacionados por la carta
de Smith (Fig. 1.6). En la parte exterior de la carta hay varias
escalas.
En la parte exterior de la carta está una
escala llamada
"ángulo del coeficiente de reflexión en grados", a
partir de ésta se puede obtener directamente el valor
de q G . Un par de escalas de suma
importancia son las que relacionan la longitud de la línea
de transmisión en l ´s el inicio de estas dos escalas
está en el lado izquierdo de la carta de Smith y una de
ellas corre en el sentido de las manecillas del reloj,
ésta se denomina "wavelengths toward generator"
(longitudes de onda hacia el generador), esto indica que si se
utiliza esta escala se estará avanzando hacia el
generador, hacia la entrada de la línea, en unidades
de l . La otra
escala corre en sentido contrario de las manecillas del reloj y
se denomina "wavelenghts toward load" (longitudes de onda hacia
la carga), esto indica que si se utiliza esta escala se
estará avanzando hacia la carga, hacia el final de la
línea, en unidades de l .
En el fondo de la carta hay un conjunto de varias
escalas, una de las cuales está denominada "Reflection
coeff. Vol" (Coeficiente de reflexión del voltaje). Si se
mide la longitud del vector, trazado siempre desde el origen, se
puede utilizar esta escala para conocer la magnitud del
coeficiente de reflexión del voltaje, G . El resto de las escalas deben
ser explicadas en la clase. El
punto importante es que la carta de Smith es una
relación gráfica entre la impedancia de entrada
normalizada y el coeficiente de reflexión del voltaje en
el mismo punto de la línea y utilizando la carta se pueden
evitar los laboriosos cálculos con números
complejos para conocer la impedancia de entrada a la línea
o el coeficiente de reflexión. Otras aplicaciones de la
carta de Smith son en el cálculo
del inverso de un número complejo, lo cual resulta muy
sencillo, y en el acoplamiento de las líneas de
transmisión.
Razón de onda estacionaria
(VSWR=S)
La razón de onda estacionaria también
puede representarse en la carta de Smith.
 y,
y,
puesto que la impedancia normalizada es:

Recordando que la tensión en la línea
es:
![]() en un
en un
máximo de tensión será
![]() y para
y para
la corriente

Así:

La razón de onda estacionaria coincide con el
máximo valor de r (está en el eje real
positivo)
Análogamente:

Que está en el punto diametralmente
opuesto.
Existe una escala adicional para la ROE, al pie de la
carta. (En VSWR y dB).
La carta de Smith. Otras propiedades.
En la carta de Smith, un número complejo se
invierte sin más que moverse al punto diametralmente
opuesto:
Dada una impedancia

un desplazamiento de l /4 (p radianes) hace ![]() con lo que:
con lo que:

Esto nos permite trabajar cómodamente con
impedancias y admitancias.
Acoplamiento:
Por acoplamiento entendemos establecer un coeficiente de
reflexión nulo en algún punto de la línea
(para lo cual debe existir alguna discontinuidad).
Por ejemplo: consideremos dos líneas de
impedancias características Z0 y Z1
conectadas en serie, siendo la segunda de ellas indefinida(o
terminada en su carga adaptada).

Los voltajes, referidos a la
discontinuidad:

con  como ya sabemos.
como ya sabemos.
Igualando los voltajes en z=0:

Para ver el gráfico seleccione la
opción "Descargar" del menú superior
FIGURA 1.7. Impedancia y admitancia en
la carta de Smith
El objetivo del
acoplamiento será, conseguir G =0- T= 1
La carta de Smith en líneas con
pérdidas.
– La principal diferencia con el caso sin
pérdidas es que el módulo del coeficiente de
reflexión no permanece constante
![]()
lo que hace que el lugar del coeficiente de
reflexión no sea una circunferencia sino una espiral
logarítmica.
- Se puede utilizar la carta de Smith si "reducimos" en
el factor al ir
al ir
hacia el generador, o "aumentamos" en el factor
al ir hacia la carga
Potencia
El flujo medio de potencia es:

Las pŽrdidas en un tramo de longitud
d de la l’nea son:
![]()
expresadas en dB:
![]()
o en nepers:
![]()
EJEMPLOS:
Ejemplo1
En un punto dado de la línea, se ha medido un
coeficiente de reflexión ![]()
Determinar la impedancia normalizada en ese
punto:
1. Localizamos el punto G con la ayuda de la escala.
2. Leemos los valores de
r y x
ZN= 0.32+j0.63
3.- El valor exacto es:
ZN= 0.30+j0.65
Para ver el gráfico seleccione la
opción "Descargar" del menú superior
FIGURA E-1
Ejemplo2
Dada una carga de valor ZN=2.4-j0.6 ,
encontrar el coeficiente de reflexión:
1.- Localizamos el punto de impedancia dada.
2.- Medimos su distancia al centro y lo trasladamos a la
escala del
Coeficiente de reflexión.
3.- Medimos el ángulo, a partir del punto
0¼
Obtenemos ![]()
4.- El valor teórico es:
![]()
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
FIGURA E-2
Ejemplo 3
Una línea de transmisión de 10 m. de
largo, con impedancia característica de
50W , trabajando
a una frecuencia, cuya longitud de onda es de 5.882 m. en la
línea, termina en una carga de (50+j100)W . Determinar la impedancia de
entrada.
1.- Localizamos ZLN=1+j2
2.- Expresamos la distancia en longitudes de
onda:
10m = 1.70 x 5.882m = 1.70l
3.- Nos movemos sobre la circunferencia que contiene a
ZLN en sentido horario
(Hacia el generador) 1.70l (Nótese que una vuelta completa es
0.5 l
)
4.- Determinamos el punto, obteniendo
ZinN=0.29-j0.82
5.- El valor de la impedancia es, por lo tanto
Zin=(14.5 – j41) W
Frente el valor exacto de Zin=(14.52 –
j40.52) W
De paso, los coeficientes de reflexión en la
carga y a la entrada, son:
![]()
Frente a los valores teóricos
![]()
Para ver el gráfico seleccione la
opción "Descargar" del menú superior
FIGURA E-3
Ejemplo4
Una línea de impedancia característica
Zo=100 W
termina en una carga ZL= (150 – j200)
W . Encontrar la ROE y
la distancia a la que la impedancia aparece como resistiva
pura.
1.- Normalizamos la impedancia: ZLN= (1.5 –
j2)
2.- La localizamos en la carta de Smith.
3.- Medimos su distancia al centro de la carta y la
trasladamos a la escala inferior VSWR. (Alternativamente, podemos
girar hasta el eje real positivo y medir el valor de
r)
S=4.5
4.- Medimos el giro (en longitudes de onda) hasta el
punto del eje real más próximo
d= 0.5 l
– 0.302 l
= 0.198 l
(hacia el generador)
Para ver el gráfico seleccione la
opción "Descargar" del menú superior
FIGURA E-4
La carta de Smith en líneas con
pérdidas.
Ejemplo:
Encontrar la impedancia de entrada en una línea
de 30.48 m, de impedancia característica
Zo=53.5 y terminada en una carga de
ZL=(100+j150) trabajando a una
=2m,
si las pédrdidas totales son de 4.5
dB.
1.- no dB=4.5 dB=8.686d
=1.70×10-2 dB/m
2.- Atenuaci—n
![]()
Ejemplo:
3.- Localizamos ZLN = 1.87 +
j2.80.
4.- Nos movemos hacia el generador 15.24
(0.24).
Encontramos ZN = 0.17 – j0.35.
5.- Reducimos el radio en un 35.5%
Encontramos ZinN = 0.62 – j0.21
Para ver el gráfico seleccione la
opción "Descargar" del menú superior
También se puede recurrir a la siguiente
dirección en la web, en donde se
encontrará información sobre líneas de
transmisión, Carta de Smith, archivos
descargables e incluso utilidades para trabajar con la Carta de
Smith:
http://wyndury.radionet.udg.mx/wyndury/comunicaciones/cables_modem/
http://mailweb.udlap.mx/~lgojeda/tutoriales/ie38001/submenu7.htm
http://mailweb.udlap.mx/~lgojeda/apuntes/electro/capitulo7/chapter7.htm
Para ver el gráfico seleccione la
opción "Descargar" del menú superior
Daniel Leopoldo González
Clarembaux