Elementos de geometría

Desarrollo del
contenido
Bibliografía

Los antiguos Egipcios dependían exclusivamente
de las aguas del río Nilo para efectuar sus trabajos
agrícolas. El Nilo se desbordaba año con
año, inundando grandes extensiones de tierra, la
cual quedaba así apta para los cultivos. En las riveras
del río se median y se distribuían las distintas
parcelas para ser asignadas a los agricultores.

Este proceso
debía repetirse año con año, pues cada
inundación borraba las medidas del año
anterior.

Así poco a poco, se fue perfeccionando la
técnica de parcelas y nació la Geometría, que etimológicamente
significa medición de tierras. Los Egipcios pues
crearon la Geometría
y la desarrollaron a tal grado que aun hoy tenemos como mudos
testigos de ese desarrollo a
las grandiosas pirámides de Egipto, cuya
antigüedad supera los 5,000 años.

Desarrollo de Contenido

ANGULOS

Cuando dos rectas se encuentran y forman cuatro religiones llamadas
ángulos. Cada ángulo esta limitado por dos
lados y un vértice.

Es la abertura entre dos lados, los cuales tienen un punto
común llamado vértice.

El lado desde el cual se empieza a medir el ángulo
se llama Codo Inicial, y aquel donde se termina se llama
Lado Terminal.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Tipos de Ángulos

Angulo Convexo: Se llama
ángulo convexo R N M a la intersección del
semiplano de borde NM, que contiene el punto R, y el semiplano de
borde NR, que contiene el punto N.

Angulo Cóncavo: Es el
ángulo que se obtiene si consideramos la unión de
los semiplanos anteriores.

Ángulos
Consecutivos: Son los pares de ángulos
que tienen un lado común y ningún otro punto
mas.

Ángulo Llano: Cuando los
lados de un ángulo son dos semirrectas de una misma recta,
el ángulo se llama llano.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

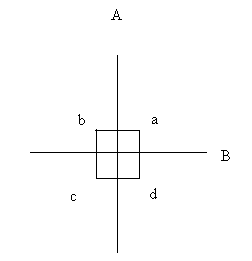
Ángulos Rectos: Sean dos
semirrectas de origen de un origen común O y
supongámoslas prolongadas hasta formar dos rectas, a y b,
que se cortan en O y que dividen al plano en 4 regiones a, b, c y
d, cada una de ellas correspondiente a un ángulo. Cuando
esos cuatro ángulos son iguales, se dice que cada uno de
ellos es un ángulo recto y que sus lados son
perpendiculares.

Angulos Oblicuos: Las rectas que se
cortan formando ángulos desiguales se llaman oblicuas. A
estos ángulos que no son rectos se les llaman
oblicuos.

Agudos: Si son menores que un
recto.
Obtusos: Si son mayores que un
recto.

MEDIDA DE ANGULOS

Para medir ángulos se emplean fundamentalmente
dos sistemas: el que
utiliza como unidad el grado sexagesimal y el que utiliza como
unidad el radián.

Medición de
ángulos

Medir un ángulo es compararlo con otro que se
toma por unidad de medida. Para medir los ángulos existen
varios sistemas, siendo los más conocidos el sistema
sexagesimal y el circular.

Sistemas de medidas
angulares

Sistema Sexagesimal: en éste sistema la
unidad de medida es el grado sexagesimal que corresponde a
que se abrevia 1°; éste a su
vez se divide en 60 partes iguales y corresponde a un minuto sexagesimal que se
abrevia ; éste a su vez se divide en 60
partes iguales y corresponde a un segundo sexagesimal que
se abrevia

. Para ver el gráfico seleccione
la opción "Descargar" del menú superior

Sistema Circular: en éste
sistema la unidad de medida es el radian.

¿Qué es el radian?: El radian es un
ángulo central que tiene como lados 2 radios de una
circunferencia, cuyo arco es igual al radio de la
circunferencia al cual pertenece.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Siendo;  = 3,141592654

R = 1

Las unidades de medida que pasaré a estudiar
pertenecen al sistema sexagesimal y circular.

Equivalencia entre los
sistemas

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Ángulos Complementarios: Son
los que miden 90º.

Ángulos Suplementarios: Son los que miden
180º

LONGITUD DE ARCO

Si ө es un ángulo
central que mide un radian entonces la longitud del arco
subtendido es igual al radio (r). Donde r es la longitud del
radio.

Cuando en ángulo Ө
mide 2 radianes, entonces la longitud del arco subtendido
mide 2 r.

De manera general si el ángulo mide + radianes
entonces la longitud de arco subtendido mide + r.

TRIÀNGULOS

Es la figura que consta de tres lados,
tres ángulos y tres vértices.

Clasificación de los Triángulos:

Por sus Lados

Triangulo Equilátero:

Si tiene sus tres lados iguales.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Triangulo Isósceles:

Si tiene dos lados iguales.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Triangulo Escaleno:

Si sus tres lados son desiguales.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Por sus Ángulos:

Triangulo Acutángulo:

Es el que tiene sus tres ángulos agudos.

Triangulo Rectángulo:

Es el que tiene un ángulo recto.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Triángulo Obtusángulo:

Es el que tiene un ángulo obtuso.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Los lados de un triangulo rectángulo reciben
nombres especiales:

Catetos: Son los dos lados que forman el
ángulo recto.

Hipotenusa: Es el lado opuesto al ángulo
recto.

Dos de los ángulos son, necesariamente, agudos.
El tercero puede ser también agudo, o bien recto u obtuso.
Si los tres ángulos son agudos el triángulo se
llama acutángulo, si tiene un ángulo recto,
rectángulo y obtusángulo si el mayor de sus
ángulos es obtuso.

Triángulos
Rectángulos

Los triángulos rectángulos
cumplen una serie de relaciones métricas importantes entre
sus lados.

Los lados de un triángulo
rectángulo que forman el ángulo recto, b y c, se
llaman catetos y el tercer lado, a (opuesto al ángulo
recto) es la hipotenusa. El teorema de Pitágoras relaciona
los dos catetos y la hipotenusa: en un triángulo
rectángulo, el cuadrado de la hipotenusa es igual a la
suma de los cuadrados de los catetos:
a2 = b2 + c2

Otra relación importante
que se cumple en un triángulo rectángulo es el
teorema del cateto: el cuadrado de cada cateto es igual al
producto de la
hipotenusa por su proyección sobre ella, es
decir,

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

c2 = a · m, b2 = a · n

TEOREMA RELATIVO A LA SUMA DE LOS
ANGULOS INTERNOS DE UN TRIÀNGULO

"La suma de las medidas de
los tres ángulos internos de un triángulo
cualquiera es siempre igual a 180º"

Dem. Grafiquemos un triángulo
cualquiera

Demostraremos que:

a + b +
c =
180º

Primeramente trazamos una recta paralela al
segmento

, como
se muestra a
continuación

Podemos observar que:

d + c + f = 180º

TEOREMA RELATIVO A LA SUMA DE LOS
ANGULOS EXTERNOS DE UN TRIANGULO

"La suma de las medidas de los 3
ángulos externos de un triangulo cualquiera siempre es
igual a 360º

Dem:

d + e + f = 360º

Obsérvese que:

d + a
= 180º Por ser

e + b
= 180º ángulos

f + c
= 180º suplementarios

SEMEJANZA DE TRIANGULOS

Relación entre dos figuras geométricas que
tienen la misma forma, aunque distinto tamaño. Entre los
elementos (puntos, rectas, ángulos,…) de esas dos
figuras se establece una relación por la que cada elemento
f le corresponde otro de f´

Dos figuras semejantes f y f´ cumplen con las
siguientes relaciones métricas:

Proporcionalidad de Segmentos: entre dos figuras
semejantes, los pares de segmentos correspondientes son
proporcionales. Si A, B, C son puntos de f y A’, B’,
C’ los correspondientes puntos de f entonces se cumple
que:

La razón de proporcionalidad K se
llama razón de semejanza. Por ejemplo, entre dos
figuras semejantes cuya razón de semejanza es 2, cada
segmento de la primera es de longitud doble que el
correspondiente segmento de la segunda.

Razón de dos Segmentos de Recta: Es el
cociente de sus longitudes.

Encontrar el valor de
X

Si y solo si 3X = 4(6)

3X = 24

X = 24 = 8
3

La razón de a es
= =

Proporción:

Es la igualdad de
dos razones.

Igualdad de Ángulos:

Entre dos figuras semejantes, los ángulos
correspondientes son iguales.

Si A, B, C son puntos de f y A´, B´,
C´, los correspondientes puntos de f, entonces se cumple
que:

Relación entre
Volúmenes:

El cociente entre los volúmenes de dos figuras
semejantes es igual al cubo de la razón de la
semejanza.

Dos polígonos son semejantes si sus lados
son proporcionales y sus ángulos respectivamente
iguales.

Para saber que dos triángulos son semejantes basta
comprobar que se cumple alguna de las condiciones siguiente
llamadas criterios o casos de semejanza de
triángulos.

Criterio 1: Tienen dos pares de ángulos
respectivamente iguales.

Criterio 2: Tienen un ángulo igual y
proporcionales los lados que lo forman.

Criterio 3: Tienen tres lados proporcionales.

TEOREMA DE PITÀGORAS

"En cualquier triangulo rectángulo
el cuadrado de la hipotenusa es igual a la suma de los cuadrados
de lo catetos".

Ilustración:

a c C2= a2 +
b2

Dem: Trafiquemos el triangulo rectángulo tomado
de la

De la hipotenusa como base y luego tracemos su
altura.

Designemos Por x la distancia de un vértice al
punto en que la altura se toca con la hipotenusa. La distancia de
dicho punto al otro vértice es por tanto c-x.

La altura así trazada determina
rectángulos semejantes.

CUADRILÀTEROS

Polígono de cuatro lados. La suma de sus
ángulos interiores es 360. Los cuadriláteros tienen
dos diagonales.

Se clasifican en paralelogramos si tienen los dos pares
de lados opuestos iguales entre si.

Los paralelogramos son: los cuadrados (cuatro
lados iguales y los cuatro ángulos rectos),
rectángulos (los cuatro ángulos rectos)
rombos (cuatro lados iguales) romboides (no tienen
los lados iguales ni los cuatro ángulos
rectos).

CLASIFICACION:

PARALELOGRAMO:

Cuadrilátero cuyos dos pares de lados son iguales
entre si.

Para ver el
gráfico seleccione la opción "Descargar" del
menú superior

TRAPECIO:

Cuadrilátero con solamente dos lados opuestos
paralelos y dos no paralelos.

Para ver el
gráfico seleccione la opción "Descargar" del
menú superior

TRAPEZOIDE:

Cuadrilátero que no es paralelogramo ni trapecio, no
tiene ningún par de lados paralelos.

PARALELOGRAMOS

CLASIFICACION:

RECTANGULO:

Es el paralelogramo que tiene sus cuatro ángulos
iguales; pero en cuanto a sus lados son iguales solamente los
opuestos.

Para ver el
gráfico seleccione la opción "Descargar" del
menú superior

CUADRADOS:

Paralelogramo que tiene iguales sus cuatro ángulos y
sus cuatro lados.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

ROMBOS:

Paralelogramos con sus cuatro lados iguales e iguales
solamente los ángulos opuestos.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

ROMBOIDE:

Paralelogramo en que solamente son iguales entre si los
lados opuestos así como también los ángulos
opuestos.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

PROPIEDADES:

"La diagonal de un paralelogramo divide a
este en dos triángulos iguales".

Los pares de los lados opuestos son
iguales,
Los pares de ángulos opuestos son
iguales,
Cada dos ángulos contiguos son
suplementarios,
Sus diagonales se cortan en sus puntos medios.

CARACTERÍSTICAS:

Cuadrados: sus cuatro lados son iguales y sus
cuatro ángulos son rectos.

Rectángulos: sus cuatro ángulos son
rectos.

Rombos: sus cuatro lados son iguales.

Romboides: sus cuatro lados no son iguales y no
tienen ningún ángulo recto.

CONCEPTOS
BÀSICOS

Dos o más puntos son colineales si existe una
sola recta que los contenga.
Puntos Colineales:
Son rectas que están en un mismo plano pero no
se tocan, aunque se prolonguen indefinidamente.
Rectas Paralelas:
Cuando al caer una sobre otra (recta) no se inclina mas
de un lado ni de otro.
Rectas Perpendiculares:
Es la superficie plana limitada por líneas
rectas.
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
Polígono:
Es la figura que consta de tres lados, tres
ángulos y tres vértices.
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
Triángulo:
Es un polígono que consta de cuatro
lados.
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
Cuadrilátero:
Cuadrilátero cuyos dos pares de lados son
iguales entre si.
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
Paralelogramo:
Figura que tiene sus tres lados iguales.
Triángulo Equilátero:
Figura que tiene solamente dos lados iguales.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Triángulo Isósceles:
Figura que tiene sus tres lados desiguales.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Triángulo Escaleno:
Figura que tiene sus tres ángulos
agudos.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Triángulo Acutángulo:
Figura que tiene un ángulo recto, mide 90
grados.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Triángulo Rectángulo:
Figura que tiene un ángulo obtuso.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Triángulo Obtusángulo:
Figuras que tienen iguales sus tres ángulos y
sus lados son proporcionales.
Triángulos Semejantes:
Vértice:

Es la unión de dos rectas.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

16. Apotema:

Es la perpendicular que une el centro del
polígono con cualquiera de sus lados.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Es la recta que parte del vértice y es
perpendicular al lado opuesto.
Altura:
Es la semirrecta que divide al ángulo en dos
partes.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Bisectriz:
Es la recta perpendicular al segmento en su punto
medio.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Mediatriz:
Segmento que une el vértice con el punto medio
del lado opuesto.
Mediana:
Es el punto donde se cortan las tres medianas.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Baricentro:
Es el punto donde se unen las tres alturas.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Ortocentro:
Es el punto donde se unen las tres bisectrices.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Incentro:
Es el punto donde se unen las tres mediatrices.
Circucentro:
Cuando sus lados son semirrectas opuestas.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Ángulos opuestos por el
vértice:
Son dos ángulos situados al mismo lado de la
secante y también al mismo lado en cada una de las
rectas.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Ángulos Correspondientes:
Son ángulos colocados a uno y otro lado de la
recta secante.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Ángulos Alternos Internos:
Son dos ángulos externos, colocados a uno y otro
lado de la recta secante.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Ángulos Alternos Externos:
Es la recta que va desde el centro hasta la
circunferencia.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Radio:
Cualquier recta que pasa por el centro y cuyos extremos
están en la circunferencia.
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
Diámetro:
Recta cuyos extremos son dos puntos de la
circunferencia.
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
Cuerda:
Es la recta perpendicular al radio que une el centro
con el punto de la tangencia.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Tangente a una Circunferencia:
Cuando hay dos puntos comunes.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Secante a una Circunferencia:
Porción de recta comprendida entre el punto
medio de un arco de círculos y el de su
cuerda.
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
Flecha:
Son circunferencias que tienen el mismo centro.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Circunferencias Concéntricas:
Si tienen dos puntos comunes.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Circunferencias Secantes:
Si no tienen puntos comunes y la distancia entre sus
centros es mayor que la suma de sus radios.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Circunferencias Exteriores:
Si no tienen puntos comunes y la distancia entre sus
centros es menor que la suma de sus radios.
Circunferencias Interiores:
Si tienen un punto común y la distancia entre
sus centros es igual a la diferencia de sus radios.
Circunferencias Tangentes Interiores:
Si tienen un punto común y la distancia entre
sus centros es igual a la suma de sus radios.
Para ver el gráfico
seleccione la opción "Descargar" del menú
superior
Circunferencias Tangentes Exteriores:
Es la medida de la longitud de su contorno.
4 cms
1 cm.
Perímetro= 3 cms + 3 cms + 1 cm. + 1 cm. =
8 cms.
Perímetro de una figura plana:
Es la medida de su superficie.
3 cms
Area = 3 cms x 3cms = 9 cms2.
3 cms
Área de una figura plana:
Fórmulas de perímetros y
áreas de las principales figuras planas: