Hidroestática, hidrodinámica, termodinámica (página 2)

UNIDAD IV

Termodinámica

1. Temperatura

La temperatura es
la sensación física que nos
produce un cuerpo cuando entramos en contacto con
él.

Observamos cambios en los cuerpos cuando cambian su
temperatura,
por ejemplo, la dilatación que experimenta un cuerpo
cuando incrementa su temperatura. Esta propiedad se
usa para medir la temperatura de un sistema. Pensemos
en los termómetros que consisten en un pequeño
depósito de mercurio que asciende por un capilar a medida
que se incrementa la temperatura.

De una manera cualitativa, nosotros podemos describir la
temperatura de un objeto como aquella determinada por la
sensación de tibio o frío al estar en contacto con
él.

Esto es fácil de demostrar cuando dos objetos se
colocan juntos (los físicos lo definen como contacto
térmico), el objeto caliente se enfría mientras que
el más frío se calienta hasta un punto en el cual
no ocurren más cambios, y para nuestros sentidos, ambos
tienen el mismo grado de calor. Cuando
el cambio
térmico ha parado, se dice que los dos objetos (los
físicos los definen más rigurosamente como sistemas)
están en equilibrio térmico. Entonces
podemos definir la temperatura de un sistema diciendo
que la temperatura es aquella cantidad que es igual para ambos
sistemas cuando
ellos están en equilibrio
térmico.

Si nuestro experimento fuese hecho con más de dos
sistemas, encontraríamos que muchos sistemas pueden ser
llevados a equilibrio
térmico simultáneamente; el equilibrio
térmico no depende del tipo de objeto usado. Pero siendo
más preciso:

Si dos sistemas están separadamente en
equilibrio térmico con un tercero, entonces ellos deben
estar en equilibrio térmico entre
sí.

y ellos tienen la misma temperatura sin tomar en cuenta
el tipo de sistema que sean.

Lo expresado en letras itálicas es llamado
Ley Cero de la Termodinámica y puede ser
escrita más formalmente como:

"Si tres o más sistemas están en
contacto térmico entre si y todos en equilibrio al mismo
tiempo,
entonces cualquier par que se tome separadamente están
en equilibrio entre sí".

Ahora uno de los tres sistemas puede ser calibrado como
un instrumento para medir temperatura, definiendo así un
termómetro. Cuando uno calibra un termómetro, este se pone en contacto con el
sistema hasta que alcanza el equilibrio térmico,
obteniendo así una medida cuantitativa de la temperatura
del sistema. Por ejemplo, un termómetro clínico de
mercurio es colocado bajo la lengua del
paciente y se espera que alcance el equilibrio térmico con
su boca. Podemos ver como el líquido plateado (mercurio)
se expande dentro del tubo de vidrio y se puede
leer en la escala del
termómetro para saber la temperatura del
paciente.

¿Qué es un Termómetro?. Es un
instrumento que mide la temperatura de un sistema en forma
cuantitativa. Una forma fácil de hacerlo es encontrando
una sustancia que tenga una propiedad que
cambie de manera regular con la temperatura. La manera más
"regular" es de forma lineal "t(x)=ax+b ", donde t es la
temperatura y cambia con la propiedad x de la sustancia. Las
constantes a y b dependen de la sustancia usada y deben ser
evaluadas en dos puntos de temperatura específicos sobre
la escala, por
ejemplo, 32° para el punto congelamiento del agua y
212° para el punto de ebullición. Después se
aclara que este es el rango de una escala ya conocida como la
Fahrenheit.

Por ejemplo, el mercurio es líquido dentro del
rango de temperaturas de -38,9° C a 356,7° C ( la escala
Celsius se discute más adelante). Como un líquido,
el mercurio se expande cuando se calienta, esta expansión
es lineal y puede ser calibrada con exactitud.

1.1. El Desarrollo de
Termómetros y Escalas de Temperaturas.

Uno de los primeros intentos para hacer un
estándar de temperaturas ocurrió alrededor de AD
170, cuando Galeno ,en sus notas médicas, propone un
estándar de temperatura "neutral" completando cantidades
iguales para la ebullición del agua y el
hielo. Sobre cualquier lado de esta temperatura tenía
cuatro grados de calor y cuatro
grados de frío respectivamente.

Los primeros equipos usados para medir la temperatura
fueron llamado Termoscopios.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Figura 12. Termoscopios

Consistían en un bulbo de vidrio que tiene
un largo tubo extendido hacia abajo colocado dentro de un
recipiente que contiene agua con colorante (aunque Galileo en
1610 utilizó vino). Algo del aire contenido
dentro del bulbo se expulsa, por lo cual el líquido se
eleva a través del tubo para tomar su lugar. Como el
aire remanente
del bulbo se calienta o enfría, el nivel de líquido
en el tubo varia reflejo del cambio de la
temperatura del aire. Colocando una escala grabada sobre el tubo,
se puede medir en forma cuantitativa estas
fluctuaciones.

El aire dentro del bulbo es referido como medio
termométrico, siendo aquel medio cuya propiedad
cambia con la temperatura.

En 1641 el primer termómetro sellado que
usó líquido en vez de aire como medio
termométrico fue desarrollado por Ferdinand II, Gran Duque
de Toscana. Su termómetro usó un equipo sellado en
vidrio dentro del cual había alcohol, con
50 "grados" marcados sobre el tubo pero un "punto fijo" para el
cero de la escala no fue utilizado, Estos fueron referidos como
termómetros de "espíritu".

Robert Hook, párroco de la Sociedad Real, en
1664 usó un tinte rojo en alcohol. Su
escala, para la cual todos los grado representaban un igual
incremento de volumen
equivalente alrededor de 1/500 partes de el volumen del
líquido del termómetro, necesitó solo un
punto fijo. El seleccionó el punto de congelamiento del
agua. Por una escala presentada de esta manera, Hook
presentó que un mismo estándar puede ser
establecido para termómetros de tamaños diferentes.
El termómetro original de Hook quedó conocido como
un estándar del Gresham College y fue usado por la
Sociedad Real
hasta 1709. (El primer registro
meteorológico inteligible usó esta
escala).

En 1702, el astrónomo Ole Roemer de Copenhagen
basó su escala en dos puntos fijos: nieve (o hielo
comprimido) y el punto de ebullición del agua, y
registró la temperatura diaria en Copenhagen desde 1708 a
1709 con su termómetro.

Fue en 1724 que Gabriel Fahrenheit usó mercurio
como liquido termométrico. La expansión
térmica del mercurio es amplia y suavemente uniforme, esto
permite que no se adhiera a el vidrio y permanece líquido
ante un amplio rango de temperaturas. Su apariencia plateada hace
que sea fácil de leer. Fahrenheit describió como
calibró la escala de mercurio de su termómetro de
la siguiente manera:

" Colocando el termómetro en un mezcla
de sal de amonio o agua salada, hielo, y agua, un punto sobre
la escala pudo ser encontrado el cual llamé cero. Un
segundo punto fue obtenido de la misma manera, si la mezcla es
usada sin sal. Denotando este punto como 30. Un tercer punto
designado como 96 fue obtenido colocando el termómetro
en la boca para adquirir el calor del cuerpo
humano."

Sobre esta escala, Fahrenheit midió el punto de
ebullición del agua obteniendo 21 2. Después
adjudicó el punto de congelamiento del agua a 32
así que el intervalo entre el punto de congelamiento y
ebullición del agua puede ser representado por el
número racional 180. Temperaturas medidas sobre esta
escala son designadas como grados Fahrenheit
(°F).

En 1745 Carlos Linneo de Upsala, Suecia,
describió una escala en la cual el punto de congelamiento
del agua era 100 y el punto de ebullición cero haciendo
esto una escala centígrada. Anders Celsius (1701-1744)
usó la escala al revés en la cual cero
representó el punto de congelamiento y 100 el punto de
ebullición del agua, manteniendo los 100 grados entre los
dos puntos. En 1948 el término Grado Centígrado fue
reemplazado por el de Grados Celsius. Temperaturas medidas sobre
una escala centígrada, con el punto de congelamiento del
agua como cero, son designadas como grados Celsius
(°C).

Para convertir de grado Centígrado a Fahrenheit
multiplique por 1,8 y sume 3 2.

°F=1,8° C+32. ecc.26

En 1780, J.A. C. Charles, físico francés,
presentó que para un mismo incremento de temperatura,
todos los gases tienen
el mismo aumento de volumen. Porque los coeficientes de
expansión de los gases son tal
que están muy cerca uno del otro, con esto es posible
establecer una escala de temperatura basada en un solo punto fijo
en vez de dos, tal como en la Fahrenheit o Celsius. Esto nos
lleva a termómetro que usen gas como medio
termométrico.

Para ver el gráfico seleccione la
opción "Descargar" del menú superior

Figura 13. Termómetro de
gas

En este termómetro de gas a volumen
constante el bulbo B que contiene hidrógeno (por ejemplo)
bajo un cierta presión
,se conecta con un manómetro de mercurio por medio de un
tubo de volumen muy pequeño. (El bulbo B es la
porción sensible a la temperatura y debe procurarse que
todo sea de mercurio). El nivel de mercurio en C puede
adjudicarse al elevarse o no el nivel en el reservorio R. La
presión
del hidrógeno la cual es "x" varía en
relación lineal con la temperatura, es la diferencia entre
los niveles D y C más la presión encima de
D.

P. Chappuis in 1887 dirigió extensos estudios
sobre los termómetros de gas con presión constante
o con volumen constante usando hidrógeno, nitrógeno
y bióxido de carbono como
medios
termométricos. Basado en estos resultados, el Comite
Internacional de Pesos y Medidas adoptó la escala de
hidrógeno a volumen constante tomando como puntos fijos el
punto de hielo (0° C) y de vapor (100° C) como escala
práctica para la meteorología
internacional.

Experimentos con termómetros de gas han divulgado
que es muy pequeña la diferencia en la lectura de
temperaturas utilizando diferentes gases. Así es posible,
fijar una escala de temperatura que sea independiente del medio
termométrico si este es un gas a baja presión. En
este caso, todos los gases se comportan como un gas ideal y
tienen una relación muy simple entre la presión,
temperatura y volumen: "pV=(constante)T. "

Esta temperatura es llamada temperatura
termodinámica y es aceptada en la actualidad como
medida fundamental de temperatura. Note que hay una
definición natural del cero en esta escala; es el punto
donde la presión del gas ideal se hace cero, por lo tanto
la temperatura es cero. La discusión sobre el cero
absoluto se hará posteriormente. En 1933, El Comité
Internacional de Pesos y Medidas adoptó como punto fijo el
punto triple del agua, (la temperatura a la cual el agua el
hielo, agua líquido y vapor coexisten en equilibrio), este
valor es
273,16, la unidad de temperatura de esta escala fue llamada
Kelvin, por Lord Kelvin (Williams Thompson) 1824-1907, y su
símbolo es K. (no utiliza grados).

Para convertir de Celsius a Kelvin sumo
273,16:

K=°C+273,16 ecc.27

Temperatura Termodinámica es la temperatura
fundamental, su unidad es el Kelvin la cual se define como una
fracción de 1/273,16 de la temperatura termodinámica del punto triple del
agua.

Sir William Siemens en 1871 propuso un termómetro
donde medio termométrico es un conductor metálico
cuya resistencia
cambia con la temperatura. El platino no se oxida a altas
temperaturas y tiene un cambio relativamente uniforme con la
temperatura en un amplio rango. El termómetro de
resistencia de
platino es ampliamente usado como termómetro
termoeléctrico y cubre un rango de temperaturas que va
desde -260° C a 1235° C.

Algunas temperatura fueron adoptadas como Referencias
Primarias tal como las definió la Escala Internacional de
Temperaturas Prácticas en 1968. La Escala de Internacional
de Temperaturas en 1990 adoptó por el Comité
Internacional de Pesos y Medidas los siguientes estándares
mantenidos desde 1989. Entre 0,65K y 5,0 K, la temperatura se
definió en términos de la presión de vapor
(relación de temperaturas del isótopo de Helio).
Entre 3,0 K y el punto triple del Neón (24,5561 K) la
temperatura se definió por medio de un termómetro
de gas (Helio). Entre el punto triple del hidrógeno
(13,8033 K) y el punto de congelamiento de la plata (961,78 oC)
la temperatura se definió por medio de termómetros
de resistencia de platino. Por encima del punto de congelamiento
de la plata la temperatura se definió en términos
de la Ley de Radiación
de Planck.

T.J. Seebeck en 1826 descubrió que cuando
alambres de diferentes metales son
fusionados en un terminal y calentados, fluye corriente de uno a
otro. La fuerza
electromotriz generada puede ser cuantitativamente relacionada
con la temperatura y así el sistema puede ser usado como
termómetro, conocido como termocouple. La termocouple es
usada en la industria y
diferentes metales son
usados: níquel / aluminio y
platino / platino-rodio, por ejemplo. El Instituto Nacional de
Estándares y Tecnologías (NIST) mantiene bases de datos
para estandarizar termómetros.

Para las medidas a muy bajas temperaturas, la
susceptibilidad magnética de una sustancia
paramagnética es usada como una cantidad física
termométrica. Para algunas sustancias, la susceptibilidad
magnética varía inversamente con la temperatura.
Cristales como (cerrous magnesium nitrate y chromic potassum
alum) han sido usados para medir temperaturas por debajo de 0,05
K; estos cristales son calibrados en un rango de helio
líquido. Este diagrama y las
últimas ilustraciones de este texto fueron
tomadas del archivo de
imágenes del Laboratorio de
Bajas Temperaturas de la Universidad
Tecnológica de Helsinki. Para estas temperaturas tanto o
más bajas que estas, el termómetro es
también usado como mecanismo de enfriamiento. Algunos
laboratorios de bajas temperaturas conducen interesantes
aplicaciones e investigaciones
teóricas sobre como alcanzar la temperatura más
baja posible, como trabajarlas y encontrarle
aplicaciones.

2. Ley de los gases
ideales (ecuación de estado)

Según la teoría
atómica las moléculas pueden tener o no cierta
libertad de
movimientos en el espacio; estos grados de libertad
microscópicos están asociados con el concepto de orden
macroscópico. Las libertad de movimiento de
las moléculas de un sólido está restringida
a pequeñas vibraciones; en cambio, las moléculas de
un gas se mueven aleatoriamente, y sólo están
limitadas por las paredes del recipiente que las
contiene.

Se han desarrollado leyes
empíricas que relacionan las variables
macroscópicas en base a las experiencias en laboratorio
realizadas. En los gases ideales, estas variables
incluyen la presión (p), el volumen (V) y la
temperatura (T). 

La ley de
Boyle – Mariotte relaciona inversamente las
proporciones de volumen y presión de un gas, manteniendo
la temperatura constante:

P1. V1 =
P2 .
V2<> 
ecc.28

La ley de Gay-Lussac afirma que el volumen de un
gas, a presión constante, es directamente proporcional a
la temperatura absoluta:

V1/T1=V2/T2<>
ecc.29

La ley de Charles sostiene que, a volumen
constante, la presión de un gas es directamente
proporcional a la temperatura absoluta del sistema:

P1/T1=P2/T2 ecc.30

En ambos casos la temperatura se mide en kelvin (273
ºK = 0ºC) ya que no podemos dividir por cero, no existe
resultado.

De las tres se deduce la ley universal de los
gases:

P1/T1=P2/T2
=V1/T1=V2/T2<> =
(P1V1)/T1 =
(P2V2)/T2<> ecc.31

3. Teoría
Cinética de los Gases

El comportamiento
de los gases, enunciadas mediante las leyes
anteriormente descriptas, pudo explicarse satisfactoriamente
admitiendo la existencia del átomo. 

El volumen de un gas: refleja simplemente la distribución de posiciones de las
moléculas que lo componen. Más exactamente, la
variable macroscópica V representa el espacio
disponible para el movimiento de
una molécula. 

La presión de un gas, que puede medirse
con manómetros situados en las paredes del recipiente,
registra el cambio medio de momento lineal que experimentan las
moléculas al chocar contra las paredes y rebotar en
ellas. 

La temperatura del gas es proporcional a la
energía cinética media de las moléculas, por
lo que depende del cuadrado de su velocidad. 

Figura 14. Comportamiento
de los gases

La reducción de las variables
macroscópicas a variables mecánicas como la
posición, velocidad,
momento lineal o energía cinética de las
moléculas, que pueden relacionarse a través de
las leyes de la
mecánica de Newton, debería de
proporcionar todas las leyes empíricas de los gases. En
general, esto resulta ser cierto.

La teoría física que relaciona las
propiedades de los gases con la mecánica clásica se denomina
teoría cinética de los gases. Además de
proporcionar una base para la ecuación de estado del gas
ideal. La teoría cinética también puede
emplearse para predecir muchas otras propiedades de los gases,
entre ellas la distribución estadística de las velocidades moleculares
y las propiedades de transporte
como la conductividad térmica, el coeficiente de
difusión o la viscosidad.

3.1. Densidad de un
gas

En un determinado volumen las moléculas de gas
ocupan cierto espacio. Si aumenta el volumen (imaginemos un globo
lleno de aire al que lo exponemos al calor aumentando su
temperatura), la cantidad de moléculas (al tener mayor
espacio) se distribuirán de manera que encontremos menor
cantidad en el mismo volumen anterior. Podemos medir la cantidad
de materia, ese
número de moléculas, mediante una magnitud
denominada masa. La cantidad de moléculas, la masa, no
varía al aumentar o disminuir (como en este caso) el
volumen, lo que cambia es la relación masa – volumen. Esa
relación se denomina densidad
(ρ). La densidad es
inversamente proporcional al volumen (al aumentar al doble el
volumen , manteniendo constante la masa, la densidad disminuye a
la mitad) pero directamente proporcional a la masa (si aumentamos
al doble la masa, en un mismo volumen, aumenta al doble la
densidad).

ρ = m/V ecc.32

3.2. Hipótesis de Avogadro

Esta hipótesis
establece que dos gases que posean el mismo volumen (a igual
presión y temperatura) deben contener la misma cantidad de
moléculas. 

Cada molécula, dependiendo de los átomos
que la compongan, deberán tener la misma masa. Es
así que puede hallarse la masa relativa de un gas de
acuerdo al volumen que ocupe. La hipótesis de Avogadro permitió
determinar la masa molecular relativa de esos
gases. 

Analicemos el orden lógico que
siguió:

1. La masa de 1 litro de cualquier gas es la masa de
   todas las moléculas de ese gas.
3. Un litro de cualquier gas contiene el mismo
   número de moléculas de cualquier otro
   gas
4. Por lo tanto, un litro de un gas posee el doble de
   masa de un litro otro gas si cada molécula del primer
   gas pesa el doble de la molécula del segundo
   gas.
5. En general las masas relativas de las
   moléculas de todos los gases pueden determinarse pesando
   volúmenes equivalentes de los gases.

En condiciones normales de presión y temperatura
(CNPT) [ P = 1 atm y T = 273 ºK ] un
litro de hidrógeno pesa 0,09 g  y un litro de
oxígeno
pesa 1,43 g. Según la hipótesis de
Avogadro ambos gases poseen la misma cantidad de
moléculas. La proporción de los pesos entre ambos
gases es: 1,43 : 0,09 = 15,9 (aproximadamente) 16. Es la
relación que existe entre una molécula de oxígeno
e hidrógeno es 16 a 1. Las masas atómicas relativas
que aparecen en la tabla
periódica están consideradas a partir de un
volumen de 22,4 litros en CNPT.

3.3. Ley de los Gases Generalizada

Como consecuencia de la hipótesis de Avogadro
puede considerarse una generalización de la ley de los
gases. Si el volumen molar (volumen que ocupa un mol de
molécula de gas) es el mismo para todos los gases en CNPT,
entonces podemos considerar que el mismo para todos los gases
ideales a cualquier temperatura y presión que se someta al
sistema. Esto es cierto por que las leyes que gobiernan los
cambios de volumen de los gases con variaciones de temperatura y
presión son las mismas para todos los gases
ideales.

Se denomina ecuación de estado a la
relación que existe entre las variables p,
V, y T. La ecuación de estado más
sencilla es la de un gas ideal

pV=nRT ecc. 33

, donde n representa el número de moles,
R la constante de los gases R=0,082 atm·l/(K mol)
ó (8,31 J/mol*K) y T (grados kelvin).

4. Calorimetría y
Termodinámica

La Termodinámica campo de la física que
describe y relaciona las propiedades físicas de sistemas
macroscópicos (conjunto de materia que se
puede aislar espacialmente y que coexiste con un entorno infinito
e imperturbable) de materia y energía. El estado de
un sistema macroscópico en equilibrio puede describirse
mediante variables termodinámicas, propiedades medibles
como la temperatura, la presión o el volumen. Es posible
identificar y relacionar entre sí muchas otras variables
(como la densidad, el calor específico, la compresibilidad
o el coeficiente de expansión térmica), con lo que
se obtiene una descripción más completa de un
sistema y de su relación con el entorno. Cuando un sistema
macroscópico pasa de un estado de equilibrio a otro, se
dice que tiene lugar un proceso
termodinámico.

Calor una forma de energía: Cuando dos
sistemas, a temperaturas diferentes, se ponen en contacto, la
temperatura final que ambos alcanzan tiene un valor
intermedio entre las dos temperaturas iniciales. Ha habido una
diferencia de temperatura en estos sistemas. Uno de ellos ha
perdido "calor" (su variación de temperatura es menor que
cero ya que la temperatura final es menor que la inicial) y el
otro ha ganado "calor" (su variación de temperatura es
positiva). La cantidad de calor (cedida uno al otro) puede
medirse, es una magnitud escalar que suele ser representada
mediante la letra Q. Las unidades para medir el calor son la
caloría, kilo caloría (1000 cal), etc.

La caloría puede definirse como la "cantidad de
calor" necesaria para elevar en un grado de temperatura, un gramo
(masa) de materia: 1 cal / 1ºC.1 g

Durante mucho tiempo se
pensó que el calor era una especie de "fluido" que pasaba
de un cuerpo a otro. Hoy se sabe que el calor es una onda
electromagnética (posee la misma naturaleza que la
luz) y su
emisión depende de la vibración de los electrones
de los átomos que forman el sistema (véase mecánica cuántica).

4.1. Capacidad calórica y Calor
específico

Las sustancias difieren entre sí en la cantidad
de calor que se necesita para producir, en una unidad de masa
dada, un determinado aumento de temperatura. La relación
directamente proporcional entre la variación
de la cantidad de calor (ΔQ) y la variaciσn de
temperatura (ΔT) se denomina capacidad
calórica.

C = ΔQ / ΔT

Atención: la palabra capacidad puede
sugerir, erróneamente, que creamos que nos referimos a "la
cantidad de calor que un cuerpo puede contener", mientras que lo
que realmente significa es el calor añadido por unidad
de aumento de temperatura.

Decimos que una cantidad de calor
D Q se
transfiere desde el sistema de mayor temperatura al sistema de
menor temperatura.

La cantidad de calor transferida es proporcional al
cambio de temperatura D T.

La constante de proporcionalidad C se denomina
capacidad calorífica del sistema.

D
Q=C·D T ecc.34

Si los cuerpos A y B son los dos componentes de un
sistema aislado, el cuerpo que está a mayor temperatura
transfiere calor al cuerpo que está a menos temperatura
hasta que ambas se igualan. Si
TA>TB

El cuerpo A cede calor: D
QA=CA·(T-TA),
entonces D
QA<0

El cuerpo B recibe calor: D
QB=CB·(T-TB),
entonces D
QB<0

Como D
QA+D QB=0. La
temperatura de equilibrio, se obtiene mediante la media
ponderada

T =
(CATA+CBTB)/(CA+CB)
ecc. 35

La capacidad calorífica de la unidad de masa se
denomina calor específico c.

C = mc

La fórmula para la transferencia de calor entre
los cuerpos se expresa en términos de la masa m
del calor específico c y del cambio de
temperatura.

D
Q=m·c·(Tf-Ti) ecc.36

donde Tf es la temperatura final y
Ti es la temperatura inicial.

El calor específico es la cantidad de calor que
hay que suministrar a un gramo de una sustancia para que eleve en
un grado centígrado su temperatura. Joule demostró
la equivalencia entre calor y trabajo 1cal=4.186 J. Por razones
históricas la unidad de calor no es la misma que la de
trabajo, el calor se suele expresar en
calorías.

El calor específico del agua es c=1 cal/(g
ºC). Hay que suministrar una caloría para que un
gramo de agua eleve su temperatura en un grado
centígrado.

 Fundamentos físicos

Cuando varios cuerpos a diferentes temperaturas se
encuentran en un recinto adiabático se producen
intercambios caloríficos entre ellos alcanzándose
la temperatura de equilibrio al cabo de cierto tiempo. Cuando se
ha alcanzado este equilibrio se debe cumplir que la suma de las
cantidades de calor intercambiadas es cero.

Se define calor específico "c" como la
cantidad de calor que hay que proporcionar a un gramo de
sustancia para que eleve su temperatura en un grado
centígrado. En el caso particular del agua c vale 1
cal/(g ºC) ó 4186 J(kg ºK).

La unidad de calor específico que más se
usa es cal/(g ºC) sin embargo, debemos de ir
acostumbrándonos a usar el Sistema Internacional de
Unidades de Medida, y expresar el calor específico en
J/(kg ºK). El factor de conversión es
4186.

CUADRO 3. Calor específico de
algunos elementos

La cantidad de calor recibido o cedido por un cuerpo se
calcula mediante la siguiente fórmula

Q=m·c·(Tf-Ti) ecc.37

Donde m es la masa, c es el calor
específico, Ti es la temperatura inicial
y Tf la temperatura final

• Si Ti>Tf el cuerpo
  cede calor Q<0
• Si Ti<Tf el cuerpo
  recibe calor Q>0

4.2. Cambios de estado

Normalmente, una sustancia experimenta un cambio de
temperatura cuando absorbe o cede calor al ambiente que
le rodea. Sin embargo, cuando una sustancia cambia de fase
absorbe o cede calor sin que se produzca un cambio de su
temperatura. El calor Q que es necesario aportar para que
una masa m de cierta sustancia cambie de fase es igual
a

Q=mL ecc. 38

donde L se denomina calor latente de la sustancia
y depende del tipo de cambio
de fase.

Por ejemplo, para que el agua cambie
de sólido (hielo) a líquido, a 0ºC se
necesitan 334×103 J/kg. Para que cambie de
líquido a vapor a 100 ºC se precisan
2260·103 J/kg.

En la siguiente tabla, se proporcionan los datos referentes
a los cambios de estado de algunas sustancias.

CUADRO 4. Datos referentes
a los cambios de estado de algunas sustancias

Los cambios de estado se pueden explicar de forma
cualitativa del siguiente modo:

En un sólido los átomos y moléculas
ocupan las posiciones fijas de los nudos de una red cristalina. Un
sólido tiene en ausencia de fuerzas externas un volumen
fijo y una forma determinada.

Los átomos y moléculas vibran, alrededor
de sus posiciones de equilibrio estable, cada vez con mayor
amplitud a medida que se incrementa la temperatura. Llega un
momento en el que vencen a las fuerzas de atracción que
mantienen a los átomos en sus posiciones fijas y el
sólido se convierte en líquido. Los átomos y
moléculas siguen unidos por las fuerzas de
atracción, pero pueden moverse unos respecto de los otros,
lo que hace que los líquidos se adapten al recipiente que
los contiene pero mantengan un volumen constante.

Cuando se incrementa aún más la
temperatura, se vencen las fuerzas de atracción que
mantienen unidos a los átomos y moléculas en el
líquido. Las moléculas están alejadas unas
de las otras, se pueden mover por todo el recipiente que las
contiene y solamente interaccionan cuando están muy
próximas entre sí, en el momento en el que chocan.
Un gas adopta la forma del recipiente que lo contiene y tiende a
ocupar todo el volumen disponible.

Un ejemplo clásico en el que se usan los
conceptos de calor específico y calor latente es el
siguiente:

Determinar el calor que hay que suministrar para
convertir 1g de hielo a -20 ºC en vapor a 100ºC. Los
datos son los siguientes:

2. Calor específico del hielo
   ch=2090 J/(kg K)
3. Calor de fusión
   del hielo  Lf=334·103
   J/kg
4. Calor específico del agua c=4180 J/(kg
   K)
5. Calor de vaporización del agua
   Lv=2260·103
   J/kg

Etapas:

2. Se eleva la temperatura de 1g de hielo de -20ºC
   a 0ºC

Q1=0,001 x 2090 x(0-(-20))=41,8
J

3. Se funde el hielo

Q2=0,001 x 334×103 =334
J

4. Se eleva la temperatura del agua de 0º C a 100
   ºC

Q3=0,001x4180x(100-0)=418
J

5. Se convierte 1 g de agua a 100ºC en vapor a la
   misma temperatura

Q4=0,001 x 2260×103=2260
J

El calor total
Q=Q1+Q2+Q3+Q4=3053,8
J.

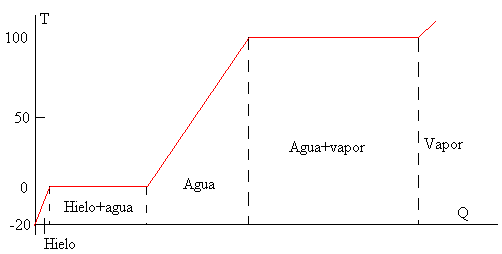
Figura 15. Diagrama de
proceso de
cambio de fase Hielo – Vapor

 En la figura 15, se muestra
cómo se va incrementando la temperatura a medida que se
aporta calor al sistema. La vaporización del agua requiere
de gran cantidad de calor como podemos observar en la
gráfica (no está hecha a escala) y en los
cálculos realizados en el ejemplo.

Si disponemos de una fuente de calor que suministra una
energía a razón constante de q J/s podemos
calcular la duración de cada una de las
etapas 

Los sistemas físicos que encontramos en la
Naturaleza
consisten en un agregado de un número muy grande de
átomos.

La materia está en uno de los tres estados:
sólido, líquido o gas: En los sólidos, las
posiciones relativas (distancia y orientación) de los
átomos o moléculas son fijas. En los
líquidos las distancias entre las moléculas son
fijas, pero su orientación relativa cambia continuamente.
En los gases, las distancias entre moléculas, son en
general, mucho más grandes que las dimensiones de las
mismas. Las fuerzas entre las moléculas son muy
débiles y se manifiestan principalmente en el momento en
el que chocan. Por esta razón, los gases son más
fáciles de describir que los sólidos y que los
líquidos.

El gas contenido en un recipiente, está formado
por un número muy grande de moléculas,
6,02×1023 moléculas en un mol de sustancia.
Cuando se intenta describir un sistema con un número tan
grande de partículas resulta inútil (e imposible)
describir el movimiento individual de cada componente. Por lo que
mediremos magnitudes que se refieren al conjunto: volumen ocupado
por una masa de gas, presión que ejerce el gas sobre las
paredes del recipiente y su temperatura. Estas cantidades
físicas se denominan macroscópicas, en el sentido
de que no se refieren al movimiento individual de cada
partícula, sino del sistema en su conjunto.

4.3. Transferencia de calor

Transferencia de energía causada por la
diferencia de temperatura entre dos partes adyacentes de un
cuerpo. El calor se transfiere mediante convección,
radiación
o conducción. Aunque estos tres procesos
pueden tener lugar simultáneamente, puede ocurrir que uno
de los mecanismos predomine sobre los otros dos.

Conducción: es la única forma de
transferencia de calor en los sólidos.

Si consideramos una lámina cuya área de
sección recta sea A y espesor
(Δx), expuesta a diferentes
temperaturas (ΔT) en cada una de sus caras, se puede medir
la cantidad de calor (ΔQ) que fluye perpendicularmente a
las caras en un determinado tiempo (Δt). La relaciσn
(directamente proporcional) entre cantidad de calor (ΔQ) y
el tiempo (Δt) determina la velocidad de
transmisión (v) del calor a
través del área A; mientras que la relación
(directamente proporcional) entre la variación de
temperatura (ΔT) y el espesor
(Δx) se llama gradiente
de temperatura. La igualdad se
obtiene mediante una constante de proporcionalidad (k) llamada
conductividad térmica.

ΔQ/Δt = – KA
(ΔT/Δx)

La dirección de flujo del calor será
aquella en la que aumenta x; como el calor fluye en
dirección en que disminuye T, se introduce
un signo menos en la ecuación. Lo que significa que
ΔQ/Δt es positiva cuando
ΔT/Δx es
negativa.

También puede aplicarse esta ecuación a
una varilla metálica de longitud L y sección
transversal constante A en la cual se ha alcanzado un estado
estacionario (la temperatura en cada uno de los extremos es
constante en el tiempo), por consiguiente, la temperatura decrece
linealmente a lo largo de la varilla.

ΔQ/Δt = – KA
(ΔT/L)

Los materiales
como el oro, la plata o el cobre tienen
conductividades térmicas elevadas y conducen bien el
calor, mientras que materiales
como el vidrio o el amianto tienen conductividades cientos e
incluso miles de veces menores; conducen muy mal el calor, y se
conocen como aislantes.

4.4. Convección

Si existe una diferencia de temperatura en el interior
de un fluido (líquido o un gas) es casi seguro que se
producirá un movimiento llamado
convección.

Si se calienta un líquido o un gas, su densidad
(masa por unidad de volumen) suele disminuir, el fluido
más caliente y menos denso asciende, mientras que el
fluido más frío y más denso desciende. Este
tipo de movimiento, debido exclusivamente a la no uniformidad de
la temperatura del fluido, se denomina convección natural.
La convección forzada se logra sometiendo el fluido a un
gradiente de presiones, con lo que se fuerza su
movimiento de acuerdo a las leyes de la mecánica de
fluidos.

Si calentamos una cacerola llena de agua, el
líquido más próximo al fondo se calienta por
el calor que se ha transmitido por conducción a
través de la cacerola. Al expandirse, su densidad
disminuye y como resultado de ello el agua caliente asciende y
parte del fluido más frío baja hacia el fondo, con
lo que se inicia un movimiento de circulación. El
líquido más frío vuelve a calentarse por
conducción, mientras que el líquido más
caliente situado arriba pierde parte de su calor por
radiación y lo cede al aire situado por encima.

4.5. Radiación

La radiación presenta una diferencia fundamental
respecto a la conducción y la convección: las
sustancias que intercambian calor no tienen que estar en
contacto, sino que pueden estar separadas por un vacío. La
vibración de los electrones (salto cuántico)
está determinada por la cantidad de energía
absorbida. Esta energía es liberada en forma de
radiación (luz, calor, rayos
x) dependiendo de la energía de estimulación
administrada.

4.6. Equivalente mecánico del
Calor

Si el calor es precisamente otra forma de
energía, cualquier unidad de energía puede ser una
unidad de calor. El tamaño relativo de las "unidades de
calor" y las "unidades mecánicas" puede encontrarse a
partir de los experimentos en
los cuales una cantidad conocida de energía
mecánica, medida en joules, se añade al sistema
(recipiente de agua, por ejemplo). Del aumento de temperatura
medido puede calcularse cuanto calor (en calorías)
tendremos que añadir a la muestra de agua
para producir el mismo efecto. De esa manera puede calcularse la
relación entre Joule y calorías, es decir, el
llamado equivalente mecánico del calor.

Originalmente Joule utilizó un aparato en el cual
unas pesas, al caer, hacían girar un conjunto de paletas
sumergidas en agua. La pérdida de energía
mecánica (debido al rozamiento) se calculaba conociendo
las pesas y las alturas de las cuales caían. La
energía calórica equivalente era determinada a
través de la masa de agua y su aumento de
temperatura.

Los resultados aportados fueron: 1 kcal = 1000 cal =
4186 joules.

Es decir 4186 Joules de energía elevarán
la temperatura de 1 Kg. de agua en 1 ºC, lo mismo que 1000
calorías.

4.7. Calor y Trabajo

Ni el calor ni el trabajo son
propiedades de un cuerpo en el sentido de poder
asignarle un valor a la cantidad "contenida" en el sistema.
El trabajo es
una medida de la energía trasferida por medios
mecánicos mientras que el calor, en cambio, es una medida
de la energía transferida por medio de una diferencia de
temperatura.

La Termodinámica estudia la transferencia de
energía que ocurre cuando un sistema sufre un determinado
proceso (termodinámico) que produce un cambio llevando de
un estado a otro del sistema

<>

Figura 16. Trabajo
mecánico

Si aplicamos una fuerza sobre una superficie obtendremos
una presión sobre ese lugar. La fuerza aplicada, al
provocar un desplazamiento, genera trabajo mecánico. En el
caso de la presión, que actúa sobre las paredes de
un cuerpo extensible, el ensanchamiento de este produce
variación de volumen, el que está asociado con el
trabajo mecánico también.

F = Pr.Sup

W = (Pr. Sup Δx )à ΔV = W =
PrΔV

W = F Δx

4.8. Ley Cero

Si dos sistemas distintos están en equilibrio
termodinámico con un tercero, también tienen que
estar en equilibrio entre sí.

Si uno de estos sistemas se pone en contacto con un
entorno infinito situado a una determinada temperatura, el
sistema acabará alcanzando el equilibrio
termodinámico con su entorno, es decir, llegará a
tener la misma temperatura que éste. (El llamado entorno
infinito es una abstracción matemática
denominada depósito térmico; en realidad basta con
que el entorno sea grande en relación con el sistema
estudiado).

4.9. Primera Ley

Analicemos una situación imaginaria para
redondear una idea: si tenemos un sistema que cambie de un estado
inicial de equilibrio i, a un estado final de equilibrio f, en un
forma determinada, tendremos a Q como el calor absorbido por el
sistema y W como el trabajo hecho por el sistema; después
calculamos el valor de Q – W. Ahora, cambiemos el sistema
manteniendo, por supuesto, el mismo estado i para llegar hasta
el estado
final f, pero en esta ocasión utilizamos un camino
diferente. Repetimos el procedimiento una
y otra vez usando diferentes caminos en cada caso. Nos
encontramos que en todos los intentos Q – W mantiene su
valor numérico siempre igual. La explicación se
debe a que: aunque la magnitud de Q y W, separadamente, dependen
del camino tomado, Q – W no depende de cómo pasamos
de un estado a otro, sino sólo de ambos estados, el
inicial y el final (de equilibrio).

Por lo visto en mecánica, que cuando un objeto se
mueve de un punto a otro en un campo gravitacional en ausencia de
fricción, el trabajo hecho depende solo de las posiciones
de los puntos y no de la trayectoria por la que el cuerpo se
mueve. Podemos concluir que hay una energía potencial, en
función
de las coordenadas espaciales del cuerpo, cuya diferencia entre
su valor final y su valor inicial es igual al trabajo hecho al
desplazar el cuerpo. En termodinámica se encuentra
experimentalmente que, cuando en un sistema ha cambiado su estado
i al f, la cantidad Q – W dependen solo de las coordenadas
iniciales y finales y no del camino tomado entre estos puntos
extremos. Se concluye que hay una función de
las coordenadas termodinámicas cuyo valor final menos su
valor inicial es igual al cambio Q – W en el proceso. A
esta función le llamamos función de la
energía interna (la que se representa mediante la letra
U)

La diferencia entre la energía interna del
sistema en el estado f (U f ) y el estado inicial i
(Ui) es solo el cambio de energía interna del
sistema, y esta cantidad tiene un valor determinado
independientemente de la forma en que el sistema pasa del estado
i al estado f: Tenemos entonces que

U f – U i. =
ΔU = Q – U
ecc.39

Como sucede con la energía potencial,
también para que la energía interna, lo que importa
es su cambio. Esta ecuación se conoce como la primera ley
de la termodinámica, al aplicarla debemos recordar que Q
se considera positiva cuando el calor entra al sistema y que W
será positivo cuando el trabajo lo hace el sistema. A la
función interna U, se puede ver como muy abstracta en este
momento. En realidad, la termodinámica clásica no
ofrece una explicación para ella, además es una
función de estado que cambia en una forma predecible. La
primera ley de la termodinámica, se convierte entonces en
un enunciado de la ley de la conservación de la
energía para los sistemas termodinámicos. La
energía total de un sistema de partículas (U),
cambia en una cantidad exactamente igual a la cantidad que se le
agrega al sistema, menos la cantidad que se le quita.

El hecho que consideremos que el valor de Q sea positivo
cuando el calor entra al sistema y que W sea positivo cuando la
energía sale del sistema como trabajo está
determinado por el estudio de las máquinas
térmicas, que provocó inicialmente el estudio
de la termodinámica. Simplemente es una buena forma
económica tratar de obtener el máximo trabajo con
una maquina de este tipo, y minimizar el calor que debe
proporcionársele a un costo importante.
Estas naturalmente se convierten en cantidades de interés.

Si nuestro sistema sólo sufre un cambio muy
pequeño, infinitesimal, en su estado, se absorbe nada
más una cantidad infinitesimal de calor y se hace solo una
cantidad infinitesimal de trabajo, de tal manera que el cambio de
energía interna también es infinitesimal. Aunque la
cantidad infinitesimal de trabajo y la cantidad infinitesimal de
calor no son diferencias exactas (el por que va más
allá de este apunte por lo que deberá acceder a un
texto de
termodinámica avanzado), podemos escribir la primera ley
diferencial en la forma: dU = dQ – dW.

Podemos definir la primera ley diciendo: todo sistema
termodinámico en un estado de equilibrio, tiene una
variable de estado llamada energía interna U cuyo cambio
dU en un proceso diferencial está dado por la
ecuación antes escrita.

La primera ley de la termodinámica se aplica a
todo proceso de la naturaleza que parte de un estado de
equilibrio y termina en otro. Un sistema esta en estado de
equilibrio cuando podemos describirlo por medio de un grupo
apropiado de parámetros constantes del sistema como
presión ,el volumen, temperatura, campo
magnético y otros. La primera ley sigue
verificándose si los estados por los que pasa el sistema
de un estado inicial (equilibrio), a su estado final
(equilibrio), no son ellos mismos estados de equilibrio. Por
ejemplo podemos aplicar la ley de la termodinámica a la
explosión de un cohete en un tambor de acero
cerrado.

La primera ley establece que la energía se
conserva, sin embargo, cuando un cuerpo caliente y otro
frío se ponen en contacto no ocurre que el primero se pone
más caliente y el segundo más frío. Si bien
no estamos violando la primera ley, esta no restringe nuestra
capacidad de convertir trabajo en calor o calor en trabajo,
especifica únicamente que la energía debe
conservarse durante el proceso. La realidad es que, aunque
podamos convertir una pequeña cantidad de trabajo en
calor, no se ha podido hallar un procedimiento que
convierta por completo una cantidad dada de calor en trabajo. La
segunda ley de la termodinámica se ocupa de este problema
y aunque su contenido pueda parecer esotérico o abstracto,
su aplicación ha demostrado ser extremadamente
práctico.

Procesos reversible e irreversibles: Consideremos
un sistema típico en equilibrio termodinámico: una
masa m de gas real encerrado en un dispositivo cilíndrico
(cuyas paredes laterales son aislantes térmicos mientras
que el piso es conductor) y un émbolo que mantiene un
volumen V, dentro del cual el gas se encuentra a una
presión p y una temperatura T, los que se mantienen
constantes con el tiempo. En la base del cilindro tenemos una
fuente de calor para mantener la temperatura.

Podemos variar de muchas maneras a otro estado de
equilibrio en el cual la temperatura T sea la misma pero su
volumen se reduzca a la mitad. Analicemos dos casos
extremos.

I. Hacemos bajar el
émbolo muy rápidamente y se espera que se
establezca el equilibrio. Durante el proceso el gas es turbulento
y su presión y temperatura no están bien definidas.
Los estados intermedios en el cual se desarrolla el proceso no
son de equilibrio. El proceso se denomina
irreversible.

II. Si hacemos bajar el
émbolo muy lentamente (despreciando a la fricción),
la temperatura varía muy poco mientras que las otras
variables termodinámicas estarán bien definidas a
medida que vayan cambiando. Los cambios serán
infinitesimales de manera que pueda invertirse la trayectoria
mediante un cambio diferencial en su medio
ambiente. Este proceso se denomina reversible.

Este caso no es solamente reversible sino también
isotérmico ya que suponemos una variación
infinitesimal (dT ).

También podríamos reducir el volumen
adiabáticamente sacando al cilindro de la fuente de calor.
Este proceso también puede ser reversible o irreversible
dependiendo de la manera en que movamos al émbolo. Pero
ΔU y ΔT no serαn los
mismos para los procesos
adiabáticos reversibles que para los
irreversibles.

4.10. Segunda Ley

Las primeras máquinas
térmicas construidas, fueron dispositivos muy eficientes.
Solo una pequeña fracción del calor absorbido de la
fuente de la alta temperatura se podía convertir en
trabajo útil. Aun al progresar los diseños de la
ingeniería, una fracción apreciable
del calor absorbido se sigue descargando en el escape de una
máquina a baja temperatura, sin que pueda convertirse en
energía mecánica. Sigue siendo una esperanza
diseñar una maquina que pueda tomar calor de un
depósito abundante, como el océano y convertirlo
íntegramente en un trabajo útil. Entonces no seria
necesario contar con una fuente de calor una temperatura
más alta que el medio ambiente
quemando combustibles. De la misma manera, podría
esperarse, que se diseñara un refrigerador que simplemente
transporte
calor, desde un cuerpo frío a un cuerpo caliente, sin que
tenga que gastarse trabajo exterior. Ninguna de estas
aspiraciones ambiciosas violan la primera ley de la
termodinámica. La máquina térmica
sólo podría convertir energía
calorífica completamente en energía
mecánica, conservándose la energía total del
proceso. En el refrigerador simplemente se transmitiría la
energía calorífica de un cuerpo frío a un
cuerpo caliente, sin que se perdiera la energía en el
proceso. Nunca se ha logrado ninguna de estas aspiraciones y hay
razones para que se crea que nunca se
alcanzarán.

La segunda ley de la termodinámica, que es una
generalización de la experiencia, es una exposición
cuyos artificios de aplicación no existen. Se tienen
muchos enunciados de la segunda ley, cada uno de los cuales hace
destacar un aspecto de ella, pero se puede demostrar que son
equivalentes entre sí. Clausius la enuncio como sigue: No
es posible para una máquina cíclica llevar
continuamente calor de un cuerpo a otro que esté a
temperatura más alta, sin que al mismo tiempo se produzca
otro efecto (de compensación). Este enunciado desecha la
posibilidad de nuestro ambicioso refrigerador, ya que éste
implica que para transmitir calor continuamente de un objeto
frío a un objeto caliente, es necesario proporcionar
trabajo de un agente exterior. Por nuestra experiencia sabemos
que cuando dos cuerpos se encuentran en contacto fluye calor del
cuerpo caliente al cuerpo frío. En este caso, la segunda
ley elimina la posibilidad de que la energía fluya del
cuerpo frío al cuerpo caliente y así determina la
dirección de la transmisión del calor. La
dirección se puede invertir solamente por medio de gasto
de un trabajo.

Kelvin (con Planck) enuncio la segunda ley con palabras
equivalentes a las siguientes: es completamente imposible
realizar una transformación cuyo único resultado
final sea el de cambiar en trabajo el calor extraído de
una fuente que se encuentre a la misma temperatura. Este
enunciado elimina nuestras ambiciones de la máquina
térmica, ya que implica que no podemos producir trabajo
mecánico sacando calor de un solo depósito, sin
devolver ninguna cantidad de calor a un depósito que
esté a una temperatura más baja.

Para demostrar que los dos enunciados son equivalentes,
necesitamos demostrar que si cualquiera de los enunciados es
falso, el otro también debe serlo. Supóngase que es
falso el enunciado de Clausius, de tal manera que se pudieran
tener un refrigerador que opere sin que se consuma el trabajo.
Podemos usar una máquina ordinaria para extraer calor de
un cuerpo caliente, con el objeto de hacer trabajo y devolver
parte del calor a un cuerpo frío.

Pero conectando nuestro refrigerador "perfecto" al
sistema, este calor se regresaría al cuerpo caliente, sin
gasto de trabajo, quedando así utilizable de nuevo para su
uso en una máquina térmica. De aquí que la
combinación de una maquina ordinaria y el refrigerador
"perfecto" formará una máquina térmica que
infringe el enunciado de Kelvin-Planck. O podemos invertir el
argumento. Si el enunciado Kelvin-Planck fuera incorrecto,
podríamos tener una máquina térmica que
sencillamente tome calor de una fuente y lo convierta por
completo en trabajo. Conectando esta máquina
térmica "perfecta" a un refrigerador ordinario, podemos
extraer calor de un cuerpo ordinario, podemos extraer calor de un
cuerpo caliente, convertirlo completamente en trabajo, usar este
trabajo para mover un refrigerador ordinario, extraer calor de un
cuerpo frío, y entregarlo con el trabajo convertido en
calor por el refrigerador, al cuerpo caliente. El resultado neto
es una transmisión de calor desde un cuerpo frío, a
un cuerpo caliente, sin gastar trabajo, lo infringe el enunciado
de Clausius.

La segunda ley nos dice que muchos procesos son
irreversibles. Por ejemplo, el enunciado de Clausius
específicamente elimina una inversión simple del proceso de
transmisión de calor de un cuerpo caliente, a un cuerpo
frío. Algunos procesos, no sólo no pueden
regresarse por sí mismos, sino que tampoco ninguna
combinación de procesos pueden anular el efecto de un
proceso irreversible, sin provocar otro cambio correspondiente en
otra parte.

4.11. Ciclos Termodinámicos

Todas las relaciones termodinámicas importantes
empleadas en ingeniería se derivan del primer y segundo
principios de
la termodinámica. Resulta útil tratar los procesos
termodinámicos basándose en ciclos: procesos que
devuelven un sistema a su estado original después de una
serie de fases, de manera que todas las variables
termodinámicas relevantes vuelven a tomar sus valores
originales. En un ciclo completo, la energía interna de un
sistema no puede cambiar, puesto que sólo depende de
dichas variables. Por tanto, el calor total neto transferido al
sistema debe ser igual al trabajo total neto realizado por el
sistema.

Un motor
térmico de eficiencia
perfecta realizaría un ciclo ideal en el que todo el calor
se convertiría en trabajo mecánico. El
científico francés del siglo XIX Sadi Carnot, que
concibió un ciclo termodinámico que constituye el
ciclo básico de todos los motores
térmicos, demostró que no puede existir ese
motor
perfecto. Cualquier motor térmico pierde parte del calor
suministrado. El segundo principio de la termodinámica
impone un límite superior a la eficiencia de un
motor, límite que siempre es menor del 100%. La eficiencia
límite se alcanza en lo que se conoce como ciclo de
Carnot.

Ciclo de Carnot: Es un ciclo
reversible que se representa en un diagrama p – v
(presión en función del volumen) que si bien tiene
sus limites en la capacidad que posee un sistema en convertir
calor en trabajo, es utilizado en máquinas
que usan vapor o una mezcla de combustible (con aire u
oxígeno).

a – b: El gas está en un estado de
equilibrio inicial representado por p1, V1,
T1 dentro del cilindro anteriormente descrito. Dejamos
que el gas se dilate lentamente hasta p2,
V2, T1. durante el proceso el gas absorbe
energía calórica Q1. La
dilatación es isotérmica a T1 y el gas
trabaja elevando al pistón y a su
carga.

<>

<>

Figura 17. Ciclo de
Carnot

b – c: Ponemos el cilindro sobre una base no
conductora y permitimos que el gas se dilate hasta
p3, V3, T2. La
dilatación es adiabática por que no entra ni sale
calor del sistema. El gas efectúa un trabajo elevando el
émbolo y su temperatura disminuye hasta
T2.

c – d: Ponemos el cilindro sobre un deposito de
calor (más frío) T2 y comprimimos el gas
lentamente hasta p4, V4,
T2. Durante ese proceso se transfiere una determinada
cantidad de energía calórica Q2 del gas
al depósito. La compresión es isotérmica a
T2 y se efectúa trabajo sobre el gas a
través del pistón y de su carga.

d – a: Ponemos al cilindro en un soporte no
conductor y comprimimos lentamente hasta su posición
inicial p1, V1, T1. La
compresión es adiabática, se efectúa trabajo
sobre el gas y su temperatura se eleva hasta
T1.

El trabajo neto W efectuado por el sistema durante el
ciclo está representado por el área encerrada en la
trayectoria abcd. La cantidad de energía calórica
neta recibida por el sistema se obtiene por la diferencia entre
Q2 y Q1.

Como el estado inicial y final es el mismo, no hay
cambio en la energía interna U del sistema. Por lo tanto,
según la primera ley de termodinámica:

W = Q1 –
Q2.

Eficiencia: es la relación entre el
trabajo total efectuado por una máquina en un ciclo y el
calor que, durante ese ciclo, se toma de la fuente de alta
temperatura.

e = W /Q1 =
(Q1-Q2)/Q1 =
1-Q2/Q1

Como dentro de un ciclo la cantidad de calor depende de
la temperatura (la masa se mantiene constante) también
podemos escribir:

e = 1 –
(T2/T1) ecc.40

4.12. Entropía

La entropía, como todas las variables de
estado, dependen sólo de los estados del sistema, y
debemos estar preparados para calcular el cambio en la entropía de procesos irreversibles,
conociendo sólo los estados de principio y al fin.
Consideraremos dos ejemplos:

1.- Dilatación libre: Dupliquemos el
volumen de un gas, haciendo que se dilate en un recipiente
vacío, puesto que no se efectúa reacción
alguna contra el vacío, W = 0 y, como el gas se encuentra
encerrado entre paredes no conductoras, Q = 0. por la primera ley
se entiende que

ΔU = 0 o:
Ui =
Uf

donde i y f se refieren a los estados
inicial y final (de equilibrio). Si el gas es ideal, U depende
únicamente de la temperatura y no de la presión o
el volumen, y la ecuación Ui =
Uf implica que Ti =
Tf.

En realidad, la dilatación libre es irreversible,
perdemos el control del medio
ambiente una
vez que abrimos la llave. Hay sin envergo, una diferencia de
entropía si – sf, entre los
estados de equilibrio inicial y final, pero no podemos calcularla
con la ecuación

ecc.41

, por que esta relación se aplica
únicamente a trayectorias reversibles; si tratamos de usar
la ecuación, tendremos inmediatamente la facultad de que
Q = 0 para la dilatación libre – además – no
sabremos como dar valores
significativos de T en los estados intermedios que no son
de equilibrio.

Entonces, ¿Cómo calcularemos
Sf – Si para estos estados?, lo
haremos determinando una trayectoria reversible (cualquier
trayectoria reversible) que conecte los estados i y
f, para así calcular el cambio de entropía
de la trayectoria. En la dilatación libre, un trayecto
reversible conveniente (suponiendo que se trate de un gas ideal)
es una dilatación isotérmica de VI a
Vf (=2Vi). Esto corresponde a la
dilatación isotérmica que se lleva a cabo entre los
puntos a y b del ciclo del Carnot.

Esto representa un grupo de
operaciones
muy diferentes de la dilatación libre y tienen en
común la única condición de que conectan el
mismo grupo de estados de equilibrio, i y f. De la
ecuación 41 y el ejemplo 1 tenemos.

Esto es positivo, de tal manera que la entropía
del sistema aumenta en este proceso adiabático
irreversible. Nótese que la dilatación libre es un
proceso que, en la naturaleza se desarrolla por sí mismo
una vez iniciado. Realmente no podemos concebir lo opuesto, una
compresión libre en la que el gas que en un recipiente
aislado se comprima en forma espontánea de tal manera que
ocupe solo la mitad del volumen que tiene disponible libremente.
Toda nuestra experiencia nos dice que el primer proceso es
inevitable y virtualmente, no se puede concebir el
segundo.

2.- Transmisión irreversible de calor.
Como otro ejemplo, considérense dos cuerpos que son
semejantes en todo, excepto que uno se encuentra a una
temperatura TH y el otro a la temperatura
TC, donde TH>
TC. Si ponemos ambos objetos en contacto dentro de
una caja con paredes no conductoras, eventualmente llegan a la
temperatura común Tm, con un valor entre
TH y TC; como la
dilatación libre, el proceso es irreversible, por que
perdemos el control del medio
ambiente, una vez que colocamos los dos cuerpos en la caja. Como
la dilatación libre, este proceso también es
adiabático (irreversible), por que no entra o sale calor
en el sistema durante el proceso.

Para calcular el cambio de entropía para el
sistema durante este proceso, de nuevo debemos encontrar un
proceso reversible que conecte los mismos estados inicial y final
y calcular el cambio de entropía, aplicando la
ecuación 41 al proceso. Podemos hacerlo, si imaginamos que
tenemos a nuestra disposición un deposito de calor de gran
capacidad calorífica, cuya temperatura T este bajo
nuestro control, digamos, haciendo girar una perilla. Primero
ajustamos, la temperatura del deposito a TH a
Tm, quitando calor al cuerpo caliente al mismo
tiempo. En este proceso el cuerpo caliente pierde
entropía, siendo el cambio de esta magnitud.

ΔSH
= – (Q/T1)

Aquí T1 es una temperatura
adecuada escogida entre TH y
Tm y Q es el calor
extraído.

En seguida ajustamos la temperatura de nuestro
depósito a Tc y lo colocamos en contacto
con el segundo cuerpo (el más frío). A
continuación elevamos lentamente (reversiblemente) la
temperatura del depósito de Tc a
Tm, cediendo calor al cuerpo frío
mientras lo hacemos. El cuerpo frío gana entropía
en este proceso, siendo su cambio

ΔSC = +
(Q/T2)

Aquí T2 es una temperatura
adecuada, escogida para que quede entre Tc y
Tm y Q es el calor agregado. El calor
Q agregado al cuerpo frío es igual al Q
extraído del cuerpo caliente.

Los dos cuerpos se encuentran ahora en la misma
temperatura Tm y el sistema se encuentra en el
estado de equilibrio final. El cambio de entropía para el
sistema completo es:

ecc.42

Como T1>T2, tenemos
Sf >Si. De nuevo, como para la
dilatación libre, la entropía del sistema aumenta
en este proceso reversible y adiabático.

Nótese que, como la dilatación libre,
nuestro ejemplo de la conducción del calor es un proceso
que en la naturaleza se desarrolla por sí mismo una vez
que se ha iniciado. En realidad no podemos concebir el proceso
opuesto, en el cual, por ejemplo, una varilla de metal en
equilibrio térmico a la temperatura del cuarto
espontáneamente se ajuste de tal manera, que un extremo
quede más caliente y en el otro más frío. De
nuevo, la naturaleza tiene la preferencia irresistible para que
el proceso se efectúe en una dirección determinada
y no en la opuesta.

En cada uno de estos ejemplos, debemos distinguir
cuidadosamente el proceso real (irreversible) (dilatación
libre o transmisión del calor) y el proceso reversible que
se introdujo, para que se pudiera calcular el cambio de
entropía en el proceso real.

Podemos escoger cualquier proceso reversible, mientras
conecte los mismos estados inicial y final que el proceso real;
todos estos procesos reversibles llevarán al mismo cambio
de entropía porque ella depende sólo los estados
inicial y final y no de los procesos que los conectan, tanto si
son reversibles como si son irreversibles.

Marcelo Tornería M.

Ingeniero Agrónomo

Especialista Riego y Drenaje