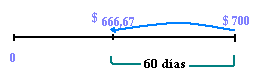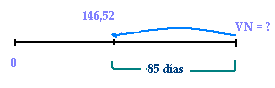Problemas resueltos de matemáticas financiera

Indice

2. Problemas de
Descuento
3. Transformación de
Tasas
4. Problemas de Interés
Compuesto
5. Problemas de Anualidades
Vencidas
6. Problemas de Anualidades
Anticipadas
7. Problemas de Anualidades
Diferidas
8. Problemas de Rentas
Perpetuas
9. Problemas de
Amortización
10. Problemas de Fondo de
Amortización
11.
Bibliografía

1. Problemas de
Interés
Simple

Formulas de Interés Simple

I = C * t * i

VF =C (1 + i * t)

C =VF (1 + i * t)-1

VF = C + I

I = interés; VF = valor futuro;
C = Capital; i =
tasa.

Calcular el interés
simple comercial de:

1. $2.500 durante 8 meses al 8%.

2. C = $2.500 t = 8 meses i= 0,08

   I = 2.500 * 8 * 0.08 =$133,33 Respuesta

   12

   I =$60.000 t =63 días i =0,09

   I =60.000 * 63 * 0.09=$ 945 Respuesta

   360

3. $60.000 durante 63 días al 9%.

   C =12.000 t =3 meses i =0,085

   I =12.000 * 3 * 0.085= $ 255 Respuesta

   12

4. $12.000 durante 3 meses al 8½ %.
5. $15.000 al 10% en el tiempo
   transcurrido entre el 4 de abril y el 18 de septiembre. Del
   mismo año.

C =$15.000 i =0,10 t =167 días

I =15.000 * 0.10 * 167=$ 695,83 Respuesta

360

Calcular el interés simple comercial
de:

1. $5.000 durante 3 años 2 meses 20 días
   al 0,75% mensual.

2. C = 5.000 i = 0,0075 t =116 meses

   3

   3años *12 meses =36 meses + 2 meses = 38
   meses + (20dias * 1 mes)= 116 meses

   1 año 30 días

   I =5.000 * 38,67 * 0,0075 =1.450
   Respuesta

   Nota: Fíjese que en este ejercicio la tasa
   esta expresa de en meses por lo que debe transformarse el
   tiempo también a meses

3. $8.000 durante 7 meses 15 días al 1,5%
   mensual.

C = $8000 t =7,5 i = 0,015

7 meses + 15 días * 1 mes =7,5 meses

30 días

I = 8.000 * 7.5 * 0,015=$900. Respuesta

2. Un señor pago $2.500,20 por un pagaré de $2.400, firmado el 10 de
   abril de 1996 a un con 41/2 %de interés. ¿En
   qué fecha lo pagó?

VF = 2.500,20

C =2.400

i = 0.045

t =?

VF = C (1 + i * t)

2.500,20 = 2400 (1 + 0,045 * t)

0,04175=0,045 t

t = 0,9277 años Respuesta 10 de marzo de 1997

Un inversionista recibió un pagaré por
valor de $120.000 a un interés del 8% el 15 de julio con
vencimiento a 150 días. El 200de octubre del mismo
maño lo ofrece a otro inversionista que desea ganar el
10%. ¿Cuánto recibe por el pagaré el primer
inversionista?

VF =120.000(1 + 0,08 * 150) =124.000

360

124.000(1 + 0,1 * 53)-1= 122.000,93
Respuesta

360

Una persona debe
cancelar $14.000 a 3 meses, con el 8% de interés. Si el
pagará tiene como cláusula penal que, en caso de
mora, se cobre el 10%
por el tiempo que exceda al plazo fijado ¿qué
cantidad paga el deudor, 70 días después del
vencimiento?

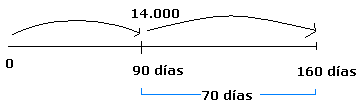
VF = 14.000(1 + 0,08 * 3) = 14.280 Valor de
vencimiento

12

VF = 14.280(1+0,1 * 70) =14.557,67 respuesta – valor de
mora.

360

Una persona descuenta el 15 de mayo un pagaré de
$ 20.000 con vencimiento para el 13 de agosto y recibe &
19.559,90. ¿A qué tasa de descuento racional o
matemático se le descontó el
pagaré?

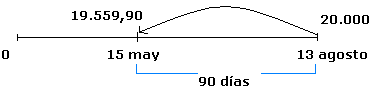
VF =VP (1+ i * t)

20.000=19.559,90 (1 + i * 90)

360

i =0, 09 è 9% Respuesta

Una persona debe $20.000 con vencimiento a 3 meses y
$16.000 con vencimiento a 8 meses. Propone pagar su deuda
mediante dos pagos iguales con vencimiento a 6 meses y un
año, respectivamente. Determine el valor de los nuevos
pagarás al 8% de rendimiento (tómese como fecha
focal dentro de un año).

Vf1=20.000(1+0,08 * 9)= 21.200

12

Vf2=16.000(1+0,08 * 4)= 16.426,67

12

Deuda = 21.200 + 16.426,67

Deuda = 37.626,67

Pagos

P1 = x (1+0,08 * 6) =1,04 x

12

P2 = x

Pagos =P1 +P2

Pagos =2,04 x

Deuda = Pagos

37.626,67=2,04 x

Valor de los pagarés 18.444,45 cada uno
/Respuesta

Nota: En este problema como en todos los similares debe
llevarse los valores de las
deudas a la fecha focal, en este caso 12 meses, para poder
efectuar operaciones sobre
estos valores.

2. Problemas de
Descuento

Formulas para Descuento Real

D = VP * t * d

VN= VP + D

VN = VP (1 + d* t)

VP = VN (1 + d * t)-1

Las formulas son iguales a las de interés simple
he aquí sus equivalencias.

i = d tanto por ciento/tasa de descuento

I = D descuento

VF =VN valor nominal

C =VP valor presente

Formulas de Descuento Comercial

D = VP * t * d

VN= VP + D

VN = VP (1 + d* t)

VP = VN (1 – d * t)

Determinar el valor líquido de los
pagarés, descontados en un banco a las tasas
y fechas indicadas a continuación:

a. $20.000 descontados al 10%, 45 días de su
vencimiento.

20.000(1- 0.1 * 45)= 19.750 Respuesta

360

b. $18.000 descontados al 9%, 2 meses antes de su
vencimiento.

18.000(1-0.09 * 2)=17.730 Respuesta

12

c. $14.000 descontados al 8% el 15 de junio, si su fecha
de vencimiento es para el 18 de septiembre del mismo
año.

14.000(1-0.08 * 95)=13.704,44 Respuesta

360

d. $10.000 descontados al 10% el 20 de noviembre,
si su fecha de vencimiento es para el 14 de febrero del
año siguiente.

10.000(1-0.1 * 86)=9.761,11 Respuesta

360

2.2. Alguien vende una propiedad por
la que recibe los siguientes valores el 9 de julio de cierto
año:

a. $20.00 de contado

b. Un pagaré por $20.000, con vencimiento el 9 de
octubre del mismo año.

c. Un pagaré por $30.000, con vencimiento el 9 de
diciembre del mismo año.

Si la tasa de descuento bancario en la localidad es del
9%, calcular el valor real de la venta.

a. 20.000 contado

b. 20.000(1-0.09 * 92)=19.540

360

1. 360 Total =20.000 + 19.540 + 28.852,5 = $68.392,50
   Respuesta

   Un pagaré de $10.000 se descuentan al 10% y
   se reciben del banco $9.789. Calcular la fecha de
   vencimiento del pagaré.

   10.000=9.789 (1+0.1 * t)

   t = 0,21 años

   0,21 años * 12 meses = 2,52 meses
   Respuesta

   1 año

   El Banco Ganadero descuenta un pagaré por
   $80.000 al 10%, 90 días antes de su vencimiento, 5
   días después lo redescuenta en otro banco a la
   tasa del 9%. Calcular la utilidad del
   Banco Ganadero.

   80.000(1-0.1 * 90)=78.000

   360

   80.000(1-0.09 * 75)= 78.500

   360

   Utilidad 78.500-78.000= 500 Respuesta

   ¿Qué tasa de descuento real se aplico
   a un documento con valor nominal de 700 dólares, si se
   descontó a 60 días antes de su vencimiento y se
   recibieron 666,67 dólares netos?

   

   700=666,67(1 + i 60)

   360

   i = 0.30 è 30% Respuesta

   ¿Cuál es el valor nominal de un
   pagaré por el cual se recibieron 146,52
   dólares, si se descontó comercialmente a un
   tipo de 49%, 85 días antes de su
   vencimiento?

   

   146,52 = VF (1 – 0,49 * 85)

   360

   VF = 165,68 Respuesta.

   3.
   Transformación de Tasas

   Método de igualación

   Del 18% efectivo trimestral encuentre la tasa
   nominal trimestral capitalizable mensualmente

   (1+ 0,18)4/12 = (1 +
   ntnm)12/12

   3

   T. nominal trimestral capitalizable mensualmente =
   0, 17 è
   17,01% R.

   Del 24% nominal anual capitalizable anualmente,
   encuentre la tasa nominal trimestral capitalizable
   semestralmente.

   (1+ 0,24)1/2 = (1 + ntcs *
   2)2/2

   Tasa nominal trimestral capitalizable semestralmente
   =5,6 % Respuesta.

   Del 12% nominal anual capitalizable trimestralmente,
   encuentre la tasa nominal semestral capitalizable
   trimestralmente.

   (1+ 0,12)4/4 = (1 +
   nsct)4/4

   4 2

   Tasa nominal semestral capitalizable trimestralmente
   =0,06 è
   6% R.

   Del 22% efectivo semestral, encuentre la tasa
   efectiva bimensual.

   (1+ 0,22)2/6 = (1 + e
   b)6/6

   Tasa efectiva bimensual = 0,06852 è 6,85%
   Respuesta.

   Del 30% nominal bimensual capitalizable
   semestralmente, encuentre la tasa nominal trimestral
   capitalizable anualmente.

   (1+ 0,30 * 3)2 = (1 + ntca)

   3

   Tasa nominal trimestral capitalizable anualmente =
   0,6525 è
   65,25% R.

   Del 52% nominal anual capitalizable anualmente,
   encuentre la tasa nominal trimestral capitalizable
   semestralmente.

   (1+ 0,52)1/2 = (1 + ntcs *
   2)2/2

   Tasa nominal capitalizable semestralmente =
   0,1164 è
   11,54% Resp.

   4. Problemas de
   Interés Compuesto

   Formulas de Interés
   Compuesto:

   M = C (1 + i)n

   C = M (1 + i)-n

   M = monto o también llamado VF; C = capital;
   i = tasa; n =tiempo

   Hallar la cantidad que es necesario colocar en una
   cuenta que paga el 15% con capitalización trimestral,
   para dispones de 20.000 al cabo de 10
   años.

   i = 0,15 efectiva trimestral

   n = 10 años

   M = 20.000

   C =?

   C = 20.000 (1+ 0.15)-10(4)

   4

   C =4.586,75 Respuesta

   ¿Cuántos meses deberá dejarse
   una póliza de acumulación de $2.000 que paga
   el 3% anual, para que se convierta en %7.500?

   n =?

   C = 2.000

   i = 0,03

   M =7.500

   7.500 = 2.000 (1 +0,03)n

   ln 15/4 = n ln 1,03

   n = 44,71 años

   44,71 años * 12 meses = 536,52 meses
   Respuesta.

   1 año

   Hallar el valor futuro a interés compuesto de
   $100, para 10 años:

   a. al 5% efectivo anual

   M = 100 (1 + 0,05)10 = 162,89
   Respuesta

   b. al 5% capitalizable mensualmente

   M = 100 (1 + 0,05)10(12) =164,20
   Respuesta

   12

   c. al 5% capitalizable trimestralmente

   M = 100 (1 + 0,05)10(4) =164,36
   Respuesta

   4

2. 30.000(1-0.09 * 153)=28.852,5
3. al 5% capitalizable semestralmente

M = 100 (1 + 0,05)10(2) =164,86
Respuesta

2

Hallar el valor futuro de $20.000 depositados al 8%,
capitalizable anualmente durante 10 años 4
meses.

VF = 20.000(1 + 0,08) 10 (4/12) = 44.300,52
Respuesta

¿Qué tasa capitalizable semestralmente es
equivalente al 8%, capitalizable trimestralmente?

(1+ 0,08)4/2 = (1 +
n.c.s)2/2

4 2

i =0,0808 è 8,08% Respuesta

Hallar la tasa nominal convertible semestralmente, a la
cual $10.000 se convierten en $12.500, en 5
años.

12.500 = 10.000 (1 +i )10

2

i =0,0451 è 4,51% Respuesta

¿Cuántos años deberá dejarse
un depósito de $6.000 en una cuenta de ahorros que acumula
el 8% semestral, para que se conviertan en $10.000?

10.000=6.000 (1+ 0,08)n

n = 13,024 /2

n = 6,512 años Respuesta

¿Qué es más conveniente: invertir
en una sociedad maderera
que garantiza duplicar el capital invertido cada 10 años,
o depositar en una cuenta de ahorros que ofrece el 6%
capitalizable trimestralmente?

M =2

C = 1

2=1(1+ i) 10

i = 7,17% sociedad maderera

————–

M = 1(1+0,06)

4

M =1,8140 no duplico

Respuesta es más conveniente la sociedad
maderera

Una inversionista ofreció comprar un
pagará de $120.000 sin interés que vence dentro de
3 años, a un precio que le
produzca el 8% efectivo anual; calcular el precio
ofrecido.

C = 120.000(1 + 0,08)-3

C = 95.259,87 Respuesta

Hallar el VF a interés compuesto de $20.000 en 10
años, a la tasa del 5% de interés. Comparar el
resultado con el monto compuesto al 5%, convertible
mensualmente.

VF = 20.000(1 + 0,05) 10 = 32.577,89
Respuesta

VF = 20.000(1 + 0,05) 120 = 32.940,19
convertible mensualmente Resp.

12

5. Problemas de Anualidades
Vencidas

Formulas de Anualidades Vencidas

F = A [¨ (1 + i )n -1] =Valor
futuro

i

P = A [¨ 1 – (1+ i )-n ]=Valor
presente

i

F = Valor futuro; A = anualidad; n = tiempo

Calcular el valor futuro y el valor presente de las
siguientes anualidades ciertas ordinarias.

(a) $2.000 semestrales durante 8 ½ años al
8%, capitalizable semestralmente.

F = 2.000[¨ (1 + 0, 04)17 -1] =47.395,07
valor futuro

0,04

P = 2.000[¨ 1 – (1+ 0, 04)-17
]=24.331,34 valor presente

0,04

(b) $4.000 anuales durante 6 años al 7,3%,
capitalizable anualmente.

F = 4.000[¨ (1 + 0, 073)6 -1] =28.830,35
valor futuro

0,073

P = 4.000[¨ 1 – (1+ 0, 073)-6
]=18.890,85 valor presente

0,073

(c) $200 mensuales durante 3 años 4 meses, al 8%
con capitalización mensual.

F = 200[¨ (1 + 0, 0067)40 -1] =9.133,50
valor futuro

0,0067

P = 200[¨ 1 – (1+ 0, 0067)-40
]=7.001,81 valor presente

0,0067

Calcular el valor de contado de una propiedad vendida en
las siguientes condiciones: $20.000 de contado; $1.000 por
mensualidades vencidas durante 2 años y 6 meses y un
último pago de $2.500 un mes después de pagada la
última mensualidad. Para el cálculo,
utilizar el 9% con capitalización mensual.

i =0,09/12=0,0075

P = 1.000[¨ 1 – (1+ 0, 0075)-30
]=26.775,08

0,0075

2.500(1+0,0075)-31=1.983,09

26.775,08 + 1.983,09 + 20.000 = 48.758,17
Respuesta.

¿Cuál es el valor de contado de un equipo
comprado con el siguiente plan: $14.000 de
cuota inicial; $1.600 mensuales durante 2 años 6 meses
con un último pago de $2.500, si se carga el 12% con
capitalización mensual?

i =0,12/12=0,01

P = 1.600[¨ 1 – (1+ 0, 01)-30
]=41.292,33

0,01

2.500(1+0,01)-31=1.836,44

41.292,33 + 1.836,44 + 14.000 = 57.128,78
Respuesta

Una mina en explotación tiene una producción anual de $8’000.000 y se
estima que se agotará en 10 años. Hallar el valor
presente de la producción, si el rendimiento del dinero es del
8%.

P = 8.000.000[¨ 1 – (1+ 0, 08)-10
]=53.680.651,19 respuesta.

0,08

En el ejercicio 5.4. Se estima que al agotarse la mina
habrá activos
recuperables por el valor de $1’500.000. Encontrar el
valor presente, incluidas las utilidades, si estas representan
el 25% de la producción.

1.500.000(1 + 0,08)-10 = 694.790,
23

53.680.651,19 * 0,25 =13.420.162,8

694.790,23 + 13420.162,80 = 14.114.953,03
Respuesta

En el momento de nacer su hija, un señor
depositó $1.500 en una cuenta que abona el 8%; dicha
cantidad la consigna cada cumpleaños. Al cumplir 12
años, aumento sus consignaciones a $3.000. Calcular la
suma que tendrá a disposición de ella a los 18
años.

F = 1.500 [¨ (1 + 0, 08)11 -1]
=24.968,23

0,08

24.968,23(1 + 0,08)7 =42.791,16

F = 3.000[¨ (1 + 0, 08)7 -1]
=26.768,41

0,08

1.500(1 + 0,08)18= 5994,02

42.791,16 + 26.768,41 + 5994,02 = 75.553,60
Respuesta

Una persona deposita $100 al final de cada mes en una
cuenta que abona el 6% de interés, capitalizable
mensualmente. Calcular su saldo en la cuenta, al cabo de 20
años.

0,06 /12 =0,005 tasa mensual

F = 100[¨ (1 + 0, 005)240 -1] =46.204,09
Respuesta.

0,005

6. Problemas de
Anualidades Anticipadas

Formulas de Anualidades Anticipadas

F = A [¨ (1 + i )n + 1 -1 – 1] =Valor
futuro

i

P = A [¨1 + 1 – (1+ i )-n +
1]=Valor presente

i

F = Valor futuro; A = anualidad; n = tiempo

Calcular el valor de Contado de una propiedad vendida a
15 años de plazo, con pagos de $3.000 mensuales por mes
anticipado, si la tasa de
interés es del 12% convertible
mensualmente.

P = 3.000 [¨1 + 1 – (1+ 0,01 )-180 +
1]= 252.464,64

0,01

Una persona recibe tres ofertas parea la compra de su
propiedad: (a) $400.000 de contado; (b) $190.000 de contado y
$50.000 semestrales, durante 2 ½ años (c) $20.000
por trimestre anticipado durante 3 años y un pago de
$250.000, al finalizar el cuarto año. ¿Qué
oferta debe
escoger si la tasa de interés es del 8% anual?

Oferta b

P = 50.000 [¨1 + 1 – (1+ 0,04 )-4]=
231.494,76 + 190.000 = 421.494,76

0,04

Oferta c

P =20.000 [¨1 + 1 – (1+ 0,02 )-11]=
215.736,96

0,02

25.000(1 +0,08)-4 = 183.757,46

215.736,96 + 183.757,46 = 399.494,42

Respuesta = Oferta b es la más
conveniente.

¿Cuál es el valor presente de una renta de
$500 depositada a principio de cada mes, durante 15 años
en una cuenta de ahorros que gana el 9%, convertible
mensualmente?

P =500 [¨1 + 1 – (1+ 0,0075 )-179]=
49.666,42 Respuesta.

0,0075

¿Qué suma debe depositarse a principio de
cada año, en un fondo que abona el 6% para proveer la
sustitución de los equipos de una compañía
cuyo costo es de
$2.000.000 y con una vida útil de 5 años, si el
valor de salvamento se estima en el 10% del costo?

2’000.000 * 0.10= 200.000

2’000.000 – 200.000 = 1’800.000

1´800.000 = A [¨ (1 + 0,06 )6 -1 –
1]

0,06

A = 301.239,17 Respuesta.

Sustituir una serie de pagos de $8.000 al final de cada
año, por el equivalente en pagos mensuales anticipados,
con un interés del 9% convertible mensualmente.

8.000 = A [¨ (1 + 0,0075 )13 -1 –
1]

0,0075

A = 634,85 Respuesta.

Un empleado consigna $300 al principio de cada mes en
una cuenta de ahorros que paga el 8%, convertible mensualmente.
¿En cuánto tiempo logrará ahorrar
$30.000?

0,08 = 0,0067

12

30.000 = 300 [¨ (1 + 0,08 )n + 1 -1 –
1]

0,08

n = 76,479 meses

7. Problemas de
Anualidades Diferidas

Formulas para anualidades diferidas

Son las mismas que las anualidades vencidas y
anticipadas salvo que estas tienen un periodo de
gracia.

Una compañía adquiere unos yacimientos de
mineral; los estudios de ingeniería muestran que los trabajos
preparatorios y vías de acceso demoraran 6 años. Se
estima que los yacimientos en explotación rendirán
una ganancia anual de $2.400.000. suponiendo que la tasa
comercial es del 8% y que los yacimientos se agotarán
después de 15 años continuos de explotación,
hállese el valor futuro de la renta que espera
obtenerse.

VF = 2.400.000 [(1 + 0,08)15 – 1]

0,08

VF = 6.516.503,43 Respuesta

En el problema anterior, hállese el valor de
utilidad que espera obtener, en el momento de la
adquisición de los yacimientos.

VP = 2.400.000 [1 – (1 + 0,08)-15
]

0,08

VP = 20.542.748,85

20.542.748,85 (1 + 0,08)-6 = 12.945.416
Respuesta.

Una compañía frutera sembró
cítricos que empezaran a producir dentro de 5 años.
La producción anual se estima en $400.000 y ese
rendimiento se mantendrá por espacio de 20 años.
Hallar con la tasas del 6% el valor presente de la
producción.

VP = 400.000 [1 – (1 + 0,06)-20 ]

0,06

VP = 4587968,487 (1 + 0,06)-5 =
3428396,90

Alguien deposita $100.000 en un banco, con la
intención de que dentro de 10 años se pague, a
él o a sus herederos, una renta de $2.500, a principio de
cada mes. ¿Durante cuántos años se
pagará esta renta, si el banco abona el 6% convertible
mensualmente?

VF = 100.000 (1 + 0,005)120 =
181.939,67

181939,67 = 2.500 [ 1 + 1- (1 + 0,005)-n +1
]

0,005

n = 90,13

Respuesta = 7 años 7meses

Una deuda contraída al 8% nominal, debe
cancelarse con 8 cuotas semestrales de $20.000 c/u, con la
primera obligación por pagar dentro de 2 años.
Sustituirla por una obligación equivalente pagadera con 24
cuotas trimestrales, pagándose la primera de
inmediato.

20.000 [1 + 1 – (1 + 0,04)-7 ] (1+0,04)-4 =
119.707,7136

0,04

119.707,71 = A [1 + 1 – (1 +
0,02)-23]

0,02

A = 6.204,97 Respuesta anualidades
trimestrales

8. Problemas de Rentas
Perpetuas

Formulas de Rentas Perpetuas

P = A

i

P = A + A

i

CC= Co + Com

i

P = perpetuidad; A = anualidad; Co = costo inicial; CC =
costo capitalizado;

i = interés

Hallar el valor actual de una perpetuidad de $5.000,
cuyo primer pago se hará dentro de 6 meses, con tasa
nominal del 12% convertible mensualmente

P =5.000=500.000

0,01

M =500.000(1 + 0,01)-5 = 475.732,84
Respuesta.

Hallar el valor actual de una renta de $156.000 por
año vencido, suponiendo un interés de:

a. 6% efectivo

156.000 = 2’561.576,35 Respuesta

0,06

b. 6% convertible semestralmente

156.000 = A [(1 + 0,03)2 – 1]

0,03

A = 76.847,29

P =76.847,29=2’561.576,35 Respuesta

0,03

c. 6% convertible mensualmente.

156.000 = A [(1 + 0,005)12 – 1]

0,005

A = 12.646,36

P =12.646,36=2’529.272,61 Respuesta

0,005

Los exalumnos de una universidad
deciden donarle un laboratorio y
los fondos para su mantenimiento
futuro. Si el costo inicial de $200.000 y el mantenimiento se
estima en $35.000 anuales, hallar el valor de la
donación, si la tasa efectiva es del 7%.

P = 200.000 + 35.000 = 700.000 Respuesta

0,07

Para mantener en buen estado las
carreteras vecinales, la junta vecinal decide establecer un
fondo a fin de proveer las reparaciones futuras, que se estiman
en $300.000 cada 5 años. Hallar el valor del fondo, con
la tasa efectiva del 6%.

300.000 = A [(1 + 0,06)5 – 1]

0,06

A = 53.218,92

P = 53.218,92 = 886.982 Respuesta

0,06

Calcular el costo capitalizado de un equipo industrial
que cuesta $800.000 y tiene una vida útil de 12
años, al final de los cuales debe remplazarse, con el
mismo costo. Calcular con la tasa del 6%.

800.000 = A [(1 + 0,06)12 – 1]

0,06

A = 47.421,62

CC = 800.000 + 47421,62

0,06

CC = 1’590.360,39 Respuesta.

En el problema anterior, calcular el costo capitalizado,
suponiendo un valor de salvamento igual al 15% del costo
original.

800.000 * 0.15 =120.000

680.000 = A [(1 + 0,06)12 – 1]

0,06

A = 40.308,38

CC = 800.000 + 40.308,37

0,06

CC = 1’471.806,33 Respuesta

Una industria
recibe dos ofertas de cierto tipo de máquina, ambas de
igual rendimiento. La primer oferta es por $380.000 y las
maquinas tiene una vida útil de 7 años; la segunda
oferta es de $510.000 por maquinas que tienen una vida
útil de 10 años. Si el precio del dinero es el 6%
efectivo, ¿qué oferta es más
conveniente?

Primera oferta

380.000 = A [(1 + 0,06)7 – 1]

0,06

A = 45.271,30

CC = 380.000 + 45.271,30

0,06

CC = 1’134.521,78 Respuesta

Segunda Oferta

510.000 = A [(1 + 0,06)10 – 1]

0,06

A = 38692,66

CC = 510.000 + 38.692,66

0,06

CC = 1’154.877,65 Respuesta

Respuesta = El CC de la primera oferta en menor en
20.355,86

9. Problemas de
Amortización

Formulas para anualidades diferidas

F = A [¨ (1 + i )n -1] =Valor
futuro

i

P = A [¨ 1 – (1+ i )-n ] =Valor
presente

i

F = Valor futuro; A = anualidad; n = tiempo

Nota: Son las mismas que las anualidades vencidas y
anticipadas.

1. Una deuda de $20.000 debe amortizarse con 12 pagos
   mensuales vencidos. Hallar el valor de estos, a la tasa
   efectiva del 8%, y elaborar el cuadro de amortización para los dos primeros
   meses.

(1+0,08)1/12 = (1+
e.m)12/12

i = 6,43 *10-3

20.000= A [ 1 – (1 + 0,0064)-12 ]

0,0064

A = 1.737,19 Respuesta

Una deuda de $100.000 debe cancelarse con pagos
trimestrales vencidos en 18 cuotas, con interés del 12%
capitalizable semestralmente. Hallar el saldo insoluto, al
efectuar el noveno pago.

(1+0,12)2/4 = (1
+et)4/4

100.000 = A [ 1 – (1 + 0,029)-18 ]

0,029

A = 7.244,03 Anualidad

Para encontrar el valor del noveno pago

F = 7.244,03 [ (1 + 0,029)-9 – 1 ]

0,029

F = 73.462,00

M = 100.000 (1 + 0,029)9 =
129.979,95

73.462,00 + 129.979,95 = 56.517,95 Respuesta Saldo
insoluto al noveno pago.

Una propiedad se vende en $300.000, pagaderos
así; $100.000 al contado y el saldo en 8 cuotas iguales
semestrales con interés del 10% convertible
semestralmente. Hallar los derechos del vendedor y del
comprador, al efectuarse el quinto pago

300.000 – 100.000 = 200.000

200.000 = A [ 1 – (1 + 0,05)-8 ]

0,05

A = 30.944,36

F = 30.944,36 [ (1 + 0,05)-5 – 1 ]

0,05

F = 170.987,13

M = 200.000 (1 + 0,05)5 =
255.256,31

Derecho del Vendedor 255.256,31 -170.987,13 =
84.269,17

D. comprador + 84.269,17 = 300.000

D comprador = 215.730.83

¿Con cuantos pagos semestrales iguales y vencidos
de $9.500 se pagaría la adquisición de un terreno
que cuesta $29.540 si se carga una tasa anual de 34% convertible
mensualmente?

Conversión de la tasa

(1 +0,34)6 = (1 +i.s.)

12

Interés semestral = 0,1825

29.540 = 9.500 [ 1 – (1 + 0,1825)-n
]

0,1825

ln 0,4325 = – n ln(1,1825)

-0,838 = -n (0,1676)

n = 5 pagos semestrales Respuesta

Determine el número de pagos necesarios para
amortizar totalmente la compra a crédito
de un automóvil que cuesta $48.000 y se vende con un
enganche de 45% y el resto a pagar en mensualidades vencidas de
$1.254,75 con interés al 39% convertible
mensualmente.

Enganche 21.600

Quedan 26.400

i = 0,39

12

i = 0,0325

26.400 = 1254,75 [ 1 – (1 + 0,0325)-n
]

0,0325

n = 36 mensualidades Respuesta

Una aspiradora se vende en $499 al contado o mediante 4
pagos mensuales anticipados de $135 ¿Cuál es la
tasa efectiva mensual que se paga al adquirir ese aparato a
crédito?

499 = 135 [1 + 1 – (1 +
i)-3]

i

2,69 = 1 – (1 + i)-3

i

Interpolación

0,06 – 0,05 = 0,06 – i

2,6730 – 2,7232 2,6730 – 2,69

0,00017 = 0.06 – i

0,0502

i = 0,05661

i = 5,66 % Respuesta

10. Problemas de
Fondo de Amortización

Formulas para anualidades diferidas

F = A [¨ (1 + i )n -1] =Valor
futuro

P = A [¨ 1 – (1+ i )-n] =Valor
presente

i

F = Valor futuro; A = anualidad; n = tiempo

Nota: Son las mismas que las anualidades vencidas y
anticipadas.

1. Se establece un fondo de $5.000 semestrales que
   abona el 6% capitalizable semestralmente. Hallar el valor
   acumulado en 5 años y elaborar el cuadro del
   fondo.

0,06 = 0,03

2

F = 5.000 [¨ (1 + 0,03 )10 -1]
=57.319,39

0,03

Un artesano necesita remplazar cada 5 años todas
sus herramientas,
cuyo valor es de $10.000. ¿Qué deposito mensual
debe hacer en una cuenta de ahorros que abona el 8%,
capitalizable trimestralmente?

(1 + 0,08)4/12= (1 +
e.m)12/12

4

Tasa efectiva mensual = 6,622 *
10-3

10.000 = A [(1 + 6,622 * 10-3)2 –
1]

6,622 * 10-3

A = 136,28 Respuesta

Para cancelar una deuda de $80.000 a 5 años
plazos, se establecen reservas anuales en un fondo que abona el
6%; transcurridos dos años eleva sus intereses al 7%.
Hallar las reservas anuales y hacer el cuadro de fondo

80.000 = A [(1 + 0,06)5 – 1]

0,06

A = 14.191,71 Primeros dos años

F = 14.191,71 [¨ (1 + 0,06)2 -1] =
29.234,92

0,06

M = 29234,92 (1+ 0,07)3 = 35.814,04

44.185,95 = A [(1 + 0,07)3 – 1]

0,07

A = 13.744,11 Los 3 últimos
años.

Un municipio emite obligaciones a
10 años de plazo por $2.000.000 que devengan el 8% de
interés. ¿Qué depósitos anuales debe
hacer en un fondo que abona el 6% y que egreso anual
tendrá el municipio hasta el pago de la deuda?

2.000.000 * 0,08 = 160.000

2.000.000 = A [¨ (1 + 0,06)10
-1]

0,06

A = 151.735,92 depósitos anuales

151.735,92 + 160.000 = 311735,92 Respuesta total egreso
anual

Hallar la reserva anual en un fondo que paga el 7% de
interés, para cancelar en 25 años una deuda de
$100.000.

100.000 = A [¨ (1 + 0,07)25
-1]

0,07

A = 1.518,05 depósitos anuales

Se deben pagar $29.000 dentro de 12 meses por una deuda
con anterioridad. Si para pagarla se decide constituir un fondo
mediante depósitos bimestrales vencidos
¿cuál sería el importante de los mismos si
se colocan en un instrumento de inversión que rinde el 26% convertible
mensualmente?

(1 + 0,26)12/6 = (1 + i.
bimestral)6/6

12

i = 0,04380

29.000 = A [¨ (1 + 0,04380)6
-1]

0,04380

A = 4330,4922 Respuesta.

Para pagar una deuda de $5.400 que vence dentro de 5
meses se va a construir un fondo mediante depósitos
mensuales anticipados. Si los depósitos se colocan en un
fondo de inversiones
que rinde el 32% anual convertible mensualmente, hallar su
importe.

i = 0,32

12

i = 0,0266

5.400= A [¨ (1 + 0,0266)6 -1 –
1]

0,0266

A = 997,32 Respuesta.

Haga una tabla que muestre la forma en que
amortizaría una deuda de $15.000 contratada hoy y que debe
pagarse en 3 meses con interés al 12% trimestral
capitalizable mensualmente si se decide constituir un fondo
mediante depósitos quincenales vencidos en una cuenta de
inversiones que rinde el 2,7% mensual efectivo.

(1 + 0,027)12/24 = (1 +e.
q.)24/24

Efectiva quincenal = 0,0134

16.872,96 = A [¨ (1 + 0,0134)6
-1]

0,0134

A = 2719,34677 Respuesta.

¿Cuál debe ser el importe de cada uno de 8
depósitos mensuales anticipados que se colocan en un fondo
de inversión que rinde el 28,4% convertible mensualmente
con el objeto de amortizar una deuda de $8.888,89 que vence
exactamente dentro de 8 meses?

8.888,89 =A [¨ (1 + 0,02375)9 -1 –
1]

0,02375

A = 998,29 Respuesta

11.
Bibliografía

• Alfredo Díaz Mata – Víctor Manuel
  Aguilera G. Matemáticas Financiera. Segunda
  Edición. Editorial Mc. Graw Hill. Ejercicios Propuestos.
  1.998
• Lincoyan Protus G. Matemáticas Financiera.
  Cuarta Edición. Editorial Mc Graw Hill. Cuarta
  Edición. Ejercicios Propuestos. 1.997

Autor:

Ena Maria Vera Espinoza