
TEOREMA DEL MUESTREO
El teorema de muestreo fue desarrollado en 1928 por Nyquist Shannon y probado matemáticamente por Claude Shannon en 1949.

¿Qué es el muestreo?
Es la conversión de una señal en tiempo continuo a una señal en tiempo discreto. Se obtiene tomando muestras periódicas de esa señal continua cada T segundos.

Muestreo Periódico
X(n) = Xa(nT)
Donde X(n) es la señal en tiempo discreto obtenida de las muestras hechas a la señal analógica Xa(t) cada T segundos.
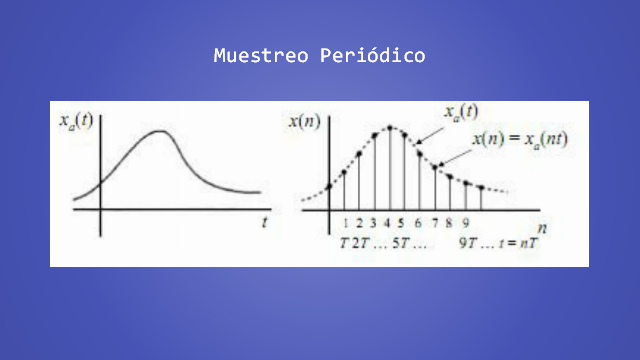
Muestreo Periódico

Muestreo Periódico
El muestreo periódico establece una relación entre las variables t de tiempo continuo y n de tiempo discreto mediante:
t= nT= n/T (Velocidad de muestreo)
Se considera una señal analógica de la siguiente forma
Xa(t) = Acos(2pFt + T)
Cuando se muestrea periódicamente a una velocidad de Fs = 1/T muestras por segundo, queda de la siguiente forma:
X(n) = Acos((2pnF / Fs) + T)

Muestreo Periódico
Ejemplo:
Se considera la siguiente señal analógica:
Xa(t) = 3cos(100p t)
a) Si la señal de muestrea a una velocidad de Fs = 200 Hz. ¿Cuál es la señal de tiempo discreto obtenidas tras el muestreo?
b) Si la velocidad de muestreo cambia a Fs= 75 Hz.
a) X(n) = 3cos((100 p / 200) * n)

Antecedentes Históricos

Teorema del Muestreo
Según algunos autores, los orígenes de la teoría del muestreo pueden rastrearse hasta el trabajo de Cauchy, Borel, Lagrange, Laplace y Fourier, si no más atrás. Como muchos otros teoremas fundamentales, fue desarrollado gradualmente por varios científicos, y no es sencillo determinar la fecha exacta de su aparición

Harry Nyquist

Claude E. Shannon

Otros Descubridores
Vladimir A. Kotelnikov-1933
Edmund Taylor Whittaker-1915
John Macnaghten Whittaker-1935
Dennis Gabor-1946

Teorema del muestreo
Higgins (1985) resalta que el teorema del muestreo debe en realidad considerarse en dos partes:
la primera donde se demuestra que es posible recuperar exactamente una señal de ancho de banda limitada a partir de sus muestras;
la segunda, que describe cómo reconstruir la función utilizando estas muestras (problema de interpolación)

Cronología de trabajos sobre teorema del muestreo

Porque se llamo teorema de muestreo de Nyquist
El término teorema de muestreo de Nyquist apareció en 1959 en un libro de su ex empleador, Bell Labs, y apareció de nuevo en 1963.

Algunos Casos Reales
En un CD (Compact Disk) de audio, la frecuencia de muestreo es de 44.100 muestras/segundo. Esto significa que la máxima componente de frecuencia representada es igual a 22.050 Hz.
En un SuperAudio CD, la frecuencia de muestreo es igual a 2.822 MHz.
En el sistema Dolby Digital las frecuencias de muestreo son de 32 kHz, 44.1 kHz y 48 kHz
En el sistema DTS (Digital Theather System) las frecuencias de muestreo son 32 kHz, 44.1 kHz, 48 kHz y 192 kHz

Aplicación del teorema del muestreo
Un ejemplo donde vemos la utilización del muestreo de señales es en el audio digital, pero
¿Qué es e l audio digital?
Es la representación de una señal de audio mediante números, en general codificados en forma binaria (es decir con ceros y unos).
¿Por qué se utiliza el audio digital?
Porque tiene algunas ventajas sobre el audio analógico que lo hacen insustituible. En primer lugar permite ser almacenado en forma inalterable. Dado que lo que se almacenan son números, es decir símbolos, es mucho mas difícil alterar la información.

Aplicación del teorema del muestreo
Osciloscopios Digitales
Los osciloscopios digitales al igual que los osciloscopios análogos, son instrumentos que permiten visualizar y medir una señal eléctrica, con la diferencia que utilizan la digitalización de la señal de entrada. La digitalización consiste en asignar un código binario a muestras que se toman de la señal de entrada análoga. Estos códigos se ordenan y almacenan secuencialmente de modo que pueda reproducir la señal de entrada en cualquier momento. Para realizar la digitalización se necesita un circuito que obtenga las muestras y un conversor análogo-digital (ADC); para su almacenamiento es necesario una memoria. Después que los datos están almacenados, se pueden hacer diferentes tipos de cálculos realizados por el mismo osciloscopio o asistido por computador.

Aplicación del teorema del muestreo

Ejemplo del teorema de muestreo

Aliasing
El aliasing es un fenómeno propio de la conversión A/D, en el cual la frecuencia de la señal reconstruida es menor que el de la señal original, lo cual ocurre cuando la frecuencia de muestreo es demasiado baja; estos efectospueden reducirse utilizando filtros

CRITERIO DE NYQUIST SHANNON

Ejemplo aplicación del CRITERIO DE NYQUIST SHANNON
se quiere muestrear una señal de la que se sabe se encuentra compuesta por frecuencias entre 12 MHz y 13 Mhz, la aplicación del Teorema general delmuestreo plantearía que la señal debe muestrearse como mínimo a:fs = 2 F máxfs = 2 (13 MHz)fs = 26 MHzFrecuencia que es que es demasiado alta para un muestreo típico.

Ejemplo aplicación del CRITERIO DE NYQUIST SHANNON
Por el contrario, al aplicar el criterio de Nyquist Shannon, sería suficiente con:fs = 2 BWfs = 2 (F máx – F mín)fs = 2 (13 MHz – 12 MHz)fs = 2 MHzFrecuencia de muestreo que puede ser más sencilla de implementar

Cosas que debemos saber…
¿Cómo se elige la cantidad de sub-intervalos en que se divide el rango útil de la señal?
Normalmente se elige como una potencia de 2, de manera que los valores asignados a las muestras están entre 0 y (2^n) – 1, donde n corresponde a la cantidad de bits, es decir de dígitos binarios
¿Qué es la frecuencia de muestreo?
También llamada tasa de muestreo , es la cantidad de muestras por unidad de tiempo. Cuanto mayor sea, mayor es la respuesta en frecuencia del sistema. El estándar para los discos compactos (CD) es de 44,1 kHz.
¿Cómo se elige la frecuencia de muestreo?
Debe ser mayor que el doble de la máxima frecuencia fmáx presente en la señal. Esta condición se denomina condición de Nyquist. Obsérvese que no es suficiente que sea mayor que el doble de la máxima frecuencia útil, ya que si hay ruido por encima de ésta, podría producirse un tipo de distorsión denominado aliasing









Conclusión
El teorema del muestreo para funciones tipo pasabajos es vital en la ingeniería de comunicaciones, vinculando las señales continuas con las discretas.
Los distintos nombres que el teorema ha recibido –Shannon, Nyquist, Kotelnikov, Whittaker, Someya, etc.– indica la independencia de los diferentes enfoques.
Esta historia también pone de manifiesto un proceso muchas veces aparente en los problemas teóricos en física o tecnología: en primer lugar los experimentadores establecen un conjunto de reglas empíricas, luego los teóricos desarrollan la solución general, y finalmente alguien descubre que los matemáticos habían resuelto el problema matemático subyacente con anterioridad, pero en “magnífica soledad”.